LeetCode笔记：反转链表专题

LeetCode笔记：反转链表专题

自大学开始，我便陆陆续续的学习一些 算法和数据结构 方面的内容，同时也开始在一些平台刷题，也会参加一些大大小小的算法竞赛。但是平时刷题缺少目的性、系统性，最终导致算法方面进步缓慢。最终，为了自己的未来，我决定开始在LeetCode上进行系统的学习和练习，同时将刷题的轨迹整理记录，分享出来与大家共勉。

---

参考资料： labuladong：递归反转链表：如何拆解复杂问题

参考资料： LeetCode社区官方提供的思路/题解 以及 评论区/题解区各路大神提供的思路/答案

---

一、反转整个链表

206. 反转链表

难度：简单

反转一个单链表。

示例:

输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL

进阶: 你可以迭代或递归地反转链表。你能否用两种方法解决这道题？

迭代反转链表

方法一：迭代

假设链表为 1→2→3→∅，我们想要把它改成∅←1←2←3。

在遍历链表时，将当前节点的 next 指针改为指向前一个节点。由于节点没有引用其前一个节点，因此必须事先存储其前一个节点。在更改引用之前，还需要存储后一个节点。最后返回新的头引用。

class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode prev = null;
        ListNode curr = head;
        while (curr != null) {
            ListNode next = curr.next;
            curr.next = prev;
            prev = curr;
            curr = next;
        }
        return prev;
    }
}

复杂度分析

时间复杂度：O(n)，其中 nn 是链表的长度。需要遍历链表一次。

空间复杂度：O(1)。

递归反转链表

方法二：递归

这个算法可能很多读者都听说过，这里详细介绍一下，先直接看实现代码：

class Solution {
    public ListNode reverseList(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }
        ListNode newHead = reverseList(head.next);
        head.next.next = head;
        head.next = null;
        return newHead;
    }
}

复杂度分析

时间复杂度：O(n)，其中 n 是链表的长度。需要对链表的每个节点进行反转操作。

空间复杂度：O(n)，其中 n 是链表的长度。空间复杂度主要取决于递归调用的栈空间，最多为 n 层。

---

看起来是不是感觉不知所云，完全不能理解这样为什么能够反转链表？这就对了，这个算法常常拿来显示递归的巧妙和优美，我们下面来详细解释一下这段代码。

对于递归算法，最重要的就是明确递归函数的定义。具体来说，我们的 reverse 函数定义是这样的：

输入一个节点 head，将「以 head 为起点」的链表反转，并返回反转之后的头结点。

明白了函数的定义，在来看这个问题。比如说我们想反转这个链表：

那么输入 reverse(head) 后，会在这里进行递归：

ListNode last = reverse(head.next);

不要跳进递归（你的脑袋能压几个栈呀？），而是要根据刚才的函数定义，来弄清楚这段代码会产生什么结果：

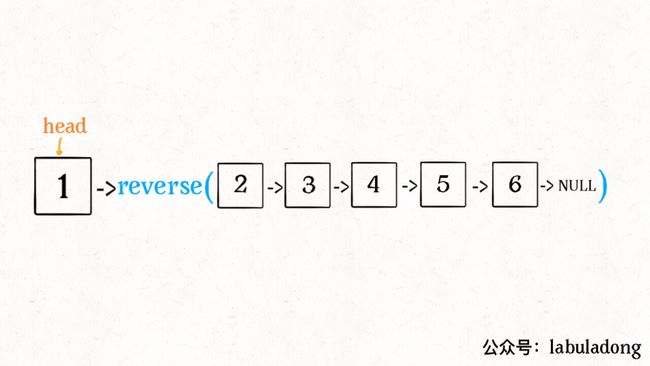
这个 reverse(head.next) 执行完成后，整个链表就成了这样：

并且根据函数定义，reverse 函数会返回反转之后的头结点，我们用变量 last 接收了。

现在再来看下面的代码：

head.next.next = head;

接下来：

head.next = null;
return last;

神不神奇，这样整个链表就反转过来了！递归代码就是这么简洁优雅，不过其中有两个地方需要注意：

1、递归函数要有 base case，也就是这句：

if (head.next == null) return head;

意思是如果链表只有一个节点的时候反转也是它自己，直接返回即可。

2、当链表递归反转之后，新的头结点是 last，而之前的 head 变成了最后一个节点，别忘了链表的末尾要指向 null：

head.next = null;

理解了这两点后，我们就可以进一步深入了，接下来的问题其实都是在这个算法上的扩展。

二、反转链表前 N 个节点

这次我们实现一个这样的函数：

// 将链表的前 n 个节点反转（n <= 链表长度）
ListNode reverseN(ListNode head, int n)

比如说对于下图链表，执行 reverseN(head, 3)：

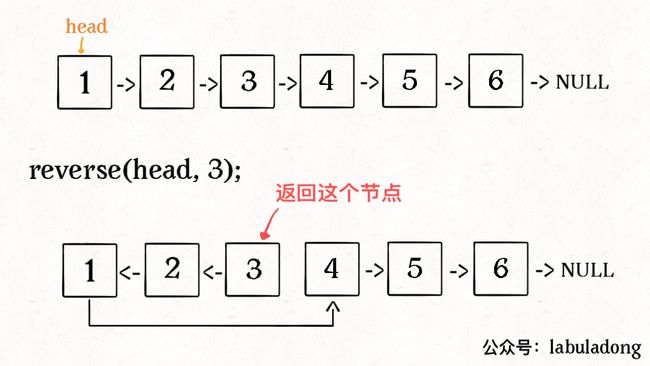
解决思路和反转整个链表差不多，只要稍加修改即可：

ListNode successor = null; // 后驱节点

// 反转以 head 为起点的 n 个节点，返回新的头结点
ListNode reverseN(ListNode head, int n) {
    if (n == 1) { 
        // 记录第 n + 1 个节点
        successor = head.next;
        return head;
    }
    // 以 head.next 为起点，需要反转前 n - 1 个节点
    ListNode last = reverseN(head.next, n - 1);

    head.next.next = head;
    // 让反转之后的 head 节点和后面的节点连起来
    head.next = successor;
    return last;
}

具体的区别：

1、base case 变为 n == 1，反转一个元素，就是它本身，同时要记录后驱节点。

2、刚才我们直接把 head.next 设置为 null，因为整个链表反转后原来的 head 变成了整个链表的最后一个节点。但现在 head 节点在递归反转之后不一定是最后一个节点了，所以要记录后驱 successor（第 n + 1 个节点），反转之后将 head 连接上。

OK，如果这个函数你也能看懂，就离实现「反转一部分链表」不远了。

三、反转链表的一部分

92. 反转链表 II

难度：中等

反转从位置 m 到 n 的链表。请使用一趟扫描完成反转。

说明:
1 ≤ m ≤ n ≤ 链表长度。

示例:

输入: 1->2->3->4->5->NULL, m = 2, n = 4
输出: 1->4->3->2->5->NULL

---

现在解决我们最开始提出的问题，给一个索引区间 [m,n]（索引从 1 开始），仅仅反转区间中的链表元素。

ListNode reverseBetween(ListNode head, int m, int n)

首先，如果 m == 1，就相当于反转链表开头的 n 个元素嘛，也就是我们刚才实现的功能：

ListNode reverseBetween(ListNode head, int m, int n) {
    // base case
    if (m == 1) {
        // 相当于反转前 n 个元素
        return reverseN(head, n);
    }
    // ...
}

如果 m != 1 怎么办？如果我们把 head 的索引视为 1，那么我们是想从第 m 个元素开始反转对吧；如果把 head.next 的索引视为 1 呢？那么相对于 head.next，反转的区间应该是从第 m - 1 个元素开始的；那么对于 head.next.next 呢……

区别于迭代思想，这就是递归思想，所以我们可以完成代码：

ListNode reverseBetween(ListNode head, int m, int n) {
    // base case
    if (m == 1) {
        return reverseN(head, n);
    }
    // 前进到反转的起点触发 base case
    head.next = reverseBetween(head.next, m - 1, n - 1);
    return head;
}

至此，我们的最终大 BOSS 就被解决了。

附：完整代码–Java

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseBetween(ListNode head, int m, int n) {
        // base case
        if (m == 1) {
            return reverseN(head, n);
        }
        // 前进到反转的起点触发 base case
        head.next = reverseBetween(head.next, m - 1, n - 1);
        return head;
    }

    
    ListNode successor = null; // 后驱节点
    // 反转以 head 为起点的 n 个节点，返回新的头结点
    ListNode reverseN(ListNode head, int n) {
        if (n == 1) {
            // 记录第 n + 1 个节点
            successor = head.next;
            return head;
        }
        // 以 head.next 为起点，需要反转前 n - 1 个节点
        ListNode last = reverseN(head.next, n - 1);

        head.next.next = head;
        // 让反转之后的 head 节点和后面的节点连起来
        head.next = successor;
        return last;
    }
}

四、最后总结

递归的思想相对迭代思想，稍微有点难以理解，处理的技巧是：不要跳进递归，而是利用明确的定义来实现算法逻辑。

处理看起来比较困难的问题，可以尝试化整为零，把一些简单的解法进行修改，解决困难的问题。

值得一提的是，递归操作链表并不高效。和迭代解法相比，虽然时间复杂度都是 O(N)，但是迭代解法的空间复杂度是 O(1)，而递归解法需要堆栈，空间复杂度是 O(N)。所以递归操作链表可以作为对递归算法的练习或者拿去和小伙伴装逼，但是考虑效率的话还是使用迭代算法更好。