十大排序算法之堆排序

堆排序

在简单选择排序文章中，简单选择排序这个“铁憨憨”只顾着自己做比较，并没有将对比较结果进行保存，因此只能一遍遍地重复相同的比较操作，降低了效率。针对这样的操作，Robertw.Floyd 在1964年提出了简单选择排序的升级版——堆排序方法。
堆是什么呢？堆是用数组实现的已标号的完全二叉树。

1. 算法思想

在讲算法思想前，先解释几个基本知识点。就像上文所说的：用数组实现的已标号的完全二双树称之为堆。如果父节点的键值均不小于子节点，则为大顶堆；如果父节点的键值均不大于子节点，则为小顶堆，如下图所示。

圆圈旁边的数字即为节点的索引，如果我们按照这个索引将节点的逻辑结构映射到数组中，就变成了如下图所示的存储结构。

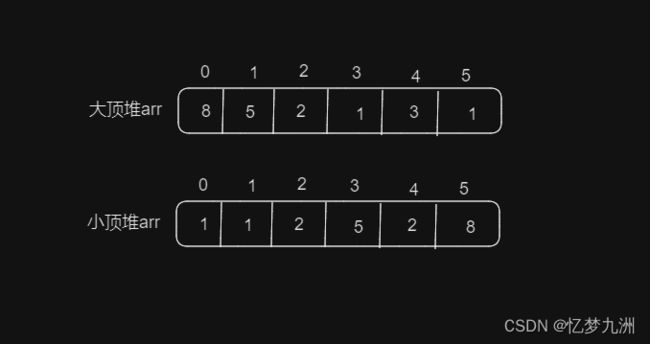
我们再用两个公式简单地描述一下节点之间的关系。
大顶堆：$arr[i]\ge arr[2i+1]$ && $arr[i]\le arr[2i+2]$
小顶堆：$arr[i]\le arr[2i+1]$ && $arr[i]\ge arr[2i+2]$
如果大家看懂了这两个公式，那么就会理解堆排序的基本思想：一次又一次地将待排序数组构造成一个大顶堆，然后一次又一次地将大顶堆的根节点（最大值）和最末尾的元素交换位置并将最末尾的元素隔离，直到整个序列变得有序。

2. 算法步骤

假设初始序列的堆结构如下图所示。

（1）将待排序数组构建成一个大顶堆（若降序排列，则采用小顶堆）。
为了构建大顶堆，我们需要从最后一个非叶子节点开始先从左到右，再从上到下地进行调整。最后一个非叶子节点的计算公式为：
$$\frac{arr.length}{2}-1=\frac{6}{2}-1=2$$
即为“2”节点，由于8>2，所以将二者交换，如下图所示。

找到第二个非叶子节点“5”，因为［5，1,3］中5最大，所以无须进行交换。第三个非叶子节点为“1”，因为［1，5，8］中8最大，所以1和8交换，如下图所示。
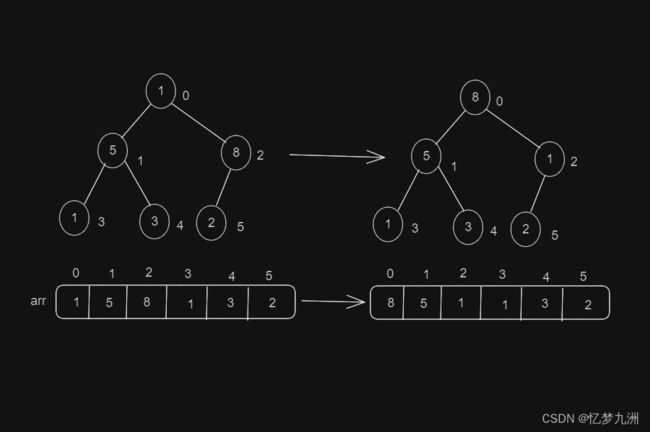我们发现，这次交换后右子树又被打乱了，2比1大，因此需要再更新一下，如下图所示。

这样，我们成功地将待排序数组构建成第一个大顶堆。

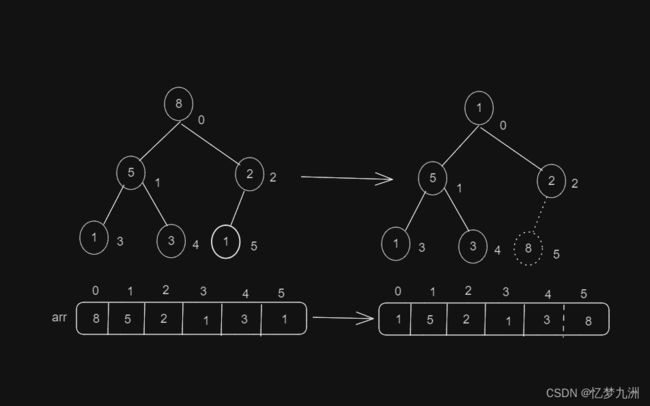
（3）重复步骤（1）和（2），直到整个序列变得有序。
重新调整数组结构，使其满足大顶堆的结构，如下图所示。

然后继续交换堆顶和堆底的元素，又“沉”了一个，如下图所示。

接下来都是类似操作，就这样一直执行，直到整个数组变得有序，如下图所示。

3. 算法分析

有的读者肯定有疑问，为什么在经过步骤（1）和步骤（2），进行了四五次比较和交换的操作后，得到的有序数组意然和开始的待排序数组是一样的，都是［1，5,2,1,3，8］呢？其实这也是堆排序的一个不足之处。那么我们如何最大化地提升堆排序的效率呢？这个问题就交给大家去思考吧。
堆排序的思想总结起来有两点：构建堆结构+交换堆顶和堆底元素。构建第一个大顶堆时，时间复杂度为O(n)之后还有n-1次的交换元素和交换之后堆的重建，根据完全二叉树的性质来说，操作次数应该是呈$log(n-1),log(n-2),log(n-3),\cdots ,1$的态势逐步递减的，也就近似为$O(lo{g}_{2}n)$。因此，不难得出，堆排序的时间复杂度为$O(nlogn)$。
同样，当待排序数组是逆序时，就是最坏的情况。这时候不仅需要进行$O(nlogn)$复杂度的比较操作，还需要进行$O(nlogn)$复杂度的交顿操作，加起来总的时间复杂度为$O(nlogn)$。
最好的情况则是正序的时候，只需要进行$O(nlogn)$复杂度的比较操作，而不需移动操作，不过总的时间复杂度还是$O(nlogn)$。也就是说，待排序数据的原始分布情况对堆排序的效率影响是比较小的。
另外，堆排序也是不稳定排序。

4. 算法代码

算法代码如下：
Pyhton

#堆排序
def heap_sort(array) :
    """
    这里需要注意两点：
    （1）递归思想（2）列表切片
    """
    length = len(array)
    #当数组 array 的长度为1时，说明只有一个元素
    if length<= 1:
        #无须排序，直接返回原列表
        return array
    # 若存在两个或以上节点
    else:
        #调整成大顶堆：按照先从下往上，再从左到右的顺序进行调整
        # 从最后一个非叶子节点（length//2-1）开始向前遍历，直到根节点
        for i in range(length//2-1,-1,-1):# //为取整
            # 当左孩儿大于父节点时
            if array[2*i+1] > array[i]:
                #二者交換位置
                array[2*i+1],array[i]=array[i],array[2*i+1] # 如果右孩儿存在且大于父节点时
            if 2*i+2 <= length-1:
                if array[2*i+2]> array[i]:
                    #二者交換位置
                    array[2*i+2],array[i] = array[i], array[2*i+2]
            '''此处省略重构建过程，对结果并不影响！'''
            # 将堆顶元素与末尾元素进行交换，使最大元素“沉”到数组末尾
        array[0],array[length-1] = array[length-1], array[0]
        #递归调用 heap_sort函数对前n-1个元素进行堆排序并返回排序后的结果
    return heap_sort(array [0:length-1]) + array[length-1:]
# 调用 heapsort 函数
print(heap_sort([34, 21, 13, 2, 5, 1, 55, 3, 1, 8]))

Java

    public static int[] heap_sort(int[] array) {
        int length = array.length;
        if (length <= 1) {
            return array;
        } else {
            // 构建最大堆
            for (int i = length / 2 - 1; i >= 0; i--) {
                maxHeapify(array, i, length);
            }

            // 交换堆顶元素与末尾元素并减小堆大小
            for (int end = length - 1; end > 0; end--) {
                swap(array, 0, end);
                length--;
                maxHeapify(array, 0, length); // 调整堆
            }
        }

        return array;
    }



    private static void maxHeapify(int[] array, int i, int size) {
        int left = 2 * i + 1;
        int right = 2 * i + 2;
        int largest = i;

        if (left < size && array[left] > array[largest]) {
            largest = left;
        }
        if (right < size && array[right] > array[largest]) {
            largest = right;
        }

        if (largest != i) {
            swap(array, i, largest);
            maxHeapify(array, largest, size);
        }
    }

    private static void swap(int[] array, int i, int j) {
        int temp = array[i];
        array[i] = array[j];
        array[j] = temp;
    }
        @Test
        void contextLoads () {
            int[] array={34, 21, 13, 2, 5, 1, 55, 3, 1, 8};
            System.out.println(Arrays.toString(heap_sort(array)));
        }

5. 输出结果

6. 算法过程分解

第1次递归
待排序数组如下：
[34, 21, 13, 2, 5, 1, 55, 3, 1, 8]
第1次返回结果：[1, 1, 2, 3, 5, 8, 13, 21, 34]+[55]
第2次递归
待排序数组如下：
[5, 21, 34, 3, 8, 1, 13, 2, 1]
第2次返回结果：[1, 1, 2, 3, 5, 8, 13, 21]+[34]
第3次递归
待排序数组如下：
[1, 5, 21, 3, 8, 1, 13, 2]
第3次返回结果：[1, 1, 2, 3, 5, 8, 13]+[21]
第4次递归
待排序数组如下：
[2, 1, 8, 3, 5, 1, 13]
第4次返回结果：[1, 1, 2, 3, 5, 8]+[13]
第5次递归
待排序数组如下：
[8, 2, 5, 1, 3, 1]
第5次返回结果：[1, 1, 2, 3, 5]+[8]
第6次递归
待排序数组如下：
[1, 3, 5, 1, 2]
第6次返回结果：[1, 1, 2, 3]+[5]
第7次递归
待排序数组如下：
[2, 1, 3, 1]
第7次返回结果：[1, 1, 2]+[3]
第8次递归
待排序数组如下：
[1, 1, 2]
第8次返回结果：[1, 1]+[2]
第9次递归
待排序数组如下：
[1, 1]
第9次返回结果：[1]+[1]
第10次递归
待排序数组如下：
[1]
因为只有一个元素，所以无须排序
第10次返回结果：[1]