AcWing算法学习笔记:基础算法(快速排序 + 归并排序 + 二分 + 高精度 +前缀和差分 + 双指针算法 + 位运算 + 离散化 + 区间和并)
基础算法
- 一、快速排序
-
- ①快速排序⭐
- ②第k个数
- 二、归并排序
-
- ①归并排序
- ②逆序对的数量⭐
- 三、二分
-
- ①数的范围⭐
- ②数的三次方根⭐
- 四、高精度
-
- ①高精度加法
- ②高精度减法
- ③高精度乘法
- ④高精度除法
- 五、前缀和差分
-
- ①前缀和
- ②子矩阵的和
- ③差分
- ④差分矩阵
- 六、双指针算法
-
- ①最长连续不重复子序列
- ②数组元素的目标和
- ③判断子序列
- 七、位运算(二进制数中1的个数)⭐
- 八、离散化( 区间和)⭐
- 九、区间合并
一、快速排序
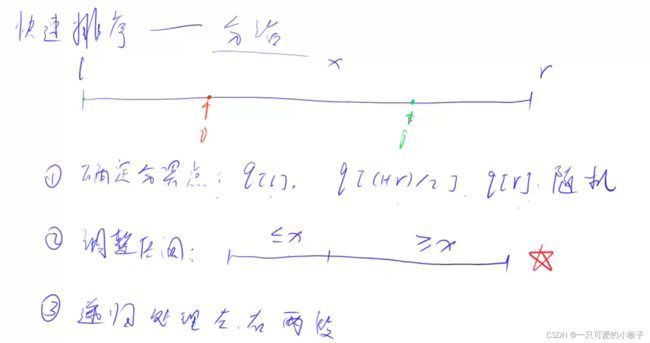
①快速排序⭐
- 优美做法
使用i, j 两个指针,当a[i] < x,i ++; 当a[j] > x, j –
当i和j都无法移动时,swap(a[i], a[j]) - 暴力做法
遍历一遍数组,将小于x的放入a数组,将大于x的放入b数组
最后将a数组和b数组的数移动到a数组中
上述两种方法均能实现数组a分为两部分
时间复杂度
0(nlogn)
递归logn层,每层0(n)
代码
#include ②第k个数
算法
快排算法的简单应用
在递归左右区间时,根据第k个数在哪个区间进行递归
递归时,更新在该区间中那个目标值在区间中的位置
代码
#include 二、归并排序
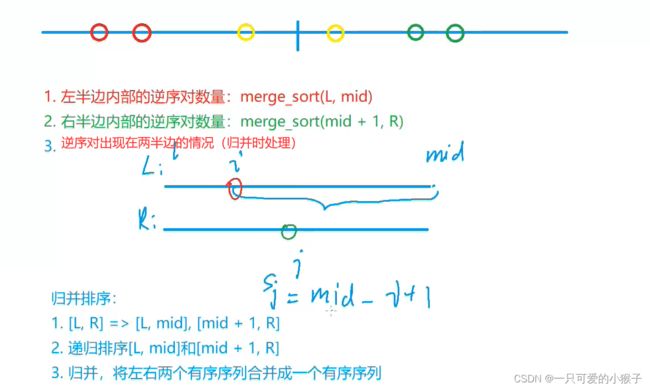
①归并排序
算法

递归排序后,左右两个区间均为 有序序列
再使用双指针将两个序列合并为一个序列
时间复杂度
递归0(logn)层
每一层遍历0(n)
总的时间复杂度为0(nlogn)
代码
#include ②逆序对的数量⭐
代码
#include 三、二分
①数的范围⭐
算法
利用某种性质,使数组一分为二,不断缩小区间,最后找到性质的边界范围
将数组a[N]根据某种性质划分为两部分
根据mid值所在的区间进行边界的判定
如果想要得到红色边界
当mid在红色边界内时,缩小L,L = mid
反之 缩小R, R = mid - 1
如果想要得到绿色边界
当mid在绿色边界内时,缩小R, R = mid
反之,缩小L, L = mid + 1
代码
#include ②数的三次方根⭐
算法
与整数二分类似
浮点数的二分,边界无需加一,只需要根据mid所在的区域,更新L/R为mid即可
代码
#include 四、高精度
①高精度加法
算法
A + B (A和B是两个大整数,位数可以是1e6)

然后根据加法从低位逐位相加,并处理进位即可
代码
#include ②高精度减法
算法
A - B (A和B是两个大整数,位数可以是1e6)
如果A >= B 则计算 A - B
如果A < B 则计算 - (B - A)
也是使用数组进行逆序
按照减法逐位相减,处理借位
注意去除前导0,至少保留一个0
代码
#include ③高精度乘法
算法
A * a (大整数A 和 小整数a相乘,A位数为1e6,a数值为1e9)

代码
#include ④高精度除法
算法
A ➗ a (大整数A 和 小整数a相乘,A位数为1e6,a数值为1e9)

就是模拟除法的过程
代码
#include 五、前缀和差分
①前缀和
代码
#include ②子矩阵的和
代码
#include ③差分
代码
#include ④差分矩阵
代码
#include 六、双指针算法
①最长连续不重复子序列
算法

该题使用 j ~ i表示选中的区间
i右移,使用s数组记录选中的数,当选中区间中有重复数字出现时,j右移,当选中区间没有重复数字时j停止移动
区间的长度为i - j + 1
代码
#include ②数组元素的目标和
算法
由于两个数组均是有序递增
因此i只需要从小到大不断右移
如果a[i] + b[j] > x ,则不断左移j,当j停止移动时,a[i] + b[j] 只有可能等于或小于x ,如果是小于,再右移i,增大a[i]即可。
代码
#include ③判断子序列
算法
遍历一遍b数组,如果能够顺次找到a中的每一个数字,则存在子序列
代码
#include 七、位运算(二进制数中1的个数)⭐
代码
#include 八、离散化( 区间和)⭐
代码
#include 九、区间合并
算法
将所有区间按照左端点从小到大进行排序
依次遍历所有区间
如果该区间的左端点大于前面总区间的右端点最大值,则res ++
每次都要更新右端点的最大位置
代码
#include