数字图像处理 阮秋琦 期末复习 #1 绪论及正交变换
考试范围:
- 第三章 图像处理中的正交变换
- 第四章 图像增强
- 第五章 图像编码
- 第六章 图像复原
- 第八章 图像分析
绪论
图像是一种数据结构,笼统来说是一个二维矩阵,每一个点的信息共同组成了视觉平面
数字图像处理的方法
根据上文,数字图像处理的第一种方案是空域法,因为它们是在图像的空间域(spatial domain)中操作的。空域是指图像的像素空间,也就是图像中每个像素的位置和像素值的空间布局。因此,空域法是直接在图像的原始表示中进行操作的方法。
具体来说包括:
- 点处理法(Point Processing)是对图像中的每个像素进行独立的操作,而不考虑像素周围的上下文,有灰度调整、直方图均衡化、颜色调整等。
- 邻域处理法(Neighborhood Processing)邻域处理法涉及到像素周围的像素值,通常使用滤波器或卷积核进行操作。有平滑滤波、锐化滤波、中值滤波、边缘检测等。
注意到,上述研究方法是一种离散和拆分的视角,如果把图像看作整体的对象,研究它具有什么样的特征和成分,则出现了第二种方案即频域法:
- 首先对图像进行正交变换,得到变换域系数阵列, 然后再施行各种处理,处理后再反变换到空间域,得到处理结果。包括:滤波、数据压缩、特征提取等。
第三章 正交变换
为什么采用正交变换?
因为正交性保证了不同频率成分之间是相互独立的,将图像从时域转到频域的过程中也就完成了分析。同时保证信号的总能量不变、易于进行逆变换。
具体来说,对于傅里叶变换
F ( ω ) = ∫ f ( t ) e − j ω t d t F(\omega)=\int f(t)e^{-j\omega t} dt F(ω)=∫f(t)e−jωtdt
有:
∫ e − j ω 1 t e j ω 2 t d t = 2 π δ ( ω 1 − ω 2 ) \int e^{-j\omega_1 t}e^{j\omega_2 t} dt = 2\pi \delta(\omega_1 - \omega_2) ∫e−jω1tejω2tdt=2πδ(ω1−ω2)
若 ω 1 = ω 2 \omega_1 = \omega_2 ω1=ω2则整体为1,若不相等(频率不一致)则该项化为0
对于沃尔什变换
则有:
∑ w i ( n ) w j ( n ) = N δ i j \sum w_i(n)w_j(n) = N\delta_{ij} ∑wi(n)wj(n)=Nδij
其中 w i , w j w_i,w_j wi,wj一致时项为1,不一致时化为0
3.1 傅里叶变换
3.1.1 傅里叶变换性质
- 可分性:二维傅里叶变换可由两重一维傅里叶变换实现: F ( u , v ) = ∫ ∫ f ( x , y ) e − j ω 1 x e − j ω 2 d x d y F(u,v)=\int \int f(x,y)e^{-j\omega_1 x}e^{-j\omega_2}dxdy F(u,v)=∫∫f(x,y)e−jω1xe−jω2dxdy F ( u , v ) = ∫ [ ∫ f ( x , y ) e − j ω 1 x d x ] e − j ω 2 y d y F(u,v)=\int [\int f(x,y)e^{-j\omega_1 x}dx]e^{-j\omega_2 y}dy F(u,v)=∫[∫f(x,y)e−jω1xdx]e−jω2ydy F ( u , v ) = ∫ F x [ f ( x , y ) ] ⋅ e − j ω 2 y d y F(u,v)=\int\mathcal{F}_x[f(x,y)]\cdot e^{-j\omega_2 y}dy F(u,v)=∫Fx[f(x,y)]⋅e−jω2ydy F ( u , v ) = F y [ F x f ( x , y ) ] F(u,v)=\mathcal{F}_y [\mathcal{F}_x f(x,y)] F(u,v)=Fy[Fxf(x,y)] ( 2 π u , 2 π v ) = ( ω 1 , ω 2 ) (2\pi u, 2\pi v )=(\omega_1,\omega_2) (2πu,2πv)=(ω1,ω2)
- 线性性: F [ a f ( x , y ) + b g ( x , y ) ] \mathcal{F}[af(x,y) + bg(x,y)] F[af(x,y)+bg(x,y)] = a F [ f ( x , y ) ] + b F [ g ( x , y ) ] =a\mathcal{F}[f(x,y)] + b\mathcal{F}[g(x,y)] =aF[f(x,y)]+bF[g(x,y)]
- 共轭对称性: F ( u , v ) = F ∗ ( − u , − v ) F(u,v) = F^*(-u,-v) F(u,v)=F∗(−u,−v)
- 旋转性:信号在时域中的移位,将导致傅里叶变换中的相位旋转。 f ( r , θ + θ 0 ) ⇔ F ( k , ϕ + θ 0 ) f(r, \theta + \theta_0) \Leftrightarrow F(k, \phi + \theta_0) f(r,θ+θ0)⇔F(k,ϕ+θ0)
- 比例变换性质: a f ( x , y ) ⇔ a F ( u , v ) af(x,y)\Leftrightarrow aF(u, v) af(x,y)⇔aF(u,v) f ( a x , b y ) ⇔ 1 ∣ a b ∣ F ( u a , v b ) f(ax, by) \Leftrightarrow \frac{1}{|ab|}F(\frac{u}{a},\frac{v}{b}) f(ax,by)⇔∣ab∣1F(au,bv)
- 帕斯维尔定理:变换前后不损失能量 ∫ − ∞ ∞ ∫ − ∞ ∞ ∣ f ( x , y ) ∣ 2 d x d y = ∫ − ∞ ∞ ∫ − ∞ ∞ ∣ F ( u , v ) ∣ 2 d u d v \int\limits_{-\infin}^{\infin}\int\limits_{-\infin}^{\infin}|f(x,y)|^2dxdy=\int\limits_{-\infin}^{\infin}\int\limits_{-\infin}^{\infin}|F(u,v)|^2dudv −∞∫∞−∞∫∞∣f(x,y)∣2dxdy=−∞∫∞−∞∫∞∣F(u,v)∣2dudv
- 相关定理: 没看懂 没看懂 没看懂
- 卷积定理:两个信号在时域中的卷积等于它们在频域中的傅里叶变换的乘积。 ∫ ∫ f ( α , β ) g ( x − α , y − β ) d α d β = f ( x , y ) ∗ g ( x , y ) = F ( u , v ) ⋅ G ( u , v ) \int \int f(\alpha ,\beta)g(x-\alpha,y-\beta)d\alpha d\beta=f(x,y)*g(x,y)=F(u,v)\cdot G(u,v) ∫∫f(α,β)g(x−α,y−β)dαdβ=f(x,y)∗g(x,y)=F(u,v)⋅G(u,v)
3.1.2 离散傅里叶变换
离散傅里叶变换(Discrete Fourier Transform,DFT)是傅里叶变换的一种形式,用于将离散信号(图像)从时域转换到频域。
假设有一个长度为 N N N的离散信号序列 x [ n ] x[n] x[n],其中 n = 0 , 1 , 2 , … , N − 1 n=0,1,2,\dots ,N-1 n=0,1,2,…,N−1,离散傅里叶定义如下: X [ k ] = ∑ n = 0 N − 1 x [ n ] ⋅ e − j 2 π k n N X[k] = \sum\limits_{n=0}^{N-1} x[n]\cdot e^{-j\frac{2\pi kn}{N}} X[k]=n=0∑N−1x[n]⋅e−jN2πkn
其中 k = 0 , 1 , 2 , … , N − 1 k=0,1,2,\dots ,N-1 k=0,1,2,…,N−1表示频域中的离散频率
逆变换表示为: X − 1 ( k ) = x [ n ] = 1 N ∑ k = 0 N − 1 X [ k ] ⋅ e j 2 π k n N X^{-1}(k)=x[n]=\frac{1}{N}\sum\limits_{k=0}^{N-1}X[k]\cdot e^{j\frac{2\pi kn}{N}} X−1(k)=x[n]=N1k=0∑N−1X[k]⋅ejN2πkn
- 线性性: a x ( n ) + b y ( n ) ⇔ a X ( m ) + b Y ( m ) ax(n)+by(n)\Leftrightarrow aX(m) + bY(m) ax(n)+by(n)⇔aX(m)+bY(m)
- 对称性: 1 N X ( n ) ⇔ x ( − m ) \frac{1}{N}X(n)\Leftrightarrow x(-m) N1X(n)⇔x(−m)
- 时间移位: x ( n − k ) = X ( m ) ⋅ e − j 2 π N k m x(n-k)=X(m)\cdot e^{-j\frac{2\pi}{N}km} x(n−k)=X(m)⋅e−jN2πkm
- 频率移位: X ( m − k ) = x ( n ) ⋅ e − j 2 π N ( − k n ) X(m-k)=x(n)\cdot e^{-j\frac{2\pi}{N}(-kn)} X(m−k)=x(n)⋅e−jN2π(−kn)
- 卷积定理: x ( n ) ∗ y ( n ) = X ( M ) ⋅ Y ( M ) x(n)*y(n)=X(M)\cdot Y(M) x(n)∗y(n)=X(M)⋅Y(M) X ( M ) ∗ Y ( M ) = x ( n ) ⋅ y ( n ) X(M)*Y(M) = x(n)\cdot y(n) X(M)∗Y(M)=x(n)⋅y(n)
- 帕斯维尔定理: ∑ n = 0 N − 1 x 2 ( n ) = 1 N ∑ m = 0 N − 1 ∣ X ( m ) ∣ 2 \sum\limits_{n=0}^{N-1}x^2(n) = \frac{1}{N}\sum\limits_{m=0}^{N-1}|X(m)|^2 n=0∑N−1x2(n)=N1m=0∑N−1∣X(m)∣2 (用 ∑ n = 0 N − 1 \sum\limits_{n=0}^{N-1} n=0∑N−1代替 ∫ d x \int dx ∫dx)
3.1.3 快速傅里叶变换
快速傅里叶变换并不是一种新的变换,它是离散傅里叶变换的一种算法。这种方法利用傅里叶变换的对称性和周期性,通过将 DFT 分解为多个规模较小的 DFT消除了离散傅里叶的多余运算,时间复杂度为 O ( N l o g N ) O(NlogN) O(NlogN),在某些应用场合已能作到实时处理。
对于离散傅里叶变换: x ( n ) = 1 N ∑ n = 0 N − 1 X ( m ) ⋅ e − j 2 π N − > m n x(n)=\frac{1}{N}\sum\limits_{n=0}^{N-1}X(m)\cdot e^{-j\frac{2\pi}{N}-> mn} x(n)=N1n=0∑N−1X(m)⋅e−jN2π−>mn X ( m ) = ∑ n = 0 N − 1 x ( n ) ⋅ e − j 2 π N m n X(m)=\sum\limits_{n=0}^{N-1}x(n)\cdot e^{-j\frac{2\pi}{N}mn} X(m)=n=0∑N−1x(n)⋅e−jN2πmn
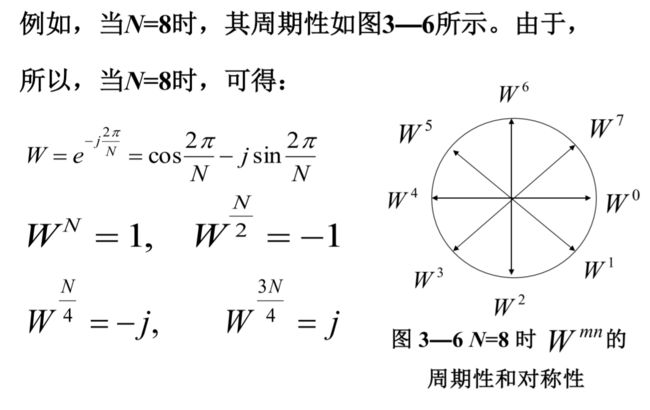
以 W = e − j 2 π N W=e^{-j\frac{2\pi}{N}} W=e−jN2π展开得到
X ( 0 ) = x ( n = 0 ) W 0 ∗ n = 0 + x ( n = 1 ) W 0 ∗ n = 1 + ⋯ + x ( N − 1 ) W 0 ( N − 1 ) X(0) = x(n=0)W^{0*n=0} + x(n=1)W^{0*n=1}+\dots +x(N-1)W^{0(N-1)} X(0)=x(n=0)W0∗n=0+x(n=1)W0∗n=1+⋯+x(N−1)W0(N−1)
X ( 1 ) = x ( n = 0 ) W 1 ∗ n = 0 + x ( n = 1 ) W 1 ∗ n = 1 + ⋯ + x ( N − 1 ) W 1 ( N − 1 ) X(1) = x(n=0)W^{1*n=0} + x(n=1)W^{1*n=1}+\dots +x(N-1)W^{1(N-1)} X(1)=x(n=0)W1∗n=0+x(n=1)W1∗n=1+⋯+x(N−1)W1(N−1)
X ( 2 ) = x ( n = 0 ) W 2 ∗ n = 0 + x ( n = 1 ) W 2 ∗ n = 1 + ⋯ + x ( N − 1 ) W 2 ( N − 1 ) X(2) = x(n=0)W^{2*n=0} + x(n=1)W^{2*n=1}+\dots +x(N-1)W^{2(N-1)} X(2)=x(n=0)W2∗n=0+x(n=1)W2∗n=1+⋯+x(N−1)W2(N−1)
… \dots …
X ( N − 1 ) = x ( n = 0 ) W ( N − 1 ) ∗ n = 0 + x ( n = 1 ) W ( N − 1 ) ∗ n = 1 + ⋯ + x ( N − 1 ) W ( N − 1 ) ∗ ( N − 1 ) X(N-1) = x(n=0)W^{(N-1)*n=0} + x(n=1)W^{(N-1)*n=1}+\dots +x(N-1)W^{(N-1)*(N-1)} X(N−1)=x(n=0)W(N−1)∗n=0+x(n=1)W(N−1)∗n=1+⋯+x(N−1)W(N−1)∗(N−1)
要完成DFT,需要 N 2 N^2 N2次乘法和 N ( N − 1 ) N(N-1) N(N−1)次加法
对于 W N m = e − j 2 π N m W^{m}_N = e^{-j\frac{2\pi}{N}m} WNm=e−jN2πm,因有 W N m = W 2 N 2 m (偶), W N m + N 2 = − W N m (奇) W^m_N = W^{2m}_{2N}(偶),W^{m+\frac{N}{2}}_N = -W^m_N(奇) WNm=W2N2m(偶),WNm+2N=−WNm(奇)可以进行化简:
- 按时间分解:
把 x ( n ) x(n) x(n)分成偶数点和奇数点,有
x 1 ( n ) = x ( n ) x_1(n)=x(n) x1(n)=x(n)
x 2 ( n ) = x ( 2 n + 1 ) x_2(n)=x(2n+1) x2(n)=x(2n+1)
得到算法流程图:
- 按频率分解:
把 x ( n ) x(n) x(n)分成偶数点和奇数点,即:
x 1 ( n ) = x ( 2 n ) x_1(n)=x(2n) x1(n)=x(2n)
x 2 ( n ) = x ( 2 n + 1 ) x_2(n)=x(2n+1) x2(n)=x(2n+1)
得到算法流程图:
3.2 沃尔什变换
FFT需要用到复数乘法,运算负担较大,因此引入了更快的沃尔什变换。
3.2.1 沃尔什函数
沃尔什(Walsh)函数集是完备的非正弦型的二元(取值为+1与-1)正交函数集,沃尔什函数是定义在半开区间 [0,1) 的矩形波族, 每个矩形波有一个编号 n ( n = 0 , 1 , 2 , 3 , … ) n(n = 0 , 1 , 2 , 3 , … ) n(n=0,1,2,3,…),,满足封闭性,构成群。

按沃尔什排列的沃尔什函数表达式为: w a l ( i , t ) = ∏ k = 0 P − 1 [ R ( k + 1 , t ) ] g ( i ) k , g ( i ) ∈ 0 , 1 wal(i,t)=\prod\limits_{k=0}^{P-1}[R(k+1,t)]^{g(i)_k},g(i)\in {0,1} wal(i,t)=k=0∏P−1[R(k+1,t)]g(i)k,g(i)∈0,1
沃尔什函数的性质:
- 在区间 [ 0 , 1 ] [0, 1] [0,1]有 ∫ 0 1 w a l ( 0 , t ) d t = 1 \int\limits^1_0 wal(0,t)dt=1 0∫1wal(0,t)dt=1 ∫ 0 1 w a l ( i , t ) d t = 0 , i > 0 \int\limits_0^1 wal(i,t)dt=0, i>0 0∫1wal(i,t)dt=0,i>0 [ w a l ( i , t ) ] 2 = 1 , i = 0 , 1 , 2 , 3 , … [wal(i,t)]^2=1, i=0,1,2,3,\dots [wal(i,t)]2=1,i=0,1,2,3,…
- 在第一小段时间内总是取 + 1 +1 +1
- 乘法定理(服从结合律): w a l ( i , t ) ⋅ w a l ( j , t ) = w a l ( i ⊕ j , t ) wal(i,t)\cdot wal(j,t) = wal(i\oplus j, t) wal(i,t)⋅wal(j,t)=wal(i⊕j,t) 其中 ⊕ \oplus ⊕为模二加法
- 沃尔什函数有归一化正交性: ∫ 0 1 w a l ( i , t ) ⋅ w a l ( j , t ) d t = { 0 , i ≠ j 1 , i = j \int\limits_0^1 wal(i,t)\cdot wal(j,t)dt=\begin{cases} 0,&\text i\neq j\\ 1,&\text i=j \end{cases} 0∫1wal(i,t)⋅wal(j,t)dt={0,1,i=ji=j
3.2.2 离散沃尔什变换
离散沃尔什变换的表达式为: W ( i ) = 1 N ∑ t = 0 N − 1 f ( t ) ⋅ w a l ( i , t ) W(i)=\frac{1}{N}\sum\limits_{t=0}^{N-1}f(t)\cdot wal(i,t) W(i)=N1t=0∑N−1f(t)⋅wal(i,t) f ( t ) = ∑ i = 0 N − 1 W ( i ) ⋅ w a l ( i , t ) f(t)=\sum\limits_{i=0}^{N-1}W(i)\cdot wal(i,t) f(t)=i=0∑N−1W(i)⋅wal(i,t)
离散沃尔什-哈达玛变换的表现形式如下:
[ W ( 0 ) W ( 1 ) ⋮ W ( N − 1 ) ] = 1 N [ H ( N ) ] [ f ( 0 ) f ( 1 ) ⋮ f ( N − 1 ) ] \begin{bmatrix} W(0) \\ W(1) \\ \vdots \\ W(N-1) \end{bmatrix} =\frac{1}{N}[H(N)]\begin{bmatrix} f(0) \\ f(1) \\ \vdots \\ f(N-1) \end{bmatrix} W(0)W(1)⋮W(N−1) =N1[H(N)] f(0)f(1)⋮f(N−1)

离散沃尔什-哈达玛变换的性质:
- 线性性: a { f 1 ( t ) } + b { f 2 ( t ) } ⇔ a { W 1 ( n ) } + b { W 2 ( n ) } a\{f_1(t)\} + b\{f_2(t)\}\Leftrightarrow a\{W_1(n)\}+b\{W_2(n)\} a{f1(t)}+b{f2(t)}⇔a{W1(n)}+b{W2(n)}
- 模2移位: { z ( m ) } = f ( t ⊕ l ) 是 f ( t ) \{z(m)\}=f(t\oplus l)是f(t) {z(m)}=f(t⊕l)是f(t)的模2移位序列
- 模2移位时间卷积定理: { f 1 ( t ) } , { f 2 ( t ) } \{f_1(t)\},\{f_2(t)\} {f1(t)},{f2(t)}是两个长度相同的周期性序列,则定义两个序列的模2移位卷积: C 12 ( t ) = 1 N ∑ l = 0 N − 1 f 1 ( l ) ⋅ f 2 ( t ⊕ l ) C_{12}(t)=\frac{1}{N}\sum\limits_{l=0}^{N-1}f_1(l)\cdot f_2(t\oplus l) C12(t)=N1l=0∑N−1f1(l)⋅f2(t⊕l) 如果 { f 1 ( t ) } ⇔ { W 1 ( n ) } \{f_1(t)\}\Leftrightarrow \{W_1(n)\} {f1(t)}⇔{W1(n)} { f 2 ( t ) } ⇔ { W 2 ( n ) } \{f_2(t)\}\Leftrightarrow \{W_2(n)\} {f2(t)}⇔{W2(n)} 则可证 { C 12 ( t ) } ⇔ { W 1 ( n ) ⋅ W 2 ( n ) } \{C_{12}(t)\}\Leftrightarrow \{W_1(n)\cdot W_2(n)\} {C12(t)}⇔{W1(n)⋅W2(n)}
3.3 算法考点
3.3.1 计算快速傅里叶变换
3.3.2 证明沃尔什变换模2移位时间卷积定理
证明:
用 W \mathcal{W} W表示沃尔什变换,则
W [ C 12 ( t ) ] = 1 N ∑ t = 0 N − 1 C 12 ⋅ w a l ( n , t ) \mathcal{W}[C_{12}(t)] = \frac{1}{N}\sum\limits_{t=0}^{N-1}C_{12}\cdot wal(n, t) W[C12(t)]=N1t=0∑N−1C12⋅wal(n,t)
= 1 N ∑ t = 0 N − 1 [ 1 N ∑ t = 0 N − 1 f 1 ( l ) ⋅ f 2 ( t ⊕ l ) ] ⋅ w a l ( n , l ) =\frac{1}{N}\sum\limits_{t=0}^{N-1}[\frac{1}{N}\sum\limits_{t=0}^{N-1}f_1(l)\cdot f_2(t\oplus l)]\cdot wal(n,l) =N1t=0∑N−1[N1t=0∑N−1f1(l)⋅f2(t⊕l)]⋅wal(n,l)
= 1 N ∑ t = 0 N − 1 f 1 ( l ) [ 1 N ∑ t = 0 N − 1 f 2 ( t ⊕ l ) ⋅ w a l ( n , t ) ] =\frac{1}{N}\sum\limits_{t=0}^{N-1}f_1(l)[\frac{1}{N}\sum\limits_{t=0}^{N-1}f_2(t\oplus l)\cdot wal(n,t)] =N1t=0∑N−1f1(l)[N1t=0∑N−1f2(t⊕l)⋅wal(n,t)]
= 1 N ∑ t = 0 N − 1 f 1 ⋅ W 2 ( n ) ⋅ w a l ( n , l ) =\frac{1}{N}\sum\limits_{t=0}^{N-1} f_1\cdot W_2(n)\cdot wal(n,l) =N1t=0∑N−1f1⋅W2(n)⋅wal(n,l)
= W 2 ( n ) ⋅ [ 1 N ∑ t = 0 N − 1 f 1 ( l ) ⋅ w a l ( n , l ) ] =W_2(n)\cdot[\frac{1}{N}\sum\limits_{t=0}^{N-1}f_1(l)\cdot wal(n,l)] =W2(n)⋅[N1t=0∑N−1f1(l)⋅wal(n,l)]
= W 2 ( n ) ⋅ W 1 ( n ) =W_2(n)\cdot W_1(n) =W2(n)⋅W1(n)
3.3.3 证明沃尔什函数有归一化正交性
证明:
∫ 0 1 w a l ( i , t ) ⋅ w a l ( j , t ) d t = { 0 , i ≠ j 1 , i = j \int\limits_0^1 wal(i,t)\cdot wal(j,t)dt=\begin{cases} 0,&\text i\neq j\\ 1,&\text i=j \end{cases} 0∫1wal(i,t)⋅wal(j,t)dt={0,1,i=ji=j
由乘法定理有:
∫ 0 1 w a l ( i , t ) ⋅ w a l ( j , t ) d t = ∫ 0 1 w a l ( i ⊕ j , t ) d t \int\limits_0^1 wal(i,t) \cdot wal(j,t) dt=\int\limits_0^1 wal(i\oplus j,t)dt 0∫1wal(i,t)⋅wal(j,t)dt=0∫1wal(i⊕j,t)dt
= ∫ 0 1 w a l ( l , t ) d t =\int\limits_0^1 wal(l,t)dt =0∫1wal(l,t)dt,其中 l = i ⊕ j l=i\oplus j l=i⊕j
根据 ∫ 0 1 w a l ( 0 , t ) d t = 1 \int\limits_0^1 wal(0,t)dt = 1 0∫1wal(0,t)dt=1 ∫ 0 1 w a l ( i , t ) d t = 0 ( i > 0 ) \int\limits_0^1wal(i,t)dt=0 \quad(i>0) 0∫1wal(i,t)dt=0(i>0)
所以当 i = j = 0 i=j=0 i=j=0时,有 ∫ 0 1 w a l ( i , t ) ⋅ w a l ( j , t ) d t = 1 \int\limits_0^1 wal(i,t)\cdot wal(j,t)dt = 1 0∫1wal(i,t)⋅wal(j,t)dt=1
否则 i ≠ j i\neq j i=j,则 ∫ 0 1 w a l ( i , t ) ⋅ w a l ( j , t ) d t = 0 \int\limits_0^1wal(i,t)\cdot wal(j,t)dt=0 0∫1wal(i,t)⋅wal(j,t)dt=0
正交性得证