4. 树（二叉树、二叉查找树/二叉排序树/二叉搜索树、平衡二叉树、平衡二叉B树/红黑树）

本文章里的部分照片来源于网络，特此声明，侵权联系删除！

								二叉树
								  |
								  | （由于二叉树存入的数据是无规则的）
								  |
					二叉查找树（二叉排序树、二叉搜索树）  
								  |
								  |	（由于二叉做查找树的两条子树的高度可能相差太大）
								  |
							  平衡二叉树	
							      |
								  |	（由于平衡二叉树添加数据可能需要旋转，浪费时间）
								  |
					     红黑树（平衡二叉B树）			    

1. 二叉树

1.1 概述

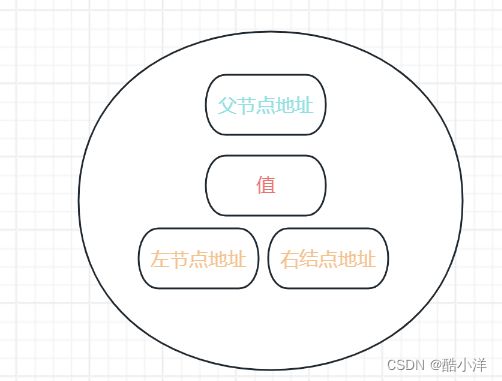
二叉树是一种常见的树状数据结构，由节点组成，每个节点最多有两个子节点，分别称为左子节点和右子节点。

• 二叉树中,任意一个节点的度要小于等于2

• 左子节点的值小于或等于当前节点的值

• 右子节点的值大于当前节点的值。

• 二叉树可以为空树，也可以只有一个根节点。

节点内部结构：

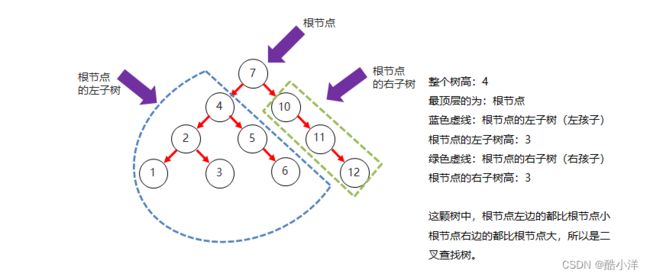
二叉树结构图：

1.2 特点

二叉树是一种常见的树状数据结构，它由节点组成，每个节点最多有两个子节点。

具有以下特点：

1. 根节点：树的顶部节点，没有父节点。

2. 叶子节点：没有子节点的节点。

3. 左子节点和右子节点：一个节点只能有最多两个子节点，其中一个是左子节点，另一个是右子节点。

4. 子树：每个节点都可以作为根节点，形成一颗子树。

5. 深度：树中节点的最大层次数。

6. 高度：树中节点的最大深度。

1.3 二叉树遍历方式

1.3.1 前序遍历(先序遍历)

前序遍历(先序遍历）: 从根节点开始，然后按照当前节点，左子结点，右子节点的顺序遍历

前序遍历是二叉树遍历的一种方式，也被称为先序遍历。

在前序遍历中，先访问根节点，然后按照先左后右的顺序继续遍历左子树和右子树。

前序遍历的步骤：

1. 访问当前节点。

2. 递归地前序遍历左子树。

3. 递归地前序遍历右子树。

举个例子，考虑如下的二叉树：

     A
   /   \
  B     C
 / \   / \
D   E F   G

通过前序遍历，节点的访问顺序将会是：A - B - D - E - C - F - G。具体操作如下：

1. 访问节点 A。
2. 递归前序遍历左子树，访问节点 B。
3. 递归前序遍历左子树，访问节点 D。
4. 左子树为空，返回到节点 B。
5. 递归前序遍历右子树，访问节点 E。
6. 右子树为空，返回到节点 B。
7. 返回到节点 A。
8. 递归前序遍历右子树，访问节点 C。
9. 递归前序遍历左子树，访问节点 F。
10. 左子树为空，返回到节点 C。
11. 递归前序遍历右子树，访问节点 G。
12. 右子树为空，返回到节点 C。

前序遍历的结果是：A - B - D - E - C - F - G。

1.3.2 中序遍历

中序遍历:从最左边的子节点开始，然后按照左子结点，当前节点，右子节点的顺序遍历

中序遍历是二叉树遍历的一种方式。

在中序遍历中，先访问左子树，然后访问根节点，最后访问右子树。

中序遍历的步骤：

1. 递归地中序遍历左子树。

2. 访问当前节点。

3. 递归地中序遍历右子树。

举个例子，考虑如下的二叉树：

     A
   /   \
  B     C
 / \   / \
D   E F   G

通过中序遍历，节点的访问顺序将会是：D - B - E - A - F - C - G。具体操作如下：

1. 递归中序遍历左子树，访问节点 D。
2. 左子树为空，返回到节点 B。
3. 中序遍历访问节点 B。
4. 递归中序遍历左子树，访问节点 E。
5. 左子树为空，返回到节点 B。
6. 返回到节点 A。
7. 递归中序遍历右子树，访问节点 F。
8. 中序遍历访问节点 C。
9. 递归中序遍历左子树，访问节点 G。
10. 左子树为空，返回到节点 C。

中序遍历的结果是：D - B - E - A - F - C - G。

1.3.3 后序遍历

后序遍历:从最左边的子节点开始，然后按照左子结点，右子节点，当前节点的顺序遍历

后序遍历是二叉树遍历的一种方式。

在后序遍历中，先访问左子树，然后访问右子树，最后访问根节点。

后序遍历的步骤：

1. 递归地后序遍历左子树。

2. 递归地后序遍历右子树。

3. 访问当前节点。

举个例子，考虑如下的二叉树：

     A
   /   \
  B     C
 / \   / \
D   E F   G

通过后序遍历，节点的访问顺序将会是：D - E - B - F - G - C - A。具体操作如下：

1. 递归后序遍历左子树，访问节点 D。
2. 左子树为空，返回到节点 B。
3. 递归后序遍历右子树，访问节点 E。
4. 右子树为空，返回到节点 B。
5. 后序遍历访问节点 B。
6. 递归后序遍历左子树，访问节点 F。
7. 左子树为空，返回到节点 C。
8. 递归后序遍历右子树，访问节点 G。
9. 右子树为空，返回到节点 C。
10. 后序遍历访问节点 C。
11. 返回到节点 A。
12. 后序遍历访问节点 A。

后序遍历的结果是：D - E - B - F - G - C - A。

1.3.4 层序遍历

层序遍历:从根节点开始一层一层的遍历。

层序遍历是二叉树遍历的一种方式。

在层序遍历中，按照从上到下、从左到右的顺序逐层访问节点。

层序遍历的步骤：

1. 将根节点入队。

2. 循环执行以下操作直到队列为空：

   • 出队一个节点，访问该节点。

   • 如果该节点有左子节点，则将左子节点入队。

   • 如果该节点有右子节点，则将右子节点入队。

举个例子，考虑如下的二叉树：

     A
   /   \
  B     C
 / \   / \
D   E F   G

通过层序遍历，节点的访问顺序将会是：A - B - C - D - E - F - G。具体操作如下：

1. 将根节点 A 入队。
2. 出队节点 A，并访问节点 A。
3. 将左子节点 B 入队。
4. 将右子节点 C 入队。
5. 出队节点 B，并访问节点 B。
6. 将左子节点 D 入队。
7. 将右子节点 E 入队。
8. 出队节点 C，并访问节点 C。
9. 将左子节点 F 入队。
10. 将右子节点 G 入队。
11. 出队节点 D，并访问节点 D。
12. 出队节点 E，并访问节点 E。
13. 出队节点 F，并访问节点 F。
14. 出队节点 G，并访问节点 G。

层序遍历的结果是：A - B - C - D - E - F - G。

2. 二叉查找树（二叉排序树、二叉搜索树）

2.1 概述

二叉查找树（Binary Search Tree，BST）是一种特殊的二叉树结构，在这种树中，每个节点的值都大于其左子树中的任何节点的值，且小于其右子树中的任何节点的值。这使得二叉查找树具有高效的搜索和插入操作。

• 二叉查找树,又称二叉排序树或者二叉搜索树

2.2 特点

• 二叉查找树的特点

  • 每一个节点上最多有两个子节点

  • 左子树上所有节点的值都小于根节点的值

  • 右子树上所有节点的值都大于根节点的值

  • 没有重复的节点值。

• 二叉查找树结构图

  

• 二叉查找树和二叉树对比结构图

  

• 二叉查找树添加节点规则

  • 小的存左边

  • 大的存右边

  • 一样的不存

  

3. 平衡二叉树

3.1 概述

平衡二叉树（Balanced Binary Tree），也称为 AVL 树（平衡二叉搜索树），是一种特殊的二叉查找树，它的特点是每个节点的左子树和右子树的高度差不超过1。

平衡二叉树的设计目的是为了保持二叉树的平衡性，以提高查找、插入和删除操作的效率。普通的二叉查找树在某些情况下可能会退化为链表，导致操作的时间复杂度从平均情况下的 O(logn) 变成最坏情况下的 O(n)，而平衡二叉树的高度始终保持在 logn 的范围内，保证了操作的高效性。

在平衡二叉树中，每个节点都有一个平衡因子（balance factor），定义为左子树的高度减去右子树的高度。平衡因子可以使平衡二叉树保持平衡。当插入或删除一个节点时，可能会破坏平衡，此时需要通过旋转操作来调整树的结构，使其重新满足平衡性的要求。

3.2 特点

• 平衡二叉树的特点

  • 二叉树左右两个子树的高度差不超过1

  • 任意节点的左右两个子树都是一颗平衡二叉树

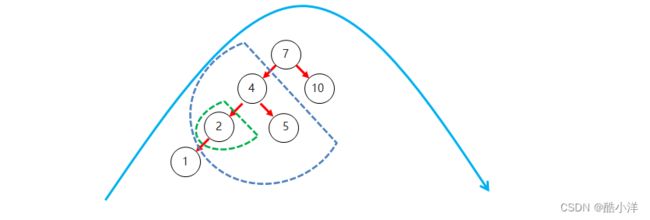
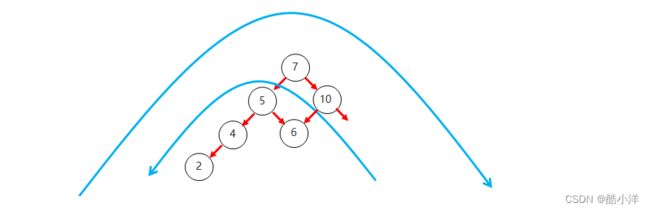
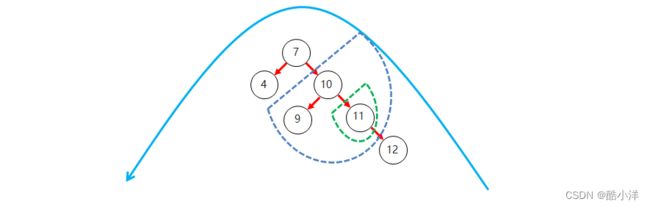
3.3 旋转

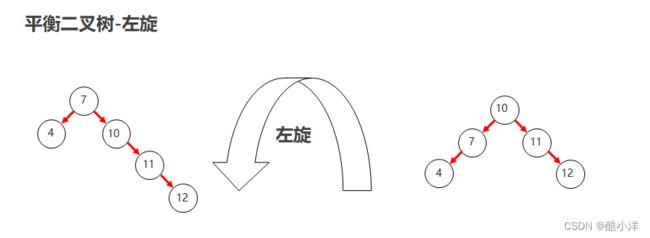
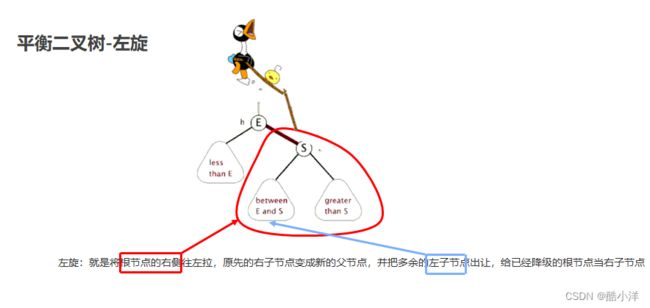
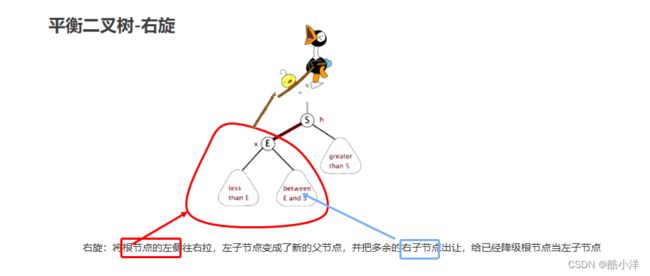
• 旋转触发时机：当添加一个节点之后,该树不再是一颗平衡二叉树

3.3.1 左旋

• 就是将根节点的右侧往左拉,原先的右子节点变成新的父节点,并把多余的左子节点出让,给已经降级的根节点当右子节点

  
  

3.3.2 右旋

• 就是将根节点的左侧往右拉,左子节点变成了新的父节点,并把多余的右子节点出让,给已经降级根节点当左子节点

  
  

3.4 平衡二叉树旋转的四种情况

3.4.1 左左

• 左左: 当根节点左子树的左子树有节点插入,导致二叉树不平衡

  • 如何旋转: 直接对整体进行右旋即可

  

3.4.2 左右

• 左右: 当根节点左子树的右子树有节点插入,导致二叉树不平衡

  • 如何旋转: 先在左子树对应的节点位置进行左旋,在对整体进行右旋

    

3.4.3 右右

• 右右: 当根节点右子树的右子树有节点插入,导致二叉树不平衡

  • 如何旋转: 直接对整体进行左旋即可
    

3.4.4 右左

• 右左:当根节点右子树的左子树有节点插入,导致二叉树不平衡

  • 如何旋转: 先在右子树对应的节点位置进行右旋,在对整体进行左旋

    

• 平衡二叉树和二叉查找树对比结构图
  

4. 红黑树（平衡二叉B树）

4.1 概述

红黑树（Red-Black Tree）是一种自平衡的二叉查找树，它在进行插入和删除等操作时能够自动调整树的结构，以保持树的平衡性。红黑树的设计目的是在维持平衡的同时提供较高的插入、删除和查找效率。

红黑树的名称来源于每个节点上的一个额外的属性，即节点的颜色，可以是红色或黑色。

红黑树的插入和删除操作都会涉及到节点的颜色变化和旋转操作，通过这些操作来保持树的平衡性。相较于其他平衡二叉树如 AVL 树，红黑树的实现相对简单，并且对于插入和删除操作的限制较少，因此在实际应用中更为常见。

节点内部结构：

4.2 特点

• 红黑树的特点

  • 平衡二叉B树

  • 每一个节点可以是红或者黑

  • 红黑树不是高度平衡的,它的平衡是通过"自己的红黑规则"进行实现的

4.3 规则

• 红黑树的红黑规则：

  1. 每一个节点或是红色的,或者是黑色的

  2. 根节点必须是黑色

  3. 如果一个节点没有子节点或者父节点,则该节点相应的指针属性值为Nil,这些Nil视为叶节点,每个叶节点(Nil)是黑色的

  4. 如果某一个节点是红色,那么它的子节点必须是黑色(不能出现两个红色节点相连 的情况)

  5. 对每一个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点

     

• 红黑树添加节点的默认颜色

  • 添加节点时,默认为红色,效率高

    

4.4 添加节点

• 红黑树添加节点后保持红黑规则方法：

  • 根节点位置
    • 直接变为黑色
  • 非根节点位置
    • 父节点为黑色
      • 不需要任何操作,默认红色即可
    • 父节点为红色
      • 叔叔节点为红色

        1. 将"父节点"设为黑色,将"叔叔节点"设为黑色

        2. 将"祖父节点"设为红色

        3. 如果"祖父节点"为根节点,则将根节点再次变成黑色

      • 叔叔节点为黑色

        1. 将"父节点"设为黑色

        2. 将"祖父节点"设为红色

        3. 以"祖父节点"为支点进行旋转