1.25学习总结1
图的遍历
图的遍历
图的基本概念
由一些小圆点(顶点)和连接这些小圆点的线(边)组成的。通常表示为: G (V,E) ,其中,G 表示一个图,V 是图G中顶点的集合,E 是图G中边的集合。通常,我们把点与点之间不带箭头的线叫做边,带箭头的线叫做弧。
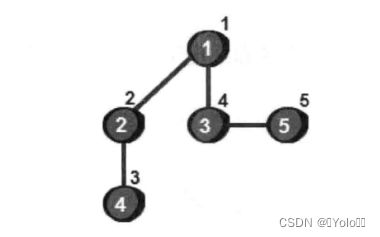
如图,点(1,2,3,4,5)和边(1-2,1-3,1-5,2-4,3-5)组成图
无向图
如果一个图是由点和边所构成的,称为无向图,记作G=(V, E),其中V表示无向图G的点集合,E表示图G的边集合。连接点vi,vj的边记作[vi, vj],或者[vj, vi]。
有向图
如果一个图是由点和弧所构成的,称为有向图,记作D=(V, A),其中V表示有向图D的点集合,A表示有向图D的弧集合。一条方向从vi指向vj的弧,记作(vi, vj)。
连通图
图中任意两点之间均至少有一条通路称为连通图,否则称为不连通图;在无向图中, 若从顶点v1到顶点v2有路径, 则称顶点v1与v2是连通的。如果图中任意一对顶点都是连通的,则称此图是连通图。
遍历
从已给图的某一顶点出发,沿着一些边访遍图中所有的顶点,且使每个顶点仅被访问一次,就叫做图的遍历。
时间戳
每个顶点右上方的数即这个顶点是第几个被访问到的,这个数叫时间戳。
图的邻接矩阵存储法
下列二维数组第i行第j列表示 的即点i到点j是否有边,1代表有边,/代表无边,0代表i=j
这种存储图的方法即图的邻接矩阵存储法
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 2 | 1 |
| 2 | 1 | 0 | 2 | 1 | 2 |
| 3 | 1 | 2 | 0 | 2 | 1 |
| 4 | 2 | 1 | 2 | 0 | 2 |
| 5 | 1 | 2 | 1 | 2 | 0 |
深度优先遍历
主要思想
从图中某一起始顶点V出发,访问它的任一邻接顶点V1,再从V1出发,访问与V1邻接但还未被访问过的顶点V2;然后再从V2出发,重复步骤直至到达所有的邻接顶点都被访问过的顶点Vn为止,接着,退回一步,退到前一次刚访问过的顶点,看是否还有其它没有被访问过的邻接点。如果有,则访问此顶点,之后再从此顶点出发,进行与前述类似的访问;如果没有,就再退回一步进行访问.重复上述过程,直到连通图中所有顶点都被访问过为止。
主要代码
void dfs(int spot)//spot为此时的顶点编号
{
printf("%d ",spot);
sum++;//访问的顶点数加一
if(sum==n) return;//sum=n时所有顶点都已访问,退出
for(i=1;i<=n;i++)
{
if(e[spot][i]==1&&book[i]==0)
//判断spot到i是否有边,且是否被访问过
{
book[i]==1;//标记i被访问过
dsf(i);//继续遍历
}
}
return;
} 完整代码
#include
int n;
int sum;//访问的顶点数
int book[110];//记录那些顶点已经访问过
int c[110][110];//邻接矩阵
void dfs(int spot)//spot为此时的顶点编号
{
int i;
printf("%d ",spot);
sum++;//访问的顶点数加一
if(sum==n) return;//sum==n时所有顶点都已访问,退出
for(i=1;i<=n;i++)
{
if(c[spot][i]==1&&book[i]==0)//判断spot到i是否有边,且是否被访问过
{
book[i]=1;//标记i被访问过
dfs(i);//继续遍历
}
}
return;
}
int main()
{
int i,j,m,a,b;
scanf("%d %d",&n,&m);
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(i==j) c[i][j]=0;
else c[i][j]=2;
for(i=1;i<=m;i++)//输入顶点之间的边
{
scanf("%d %d",&a,&b);
c[a][b]=1;
c[b][a]=1;
}
book[1]=1;//从点1开始
dfs(1);
return 0;
} 
广度优先遍历
主要思想
从图的某一顶点出发,首先依次访问该顶点的所有邻接点,再按这些顶点被访问的先后次序依次访问与他们相邻接的所有未被访问的顶点,重复此过程,直至所有顶点均被访问为止。
图解
主要代码
while(headn)//判断是否所有定点都已被访问过
break;
}
head++;//继续往下扩展
}
完整代码
#include
int main()
{
int i,j,n,m,a,b;
int book[110]={0},c[110][110],spot;
scanf("%d %d",&n,&m);
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(i==j) c[i][j]=0;
else c[i][j]=2;
for(i=1;i<=m;i++)//输入顶点之间的边
{
scanf("%d %d",&a,&b);
c[a][b]=1;
c[b][a]=1;
}
int que[10010],head=1,tail=1;
que[tail]=1;//顶点1出发,将顶点1加入队列
tail++;
book[1]=1;//顶点1已访问
while(headn)//判断是否所有定点都已被访问过
break;
}
head++;
}
for(i=1;i 城市地图
思路
运用深度优先遍历(有向图)
min用于存放最短路程,每得到一个路程值与min比较,小于min则更新min的值:
void dsf(int spot,int sum)//spot表示城市编号,sum表示目前走过的路程
{
int i;
if(sum>min) return;//如果目前走过的路程大于之前找到的最短路程,返回
if(spot==n)//是否到达目的地
{
if(sum如果未到达目的地,则对下一点进行判断,即此点到下一点是否有路,是否已在路径中,用book[i]判断是否已在路径中,如果这个点符合要求,则对这个点进行下一步扩展:
for(i=1;i<=n;i++)
{
if(L[spot][i]!=999999999&&book[i]==0)//判断spot到i是否有路,且是否已在路径中
{
book[i]=1;//标记i已在路径中
dsf(i,sum+L[spot][i]);//从i出发,继续寻找
book[i]=0;//取消标记
}
}完整代码
#include
int min=999999999,book[110],n,L[110][110];
void dsf(int spot,int sum)//spot表示城市编号,sum表示目前走过的路程
{
int i;
if(sum>min) return;//如果目前走过的路程大于之前找到的最短路程,返回
if(spot==n)//是否到达目的地
{
if(sum 最少转机
找到一种转机方式,使转机次数最少
思路
运用广度优先遍历(无向图)
完整代码
#include
struct note
{
int x;//城市编号
int s;//转机次数
};
int main()
{
struct note que[2510];
int i,j,n,m,a,b,spot,start,end,flag=0;
int book[51]={0},c[51][51]={0};
scanf("%d %d %d %d",&n,&m,&start,&end);
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(i==j) c[i][j]=0;
else c[i][j]=99999999;
for(i=1;i<=m;i++)
{
scanf("%d %d",&a,&b);
c[a][b]=1;
c[b][a]=1;
}
int head=1,tail=1;
que[tail].x=start;//从start出发,将start入队
que[tail].s=0;
tail++;
book[start]=1;//标记start已在队列中
while(head