Leetcode第383场周赛

Leetcode第383场周赛

本人水平有限，只做前3道。

一、边界上的蚂蚁

边界上有一只蚂蚁，它有时向 左 走，有时向 右 走。

给你一个 非零 整数数组 nums 。蚂蚁会按顺序读取 nums 中的元素，从第一个元素开始直到结束。每一步，蚂蚁会根据当前元素的值移动：

如果 nums[i] < 0 ，向 左 移动 -nums[i]单位。
如果 nums[i] > 0 ，向 右 移动 nums[i]单位。
返回蚂蚁 返回 到边界上的次数。

注意：

边界两侧有无限的空间。
只有在蚂蚁移动了 |nums[i]| 单位后才检查它是否位于边界上。换句话说，如果蚂蚁只是在移动过程中穿过了边界，则不会计算在内。

解题思路

找到数组累加和=0的次数

代码

class Solution {
    public int returnToBoundaryCount(int[] nums) {
        int rec = 0,cnt = 0;
        for(int num:nums){
            rec += num;
            if(rec==0){
                cnt++;
            }
        }
        return cnt;
    }
}

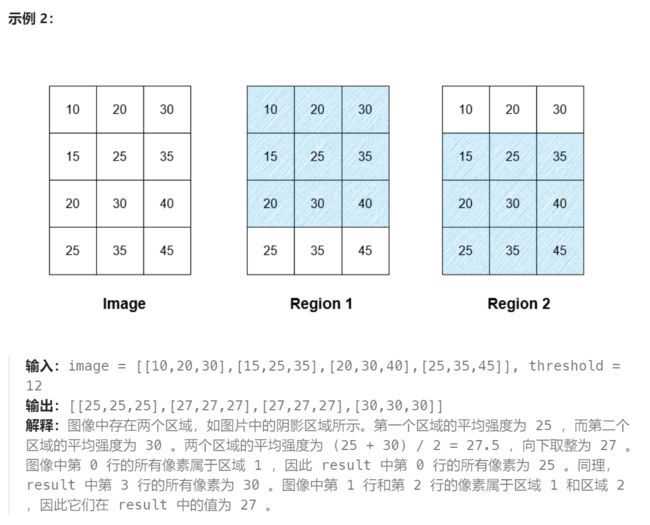
二、找出网格的区域平均强度

给你一个下标从 0 开始、大小为 m x n 的网格 image ，表示一个灰度图像，其中 image[i][j] 表示在范围 [0…255] 内的某个像素强度。另给你一个 非负 整数 threshold 。

如果 image[a][b] 和 image[c][d] 满足 |a - c| + |b - d| == 1 ，则称这两个像素是 相邻像素 。

区域 是一个 3 x 3 的子网格，且满足区域中任意两个 相邻 像素之间，像素强度的 绝对差 小于或等于 threshold 。

区域 内的所有像素都认为属于该区域，而一个像素 可以 属于 多个 区域。

你需要计算一个下标从 0 开始、大小为 m x n 的网格 result ，其中 result[i][j] 是 image[i][j] 所属区域的 平均 强度，向下取整 到最接近的整数。如果 image[i][j] 属于多个区域，result[i][j] 是这些区域的 “取整后的平均强度” 的 平均值，也 向下取整 到最接近的整数。如果 image[i][j] 不属于任何区域，则 result[i][j] 等于 image[i][j] 。

返回网格 result 。

解题思路

这道题考阅读理解。

1. 相邻像素：如果两个像素在网格中水平或垂直相邻（即它们的位置之差的和为1），它们被认为是相邻像素。
2. 区域定义：一个区域是一个 3x3 的子网格，其中任意两个相邻像素的强度之差的绝对值都不超过给定的阈值（threshold）。这意味着，在一个区域内，所有相邻像素的强度都相似。
3. 区域的平均强度：计算一个区域内所有像素强度的平均值。如果一个像素属于多个区域，则需要计算这些区域的平均强度的平均值。在这个计算过程中，所有的平均值都需要向下取整到最接近的整数。
4. result网格：对于image中的每个像素，result中的对应像素应该是该像素所属区域的平均强度。如果一个像素属于多个区域，则取这些区域的平均强度的平均值（都进行向下取整）。如果一个像素不属于任何区域，则result中的对应像素的值等于image中的原始像素值。
   从本质上讲，这个任务是在对图像进行一种特定的平滑处理，其中“平滑”的程度由阈值threshold控制，只有当一个区域内的像素强度变化在threshold定义的范围内时，这些像素的强度才会被平均。

解题思路如下：

1. 遍历所有3x3的子网格。
2. 遍历网格中所有相邻像素(即左右相邻或上下相邻)，如果存在差值大于threshold的情况，则遍历下一个子网格。
3. 如果合法，计算子网格中的平均值avg，等于子网格中的像素值和/9。
4. 更新子网格内的result[i][j]，我们先将avg加到result[i][j]中，同时，我们还需要一个矩阵cnt[i][j]记录image[i][j]在几个子网格中。
5. 如果cnt[i][j]=0，那么result[i][j]=avg。否则，result[i][j]=result[i][j]/cnt[i][j](每次result[i][j]+avg,cnt[i][j]+1)。

代码

class Solution {
    public int[][] resultGrid(int[][] image, int threshold) {
        int m = image.length;
        int n = image[0].length;
        int[][] result = new int[m][n];// 结果数组
        int[][] cnt = new int[m][n];// 存储image[i][j]在子网格中出现的次数
        for (int i = 2; i < m; i++) {
            next:
            for (int j = 2; j < n; j++) {
                // 检查左右相邻格子
                for (int x = i-2; x <= i; x++) {
                    if(Math.abs(image[x][j-2] - image[x][j-1]) > threshold || Math.abs(image[x][j-1] - image[x][j]) > threshold){
                        continue next;   
                    }
                }

                // 检查上下相邻格子
                for (int y = j-2; y <= j; y++) {
                    if(Math.abs(image[i-2][y] - image[i-1][y]) > threshold || Math.abs(image[i-1][y] - image[i][y]) > threshold){
                        continue next;
                    }
                }

                // 合法，计算3x3子网格的平均值
                int avg = 0;
                for (int x = i-2; x <= i; x++) {
                    for (int y = j-2; y <= j; y++) {
                        avg += image[x][y];
                    }
                }

                avg /= 9;

                // 更新3x3子网格内的result
                for (int x = i-2; x <= i; x++) {
                    for (int y = j-2; y <= j; y++) {
                        result[x][y] += avg;
                        cnt[x][y] ++;
                    }
                }
            }
        }

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if(cnt[i][j] == 0){
                    result[i][j] = image[i][j];
                }else{
                    result[i][j] /= cnt[i][j];
                }
            }
        }

        return result;
    }
}

三、将单词恢复初始状态所需的最短时间I

给你一个下标从 0 开始的字符串 word 和一个整数 k 。

在每一秒，你必须执行以下操作：

移除 word 的前 k 个字符。
在 word 的末尾添加 k 个任意字符。
注意 添加的字符不必和移除的字符相同。但是，必须在每一秒钟都执行 两种 操作。

返回将 word 恢复到其 初始 状态所需的 最短 时间（该时间必须大于零）。

示例 1：

输入：word = “abacaba”, k = 3
输出：2
解释：
第 1 秒，移除 word 的前缀 “aba”，并在末尾添加 “bac” 。因此，word 变为 “cababac”。
第 2 秒，移除 word 的前缀 “cab”，并在末尾添加 “aba” 。因此，word 变为 “abacaba” 并恢复到始状态。
可以证明，2 秒是 word 恢复到其初始状态所需的最短时间。
示例 2：

输入：word = “abacaba”, k = 4
输出：1
解释：
第 1 秒，移除 word 的前缀 “abac”，并在末尾添加 “caba” 。因此，word 变为 “abacaba” 并恢复到初始状态。
可以证明，1 秒是 word 恢复到其初始状态所需的最短时间。
示例 3：

输入：word = “abcbabcd”, k = 2
输出：4
解释：
每一秒，我们都移除 word 的前 2 个字符，并在 word 末尾添加相同的字符。
4 秒后，word 变为 “abcbabcd” 并恢复到初始状态。
可以证明，4 秒是 word 恢复到其初始状态所需的最短时间。

解题思路

在每次循环中，从 k 的位置开始提取字符串，直到字符串的末尾存储到cWord中，cWord表示原始word去除前k个字符后的结果。
然后，检查cWord是否可以做原始word的前缀。(即cWord与原始word中长度相等的前缀相同)
如果在任何时刻，cWord可以做原始word前缀，这意味着你可以通过在下一次操作中添加相应的字符来恢复 word 到其初始状态。因此，增加time计数器并退出循环。如果cWord不可以做原始word前缀，则增加time计数器并继续循环，如果同时发现cWord的长度小于k，则说明下一次操作后必定可以使word恢复到原始状态(因为等同于所有字符都进行替换，所以必定有一种可能使其恢复到原始状态)，则增加time计数器并继续循环。

代码

class Solution {
    public int minimumTimeToInitialState(String word, int k) {
        int time = 0;
        String cWord = word;
        while (true) {
            cWord = cWord.substring(k);
            if(word.substring(0,cWord.length()).equals(cWord)){
                time++;
                break;
            }else{
                time++;
                if(cWord.length()<k){
                    time++;
                    break;
                }
            }
        }
        return time;
    }
}