Hello ”树“先生

恭喜发现宝藏！微信搜索公众号【TechGuide】关注更多新鲜好文和互联网大厂的笔经面经。
作者@TechGuide【全网同名】
点赞再看，养成习惯，您动动手指对原创作者意义非凡

当你的才华还撑不起你的野心时，你应该静下心去学习 。

---

20200929
文章末尾已更新最小生成树、线段树等内容

---

前言

首先思考这样一个问题：为什么有树？因为树的光合作用可以吸，呸 ，因为分层次管理（增删改查）数据（在很多场景下）有着更高的效率！

值得注意的是，无论是顺序表、链表、队列还是现在的各种纷繁复杂的树形数据结构，每一个数据结构的提出都是因为解决了其他数据结构解决不了或者效果不够好的问题。

正文

1. 二叉树

关于二叉树基本概念的介绍这里就不再赘述，以下我们重点介绍两个概念，即：

• 二叉搜索树
• 平衡二叉树

2. 二叉搜索树

二叉搜索树中，当前根节点的左边全部比根节点小，当前根节点的右边全部比根节点大。这样的排布无疑对数据的查找是有帮助的，从根节点出发，与节点键值比较递归的与左/右子树根节点比较，最后相等即可判定找到。

但是二叉树在动态查找过程中会有一个问题，由于树的查找效率与树的高度直接相关，如果多次的增删节点使得二叉搜索树变得”瘦高“，其效果会退化成一个链表结构，而且，在不同的节点插入顺序的情况下，会形成不同深度的树形结构（如上图），经过分析ASL（平均查找长度），我们可以知道中间最”平衡”的二叉树效率最高。所以综上，我们就可以引出我平衡二叉树来解决这个问题了。

平衡二叉树（AVL树）任意节点的左右子树高度差的绝对值不超过1。高度h = $O(lg(N))$。

很多小伙伴不知道AVL代表什么，实际是发明这种数据结构的科学家们的首字母构成的。

怎么解决二叉搜索树碰到的不平衡的问题呢？既然你歪了一点，那自然第一个想到的就是再调整。如何调整呢？可以通过右旋，或者左旋来调整树形结构。

RR旋转：

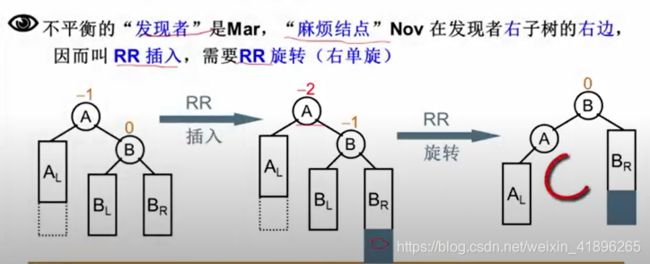
LL旋转：

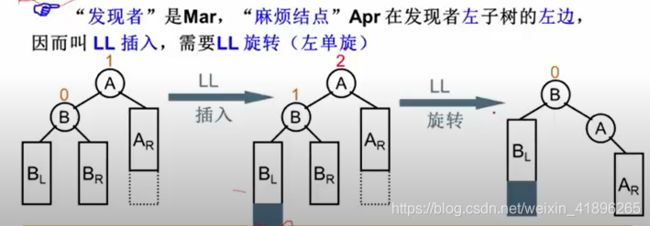
LR旋转：

RL旋转：

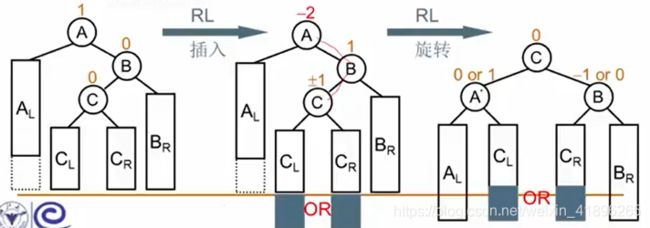
判断方法是根据谁破坏了谁的平衡（即时一个节点的高度差（平衡因子）大于1了），就做相应的旋转即可。

这里插播一条关于堆的介绍。可以用树来实现堆（优先队列）。
用二叉搜索树？NOOOO！如果一直删最大值，二叉搜索树又退化成链表了。但是是不是就没戏了呢？也不是，做一些调整又可以避免这个缺点了，那就是把最大/小值存在一棵完全二叉树的根节点位置，这样就算删去也不会影响平衡因子了。但是，这样操作之后剩下的部分如何调整成一个正常的树形结构呢？
好，以上是我们关于堆的一些小思考，事实上，堆可以用数组表示的完全二叉树构成，并且其任意节点是其子树所有节点的最大值/最小值。

哈夫曼树

引出哈夫曼树要解决的问题就是如何根据节点不同的查找频率构造更加有效的搜索树？

比如下列示例，根据学生成绩分布构造一棵搜索树：

先给出一个概念： 带权路径长度。这里的全职可以理解为查询频率。

构造哈夫曼树的方法也很简单，就是每次把权值最小的两颗二叉树合并即可。比如：

那么先1，2得到3，再3，3得到6，再4，5得到9，再6，9得到15即可。得到的哈夫曼树如下图：

3. B树

既然有了AVL树了，AVL树的查找又稳定，查找、插入、删除的时间复杂度都为$O（logN）$，不是挺好的吗？为什么还需要B树呢？

1. 这是因为B树由于要维持自身的平衡，所以进行插入和删除结点操作的时候，需要对结点进行频繁的旋转。
2. 同时，AVL树每一个节点只能存放一个元素，并且每个节点只有两个子节点。当进行查找时，就需要多次磁盘IO，（数据是存放在磁盘中的，每次查询是将磁盘中的一页数据加入内存，树的每一层节点存放在一页中，不同层数据存放在不同页。）这样如果需要多层查询就需要多次磁盘IO。

为了解决AVL树上述的问题，就出现了B树。

B树也是一种平衡查找树，只不过是一种多路的平衡查找树。它的结构规则是这样的：

（1）排序方式：所有节点关键字是按递增次序排列，并遵循左小右大原则；

（2）子节点数：非叶节点的子节点数>1，且<=M ，且M>=2，空树除外（注：M阶代表一个树节点最多有多少个查找路径，M=M路,当M=2则是2叉树,M=3则是3叉）；

（3）关键字数：枝节点的关键字数量大于等于ceil(m/2)-1个且小于等于M-1个；

（4）所有叶子节点均在同一层、叶子节点除了包含了关键字和关键字记录的指针外也有指向其子节点的指针只不过其指针地址都为null对应下图最后一层节点的空格子;

关于B树的查询和插入、删除等操作，这里有一篇非常形象的文章，看一遍操作就理解透彻了【传送门】

看完了吗？回来，我总结一下：

1. 查询时，就是通过与节点比较，再按照节点划分值域得到指向下一个节点的指针，再去比较，直到找到，或者到null。
2. 插入时，就是一个节点内的关键字数达到拆分条件时，取出中间值作为父节点，再次添加新节点。
3. 删除节点时，关键字数小于一定值就需要合并关键值。
   
   

说明：
B树相对于平衡二叉树的不同是，每个节点包含的关键字增多了，特别是在B树应用到数据库中的时候，数据库充分利用了磁盘块的原理（磁盘数据存储是采用块的形式存储的，每个块的大小为4K，每次IO进行数据读取时，同一个磁盘块的数据可以一次性读取出来）把节点大小限制和充分使用在磁盘快大小范围；把树的节点关键字增多后树的层级比原来的二叉树少了，减少了数据查找的次数和复杂度;


缺点：
Buuuut,B树也有它的问题，那就是，B树的查找不稳定，最好的情况就是在根节点查到了，最坏的情况就是在叶子结点查到。另外，B树在遍历方面比较麻烦，由于需要进行中序遍历，所以也会进行一定数量的磁盘IO。
为了解决这些问题，出现了B+树。

4. B+树

规则（引自这里）：

（1）B+跟B树不同B+树的非叶子节点不保存关键字记录的指针，只进行数据索引，这样使得B+树每个非叶子节点所能保存的关键字大大增加；

（2）B+树叶子节点保存了父节点的所有关键字记录的指针，所有数据地址必须要到叶子节点才能获取到。所以每次数据查询的次数都一样；

（3）B+树叶子节点的关键字从小到大有序排列，左边结尾数据都会保存右边节点开始数据的指针。

特点：

1、B+树的层级更少：相较于B树B+每个非叶子节点存储的关键字数更多，树的层级更少所以查询数据更快；

2、B+树查询速度更稳定：B+所有关键字数据地址都存在叶子节点上，所以每次查找的次数都相同所以查询速度要比B树更稳定;

3、B+树天然具备排序功能：B+树所有的叶子节点数据构成了一个有序链表，在查询大小区间的数据时候更方便，数据紧密性很高，缓存的命中率也会比B树高。

4、B+树全节点遍历更快：B+树遍历整棵树只需要遍历所有的叶子节点即可，，而不需要像B树一样需要对每一层进行遍历，这有利于数据库做全表扫描。

B树相对于B+树的优点是，如果经常访问的数据离根节点很近，而B树的非叶子节点本身存有关键字其数据的地址，所以这种数据检索的时候会比B+树更快。

5. 红黑树

红黑树也叫RB树，RB-Tree。是一种自平衡的二叉查找树，它的节点的颜色为红色和黑色。它不严格控制左、右子树高度或节点数之差小于等于1。也是一种解决二叉查找树极端情况的数据结构。

红黑树规定了：

1.节点是红色或黑色。

2.根节点是黑色。

3.每个叶子节点都是黑色的空节点（NIL节点）。

4 每个红色节点的两个子节点都是黑色。也就是说从每个叶子到根的所有路径上不能有两个连续的红色节点)。

5.从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

这里有关于红黑树具体操作的详细演示，比较繁杂，但是总结起来就是：

红黑树在查找方面和AVL树操作几乎相同。但是在插入和删除操作上，AVL树每次插入删除会进行大量的平衡度计算，红黑树是牺牲了严格的高度平衡的优越条件为代价，它只要求部分地达到平衡要求，结合变色，降低了对旋转的要求，从而提高了性能。红黑树能够以O(log2 n)的时间复杂度进行搜索、插入、删除操作。此外，由于它的设计，任何不平衡都会在三次旋转之内解决。

相比于BST，因为红黑树可以能确保树的最长路径不大于两倍的最短路径的长度，所以可以看出它的查找效果是有最低保证的。在最坏的情况下也可以保证O(logN)的，这是要好于二叉查找树的。因为二叉查找树最坏情况可以让查找达到O(N)。

总结

1、从平衡二叉树、B树、B+树、B*树总体来看它们的贯彻的思想是相同的，都是采用二分法和数据平衡策略来提升查找数据的速度；

2. 不同点是他们一个一个在演变的过程中通过IO从磁盘读取数据的原理进行一步步的演变，每一次演变都是为了让节点的空间更合理的运用起来，从而使树的层级减少达到快速查找数据的目的；

以上截图来自于北理工ACM培训课