MATLAB GUI 之 插补(逐点比较法、数字积分法DDA的直线圆弧插补)
本科实验周做的东西,效果不错,特此分享。
因代码内容过长,仅开源部分简单内容,更多请转至资源下载。资源中的文件可以直接编译运行。
资源包链接:后续整理上传,需要的同学可先收藏关注或留言。
MATLABGUI之插补//逐点比较法、数字积分发DDA的直线、圆弧插补源代码资源包)-VB文档类资源-CSDN文库
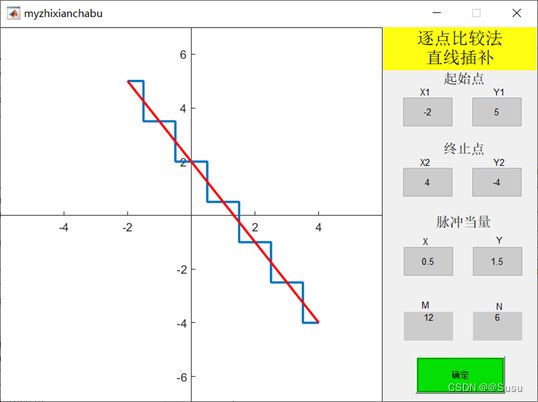
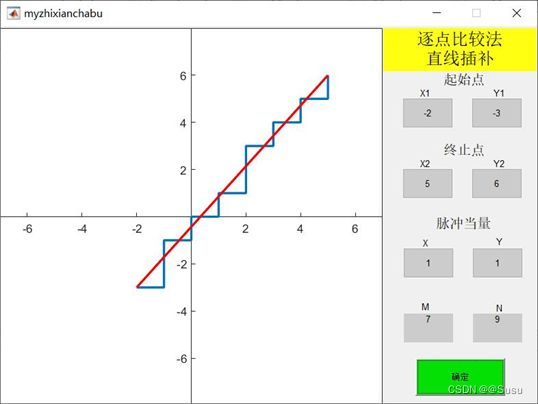
一、逐点比较法直线插补
基本原理:
在刀具按要求轨迹运动加工零件轮廓的过程中,不断比较刀具与被加工零件轮廓之间的相对位置,并根据比较结果决定下一步的进给方向,使刀具向减小偏差的方向进给(始终只有一个方向)。
一般地,逐点比较法插补过程有四个处理节拍,如图所示:
![]()
实现效果:全象限、任意脉冲当量的插补,且会自动得出分别向X轴、Y轴方向的进给总次数,效果如图:
实现代码:(此处代码仅为GUI里调用的插补函数部分,也即“chabu()”,参考网上已有代码修改,GUI部分过长,一并放入资源中供下载)
function [res_x,res_y] = chabu(start_x,start_y,current_x,current_y,end_x,end_y,step_x,step_y)
%
% Take step_x and step_y as the step values in the horizontal and vertical directions,
% then use the point by point comparison method to return the linear interpolation
% from point (start_x, start_y) to point (end_x, end_y)
%
% 以step_x,step_y为横纵方向步进值,逐点比较法返回从点(start_x,start_y)到点(end_x,end_y)的直线插值
%
% 输入参数(start_x, start_y):开始点横纵坐标
% 输入参数(end_x, end_y):结束点横纵坐标
% 输入参数(current_x,current_y):刀具或绘笔图目前所在的位置
% 输出参数step_x,step_y:刀具或绘笔图的步进值
% 输出参数(res_x,res_y):刀具或绘笔图的轨迹
%
% 常用调用方式:
% [res_x,res_y] = PBPC_Linear_Interpolation(start_x,start_y,current_x,current_y,end_x,end_y,step_x,step_y)
if start_x == end_x
res_x = [];
res_y = [];
res_x(1) = start_x;
res_y(1) = start_y;
counter = 2;
if end_y >= start_y
while(1)
if current_x >= end_x-step_x/2 && current_x <= end_x+step_x/2 && ...
current_y >= end_y-step_y/2 && current_y <= end_y+step_y/2
break
end
current_y = current_y+step_y;
res_x(1,counter) = current_x;
res_y(1,counter) = current_y;
counter = counter+1;
end
else
while(1)
if current_x >= end_x-step_x/2 && current_x <= end_x+step_x/2 && ...
current_y >= end_y-step_y/2 && current_y <= end_y+step_y/2
break
end
current_y = current_y-step_y;
res_x(1,counter) = current_x;
res_y(1,counter) = current_y;
counter = counter+1;
end
end
end
if start_y == end_y
res_x = [];
res_y = [];
res_x(1) = start_x;
res_y(1) = start_y;
counter = 2;
if end_x >= start_x
while(1)
if current_x >= end_x-step_x/2 && current_x <= end_x+step_x/2 && ...
current_y >= end_y-step_y/2 && current_y <= end_y+step_y/2
break
end
current_x = current_x+step_x;
res_x(1,counter) = current_x;
res_y(1,counter) = current_y;
counter = counter+1;
end
else
while(1)
if current_x >= end_x-step_x/2 && current_x <= end_x+step_x/2 && ...
current_y >= end_y-step_y/2 && current_y <= end_y+step_y/2
break
end
current_x = current_x-step_x;
res_x(1,counter) = current_x;
res_y(1,counter) = current_y;
counter = counter+1;
end
end
end
if start_x ~= end_x
k = (start_y-end_y)/(start_x-end_x);
x0 = start_x;
y0 = start_y;
syms x
func = matlabFunction(k*(x-x0)+y0);
res_x = [];
res_y = [];
res_x(1) = start_x;
res_y(1) = start_y;
counter = 2;
if end_x > start_x && end_y >= start_y
while(1)
if current_x >= end_x-step_x/2 && current_x <= end_x+step_x/2 && ...
current_y >= end_y-step_y/2 && current_y <= end_y+step_y/2
break
end
if current_y >= func(current_x)
current_x = current_x+step_x;
res_x(1,counter) = current_x;
res_y(1,counter) = current_y;
counter = counter+1;
else
current_y = current_y+step_y;
res_x(1,counter) = current_x;
res_y(1,counter) = current_y;
counter = counter+1;
end
end
elseif end_x < start_x && end_y >= start_y
while(1)
if current_x >= end_x-step_x/2 && current_x <= end_x+step_x/2 && ...
current_y >= end_y-step_y/2 && current_y <= end_y+step_y/2
break
end
if current_y >= func(current_x)
current_x = current_x-step_x;
res_x(1,counter) = current_x;
res_y(1,counter) = current_y;
counter = counter+1;
else
current_y = current_y+step_y;
res_x(1,counter) = current_x;
res_y(1,counter) = current_y;
counter = counter+1;
end
end
elseif end_x > start_x && end_y < start_y
while(1)
if current_x >= end_x-step_x/2 && current_x <= end_x+step_x/2 && ...
current_y >= end_y-step_y/2 && current_y <= end_y+step_y/2
break
end
if current_y <= func(current_x)
current_x = current_x+step_x;
res_x(1,counter) = current_x;
res_y(1,counter) = current_y;
counter = counter+1;
else
current_y = current_y-step_y;
res_x(1,counter) = current_x;
res_y(1,counter) = current_y;
counter = counter+1;
end
end
elseif end_x < start_x && end_y < start_y
while(1)
if current_x >= end_x-step_x/2 && current_x <= end_x+step_x/2 && ...
current_y >= end_y-step_y/2 && current_y <= end_y+step_y/2
break
end
if current_y <= func(current_x)
current_x = current_x-step_x;
res_x(1,counter) = current_x;
res_y(1,counter) = current_y;
counter = counter+1;
else
current_y = current_y-step_y;
res_x(1,counter) = current_x;
res_y(1,counter) = current_y;
counter = counter+1;
end
end
end
end
end
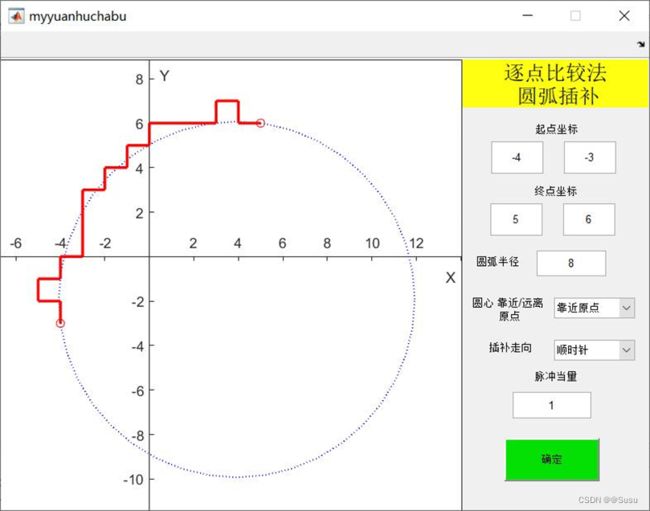
二、逐点比较法圆弧插补
基本原理同逐点比较法直线插补。
实现效果:全象限、任意脉冲当量、顺逆时针走向的圆弧插补。如图:
后续实现代码均放入资源,自行下载。
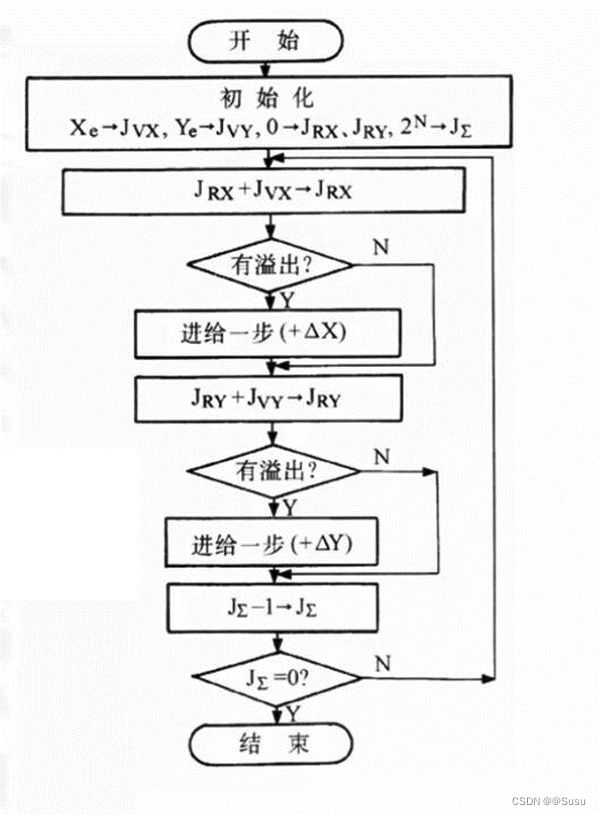
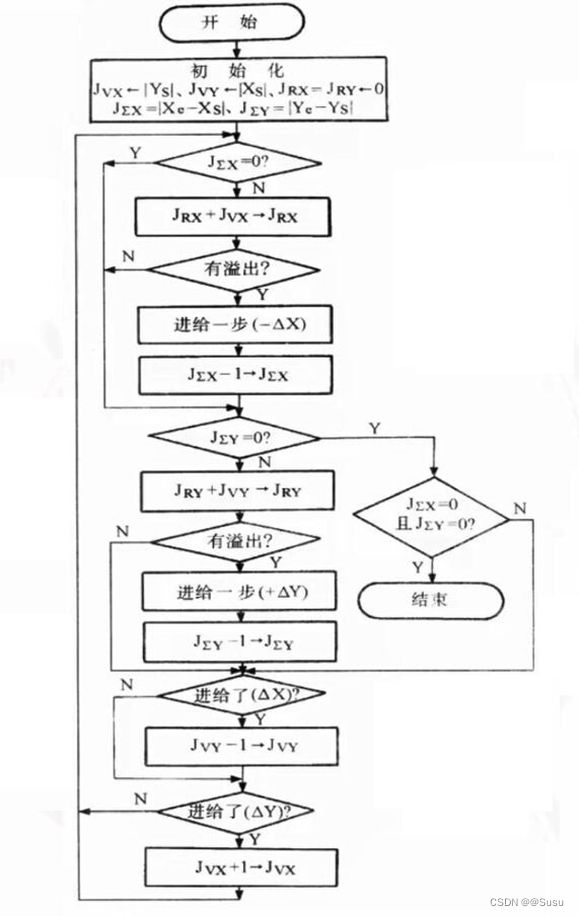
三、数字积分法(DDA)直线、圆弧插补
基本原理:数字积分法插补器的关键部件是累加器和被积函数寄存器,每一个坐标方向就需要一个累加器和一个被积函数寄存器。一般情况下,插补开始前,累加器清零,被积函数寄存器分别寄存Xe和Ye;插补开始后,每来一个累加脉冲▲t,被积函数寄存器里的内容在相应的 累加器中相加一次,相加后的溢出 作为驱动相应坐标轴的进给脉冲▲x (或▲y),而余数仍寄存在累加器 中,当脉冲源发出的累加脉冲数m恰好等于被积函数寄存器的容量2n时,溢出的脉冲数等于以脉冲当量为最小单位的终点坐标,刀具运行到终点。如图所示(前为直线,后为圆弧):
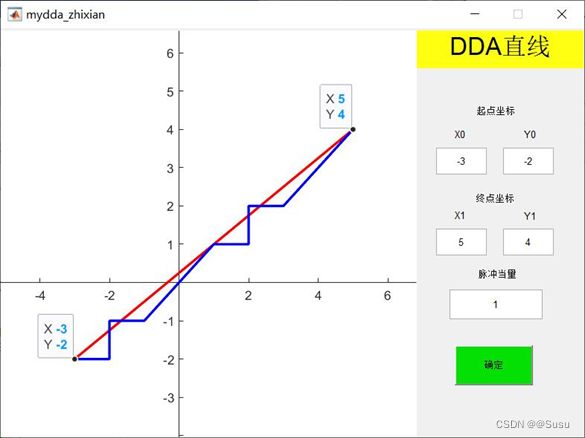
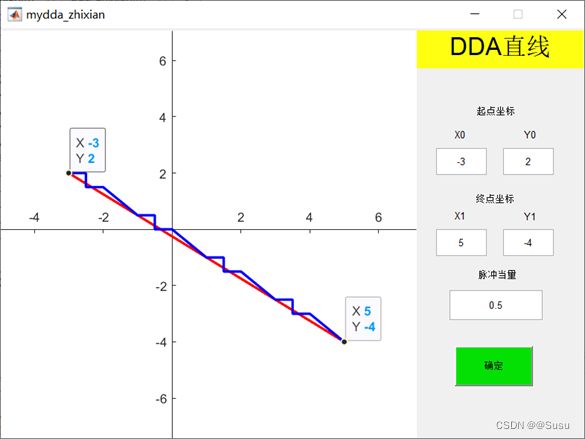
实现效果:DDA直线插补实现了全象限、任意脉冲当量的插补。
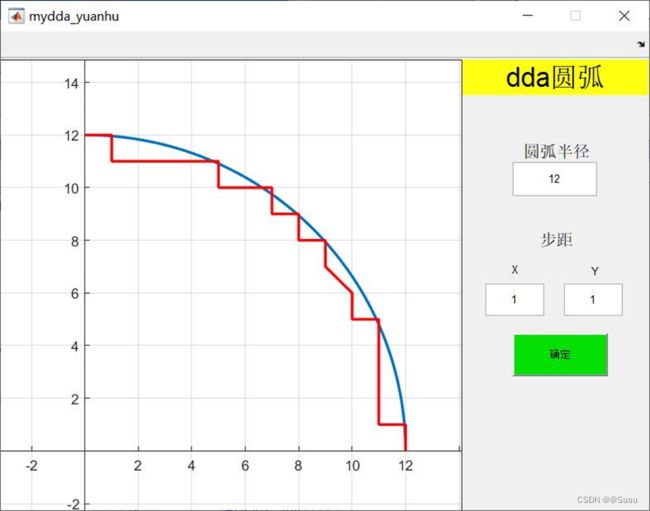
DDA圆弧插补实现了第一象限内任意半径的圆弧插补。
(由于当时时间紧凑,DDA圆弧实现的功能较少,欢迎各方大佬补充)
所参考的资料:老师布置任务时发的一些源文件、百度搜索 Matlab圆弧插补程序+郑国安、数控工作室 最大的中文数控技术学习网站 (busnc.com)、还有一些繁杂而有些小用的CSDN文章,可自行搜索。
本文完。
(据说当时我带领的小组实验周分数最高,并不是我们学校多拉风,毕竟只有5天时间,除了这个还有其他两项任务,之间还要花一天布置任务和答辩,所以有不足的地方还请大佬们多多担待)
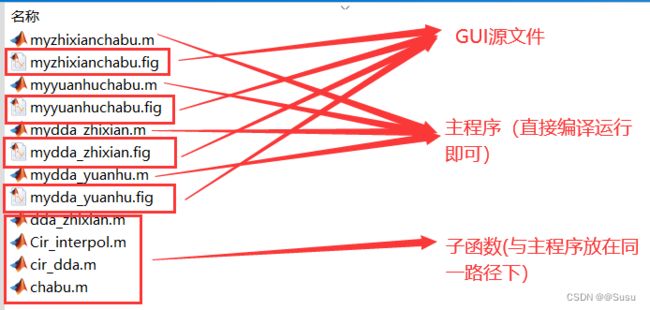
另附资源包文件目录: