机器学习-集成学习（模型融合）方法概述
概述
模型融合方法广泛应用于机器学习中，其原因在于，将多个学习器进行融合预测，能够取得比单个学习器更好的效果，实现“三个臭皮匠，顶一个诸葛亮”，其原因在于通过模型融合，能够降低预测的偏差和方差。本文对模型融合中常见的三种方法进行一个简要介绍：包括Bagging、Boosting、Stacking。
偏差（Bias）与方差（Variance）
假设对数据集中一个样本进行n次预测，偏差是预测期望值与样本值的差异，方差是预测值与预测期望值之间的差异，即偏差反映的是偏离度，方差反映的是稳定性。即：
但是，在实际模型预测中，对于一个样本X，只要模型确定了，无论预测多少次，只会输出一个y值，偏差和方差如何理解呢？可以这么理解：
假设有一群数值约等于y的样本y1, y2, ...yn，对n个样本进行预测可以近似看作对y做了n次预测，预测期望
就是偏差，
就是方差。
降低模型预测偏差与方差的集成方法
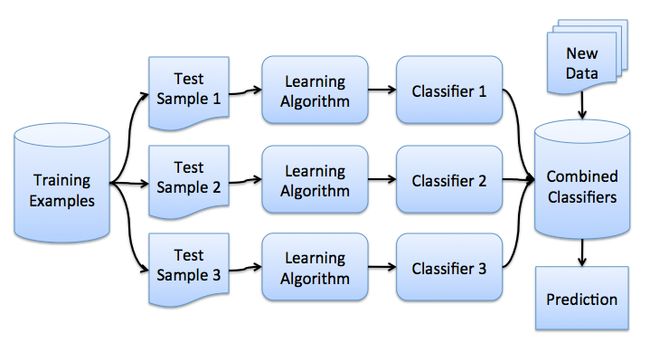
Bagging-Bootstrap Aggregating：降低方差
从字面上理解，Bagging就是放回抽样聚合方法，具体做法是：
1. 采用放回抽样方法训练同时训练多个基学习器（base learner），这多个基学习器是同类型的模型，比如决策树模型。
2. 根据多个基学习器的预测结果取平均值（回归问题）或者选择最多投票类别（分类问题）作为最终的输出结果，通过这种方法可以降低模型预测的方差。
代表算法：随机森林（Random Forest）机器学习-集成学习：随机森林（Random Forest）_毛飞龙的博客-CSDN博客_随机森林拟合
放回抽样方方法（Bootstrap）
假设有m个样本，每次从中随机抽取一个样本，一共抽取m次，因为是放回抽样，因此有些样本会抽取到多次，有些样本未被抽中，未抽中的样本可以作为验证集，如果n足够大，则被抽样出的不同的样本个数占比约为1-1/e = 63%。
效果验证
Bagging对于不稳定的模型效果非常好，比如决策树，能够降低预测误差，但对于稳定性非常好的模型，如线性回归，则基本上没有效果。
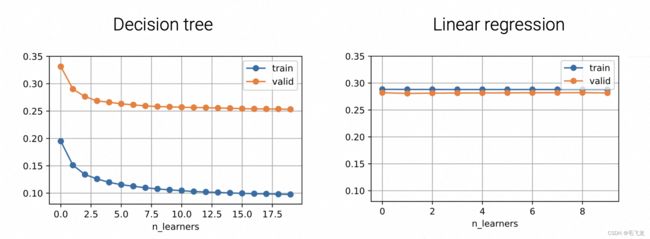图片来源：斯坦福大学2021秋季《实用机器学习课程》
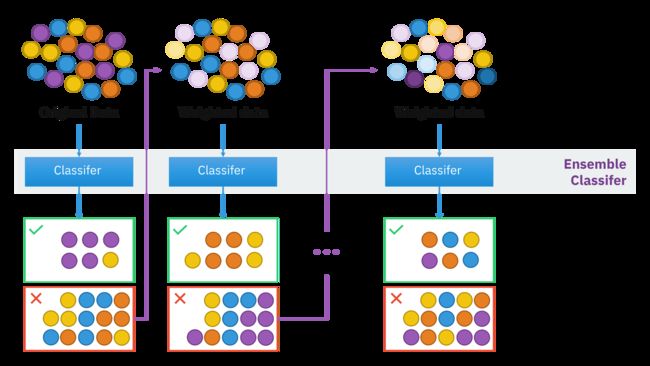
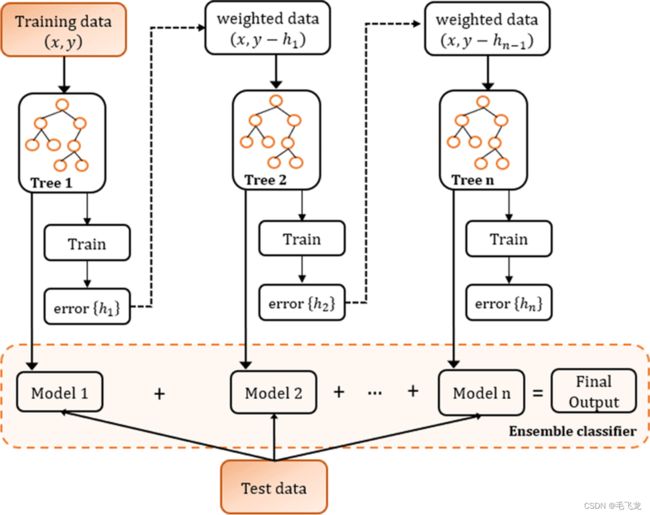
Boosting (降低偏差)
提升树（Boosting Tree）是以分类树或者回归树位基本分类器到提升方法，提升树被认为是统计学习中性能最好的方法之一。
具体做法是：
1. 将基预测器层层叠加、串行的方式训练预测器，每一层在训练的时候，对前一层基预测器分错的样本，给予更高的权重（Ada Boosting），或者让新的预测器对前一个预测器到残差进行拟合（GBDT：机器学习-集成学习-梯度提升决策树（GBDT）_毛飞龙的博客-CSDN博客_gbt决策树）
2. 预测时，根据各层分类器的结果的加权得到最终结果。
Ada Boosting架构
GBDT Boosting算法架构
效果验证
随着分类器数目的增加，预测误差显著下降。
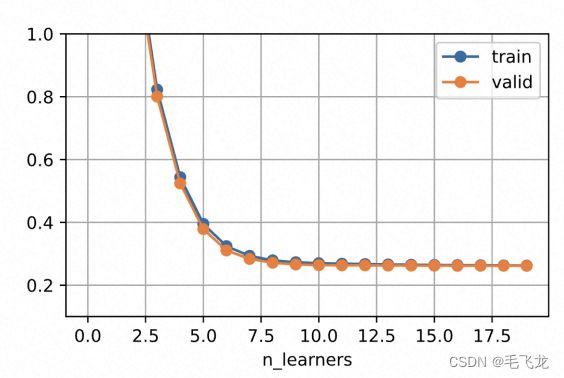图片来源：斯坦福大学2021秋季《实用机器学习课程》
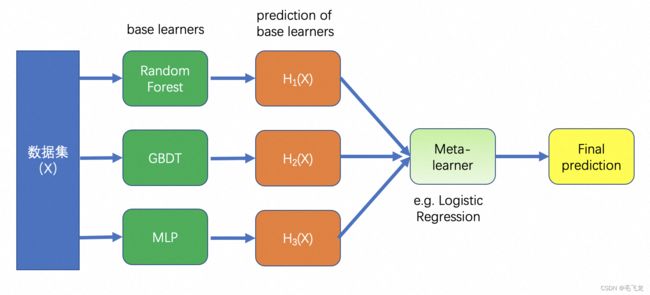
Stacking（同时降低偏差方差）
Stacking方法是算法竞赛利器，在不同的算法竞赛中被广泛应用，往往能得到最佳效果，最先在netfix的用户推荐算法竞赛中被运用，冠军获得者将其他参赛者的模型做了融合。与Bagging在不同数据集（随机放回采样结果）上训练同类型的模型，Stacking一般是在相同的数据集上训练不同类型的模型（base learner），然后基于base learner进行预测得到H(X)，再将H(X)作为特征输入Meta learner 进行二次训练，将base learner和meta learner合并在一起，作为最终的预测模型，过程如下：
算法描述如下：
上述为单层stacking方法，此外还有多层stacking方法，此处不作讨论。
效果验证
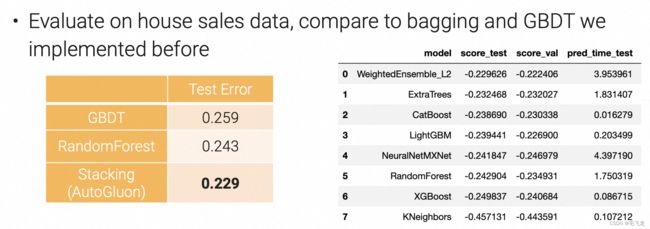图片来源：斯坦福大学2021秋季《实用机器学习课程》
可以看到，模型融合的效果确实比单个模型要好一点。
模型融合方法计算复杂度
| 模型融合方法 | 降低Bias | 降低Variance | 计算复杂度 | 并行度 |
|---|---|---|---|---|
| Bagging | Y | n | n | |
| Boosting | Y | n | 1 | |
| Stacking | Y | Y | n | n |
| k-fold MuliLayer Stacking | Y | Y | n * l *k | n*k |
其中l为stack layer层数，k为k-fold折数
参考
1. 斯坦福大学2021秋季实用机器学习课程，Syllabus — Practical Machine Learning
2. Kaggle机器学习之模型融合（stacking）心得 - 知乎
3. https://medium.com/@saugata.paul1010/ensemble-learning-bagging-boosting-stacking-and-cascading-classifiers-in-machine-learning-9c66cb271674
4.https://towardsdatascience.com/simple-model-stacking-explained-and-automated-1b54e4357916#:~:text=In%20model%20stacking%2C%20we%20don,a%20higher%2Dlevel%20meta%20model
5. BootstrapOutOfBag: A scikit-learn compatible version of the out-of-bag bootstrap - mlxtend