算法篇之二分
二分算法简介
特点
最简单的一种算法,也是最恶心,细节最多,最容易写出死循环的算法
时间复杂度O(logN)
如何学习
- 明白其中的算法原理,二分并不是只有数组有序的的时候使用,而是看是否具有二段性。
- 模板
- 朴素的二分模板(easy,有局限性)
- 查找左边界的二分模板
- 查找右边界的二分模板
b,c两种模板是万能模板,但是细节多
二分查找
题目链接:二分查找
算法思路:
代码
class Solution {
public int search(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
// 当left == right的时候还未判断
while(left <= right) {
int mid = left + (right - left) / 2;
if(nums[mid] < target) {
left = mid + 1;
}else if(nums[mid] > target) {
right = mid - 1;
}else {
return mid;
}
}
return -1;
}
}
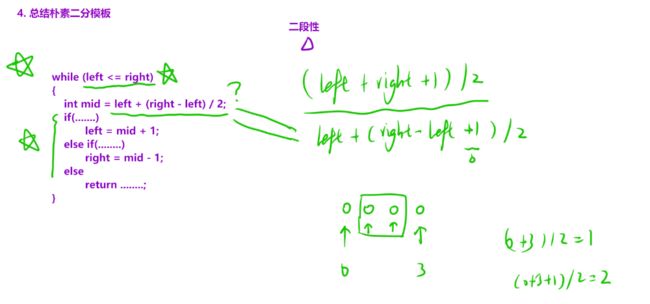
朴素二分模板
在排列数组中查找元素的第一个和最后一个位置
题目链接:在排列数组中查找元素的第一个和最后一个位置
算法思路
代码
class Solution {
public int[] searchRange(int[] nums, int target) {
int[] result = new int[2];
result[0] = result[1] = -1;
if(nums.length == 0) return result;
// 寻找区间左端点()
int left = 0, right = nums.length - 1;
// 1. left<=right会死循环,当left=right找到target时,进入循环还会走right=mid,一直循环下去。
// 2. 当left==right时就是答案,不需要再判断了
while(left < right) {
// 如果数组是偶数要取左边元素
// 因为取右边的元素会死循环,比如如果剩下(1,2)两个元素
// left=1,right=2,mid=2.更新区间后,left,right,mid的值没有改变
int mid = left + (right - left) / 2;
// 二段性,左区间小于target,右区间大于等于target
if(nums[mid] < target) {
left = mid + 1; // 由于左区间都是小于target,所以left=mid+1
}else {
right = mid;// 由于target在右区间间,所有right不能等于mid-1
}
}
if(nums[left] != target) return result;
result[0] = left;
// 寻找区间右端点
left = 0;
right = nums.length - 1;
while(left < right) {
// 如果数组是偶数要取右边元素
// 因为取左边的元素会死循环,比如如果剩下(1,2)两个元素
// left=1,right=2,mid=2.更新区间后,left,right,mid的值没有改变
int mid = left + (right - left + 1) / 2;
if(nums[mid] <= target) {
left = mid; // 由于左区间都是小于等于target,所以left不能等于mid+1
}else {
right = mid - 1; // 由于右区间都是小于target,所以right=mid-1
}
}
result[1] = left;
return result;
}
}
模板
搜索插入位置
题目链接:搜索插入位置
算法思路
数组是有序数组,具有二段性。可以将数组划分左右两个区间,左区间<=target,右区间>target。即可以套用求右端点模板。
代码
class Solution {
public int searchInsert(int[] nums, int target) {
// 利用二段性,可以划分为左区间<=target,右区间>target
// 也可以划分为左区间=target
// 咱们这里采用查找区间右端点模板
int left = 0, right = nums.length - 1;
while(left < right) {
int mid = left + (right - left + 1) / 2;
if(nums[mid] <= target) {
left = mid;
}else {
right = mid - 1;
}
}
if(nums[left] < target) return left + 1;
return left;
}
}
X的平方根
题目链接:X的平方根
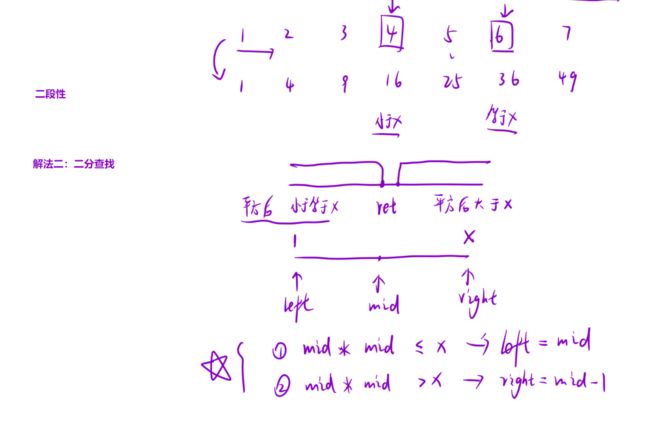
算法思路
代码:
class Solution {
public int mySqrt(int x) {
// x的平分根一定在0~x之间
long left = 0, right = x;
// 变成求mid*mid=x
// 因为保留整数部分,可以划分为左区间<=x,右区间>x
while(left < right) {
// 使用long,反溢出
long mid = left + (right - left + 1) / 2;
if(mid * mid <= x) {
left = mid;
}else {
right = mid - 1;
}
}
return (int)left;
}
}
山脉数组的峰顶索引
题目链接:山脉数组的峰顶索引
算法思路:
代码:
class Solution {
public int peakIndexInMountainArray(int[] arr) {
// 利用二段性,可以将区间分为小于等于峰值的左区间,小于峰值的右区间
// 即套用求区间右端点模板
int left = 0, right = arr.length - 1;
while(left < right) {
int mid = left + (right - left + 1) / 2;
if(arr[mid] > arr[mid - 1]) {
left = mid;
}else {
right = mid - 1;
}
}
return left;
}
}
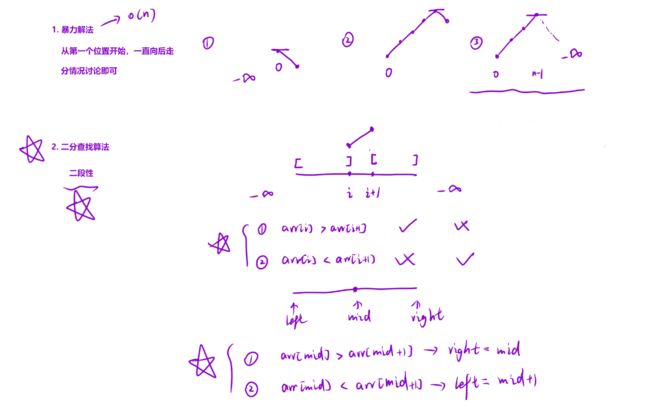
寻找峰值
题目链接:寻找峰值
算法思路:
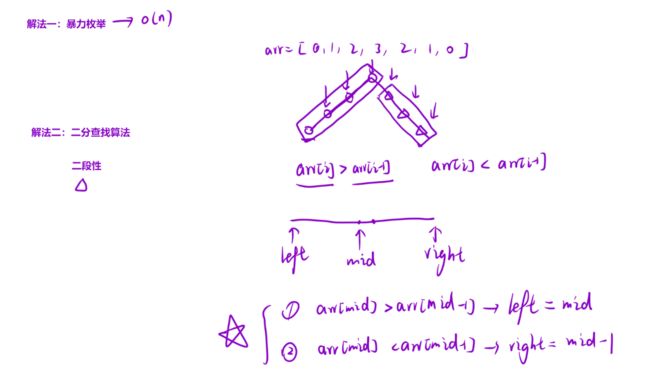
nums[i] > nums[i+1]:此时「左侧区域」⼀定会存在⼭峰(因为最左侧是负⽆ 穷),那么我们可以去左侧去寻找结果;nums[i] < nums[i+1]:此时「右侧区域」⼀定会存在⼭峰(因为最右侧是负⽆ 穷),那么我们可以去右侧去寻找结果;
代码:
class Solution {
public int findPeakElement(int[] nums) {
int left = 0, right = nums.length - 1;
while(left < right) {
int mid = left + (right - left) / 2;
if(nums[mid] > nums[mid + 1]) {
right = mid;
}else {
left = mid + 1;
}
}
return left;
}
}
寻找旋转排序数组中的最小值
题目链接:寻找旋转排序数组中的最小值
算法思路:
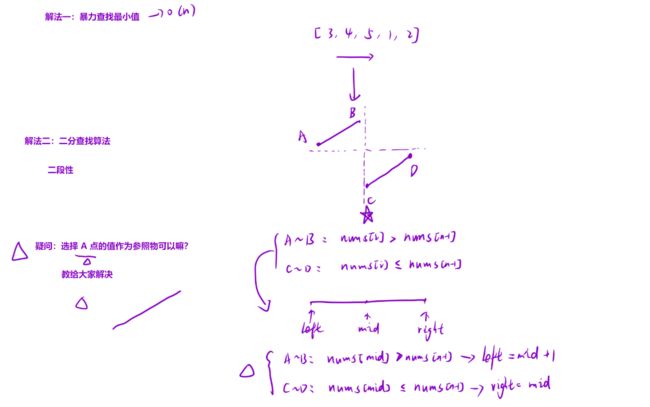
⼆分的本质:找到⼀个判断标准,使得查找区间能够⼀分为⼆。
通过图像我们可以发现, [A,B] 区间内的点都是严格⼤于 D 点的值的, C 点的值是严格小于 D 点的值的。但是当 [C,D] 区间只有⼀个元素的时候, C 点的值是可能等于 D 点的值的。
因此,初始化左右两个指针 left , right :
然后根据 mid 的落点,我们可以这样划分下⼀次查询的区间:
- 当 mid 在 [A,B] 区间的时候,也就是 mid 位置的值严格⼤于 D 点的值,下⼀次查询区间在 [mid + 1,right] 上;
- 当 mid 在 [C,D] 区间的时候,也就是 mid 位置的值严格⼩于等于 D 点的值,下次查询区间在 [left,mid] 上。
当区间⻓度变成 1 的时候,就是我们要找的结果。
代码:
class Solution {
public int findMin(int[] nums) {
int left = 0, right = nums.length - 1;
int n = nums.length;
while(left < right) {
int mid = left + (right - left) / 2;
if(nums[mid] > nums[n - 1]) {
left = mid + 1;
}else {
right = mid;
}
}
return nums[left];
}
}
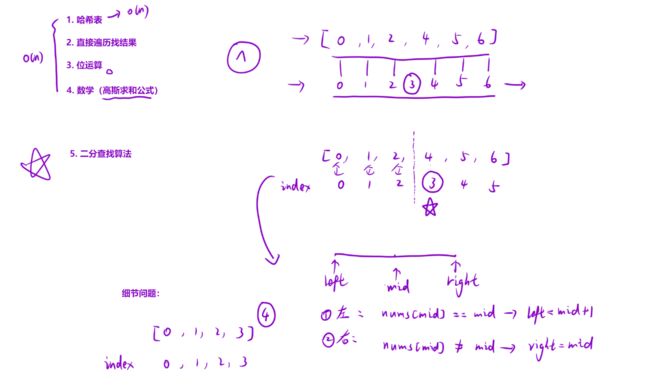
0到n-1中缺失的数字
题目链接:0到n-1中缺失的数字
算法思路:
- 在第⼀个缺失位置的左边,数组内的元素都是与数组的下标相等的;
- 在第⼀个缺失位置的右边,数组内的元素与数组下标是不相等的。
因此,我们可以利⽤这个「⼆段性」,来使⽤「⼆分查找」算法。
代码:
class Solution {
public int takeAttendance(int[] records) {
// 可以划分为左区间数值和下标相等,右区间数值和下标不相等
int left = 0, right = records.length - 1;
while(left < right) {
int mid = left + (right - left) / 2;
if(records[mid] == mid) {
left = mid + 1;
}else {
right = mid;
}
}
// 注意处理数组只有一个数的情况
return records[left] == left ? left + 1 : left;
}
}