算法&数据结构(2024/1/30)【线性表】
算法
1、算法是解决特定问题求解步骤的描述,在计算机中表现为指令的有限序列,并且每条指令表示一个或多个操作。
2、特性:输入、输出、有穷性、确定性和可行性。
有穷性:指算法在执行有限的步骤之后,自动结束而不会出现无限循环,并且每一个步骤在可接受的实践内完成。
确定性:算法的每一步骤都具有确定的含义,不会出现两种含义。
可行性:算法的每一步都必须是可行的(每一步能够通过执行有限次数完成)。
3、要求:正确性、可读性、健壮性以及时间效率高和存储量低。
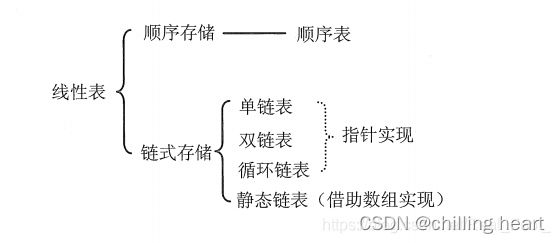
线性表(List)
1、定义:零个或多个数据元素的有效序列。(数据元素是有限的!!)
2、假设线性表的数据集合为 {a1,a2,…,an}
(1)其中除第一个元素a1外,每一个元素有且只有一个直接前驱元素,除了最后一个元素an外,每一个元素有且只有一个直接后继元素。
(2)a1是唯一的“第一个”元素,又称表头元素;an是唯一的“最后一个元素”,又称表尾元素。
(3)线性表元素个数为n个(线性表长度),当n=0时,此线性表为空表。
(4)在复杂的线性表中,一个数据元素可以由若干个数据项组成。
3、特点:
(1)表中元素个数有限的(有限序列)。
(2)表中元素具有逻辑上的顺序性,表中元素有其先后次序。
(3)表中元素都是数据元素,每个元素都是单个元素。
(4)数据元素的数据类型都相同,这意味着每个元素占有相同大小的存储空间。
(5)数据元素具有抽象性,即仅讨论元素间的逻辑关系,而不考虑元素究竟表示什么内容。
4、基本操作(抽象数据类型定义):
InitList(*L):初始化表,建立一个空的线性表L。
ListLength(L):求表长,返回线性表L的长度(线性表L元素的个数)。
LocateElem(L,e):在线性表中L查找与给定值e相等的元素,如果查找成功,返回该元素在表中的序号,表示成功;否则,返回0表示失败。
GetElem(L,i,*e):将线性表L中的第i个位置元素值返回给e。
ListInsert(*L,i,e):插入操作,在线性表L中的第i个位置上插入新元素e。
ListDelete(*L,i,*e):删除操作,删除线性表L中的第i个位置的元素,并用e返回删除元素的值。
PrintList(L):输出操作,按前后顺序输出线性表L的所有元素值。
ListEmpty(L):判断是否为空表,若线性表L为空表,则返回true;否则返回false。
DestroyList(&L):销毁操作,销毁线性表,并释放线性表L所占用的空间。
ClearList(*L):将线性表L清空。
5、
(1)数据元素之间的关系是一对一的关系。
(2)当你传递一个参数给函数时,这个参数是否会在函数内被改动决定了使用什么参数形式。
如果需要被改动,则需要传递指向这个参数的指针。
如果不需要被改动,则可以直接传递这个参数。
今日刷题
洛谷 p1165 日志分析
日志分析
题目描述
M 海运公司最近要对旗下仓库的货物进出情况进行统计。目前他们所拥有的唯一记录就是一个记录集装箱进出情况的日志。该日志记录了两类操作:第一类操作为集装箱入库操作,以及该次入库的集装箱重量;第二类操作为集装箱的出库操作。这些记录都严格按时间顺序排列。集装箱入库和出库的规则为先进后出,即每次出库操作出库的集装箱为当前在仓库里所有集装箱中最晚入库的集装箱。
出于分析目的,分析人员在日志中随机插入了若干第三类操作――查询操作。分析日志时,每遇到一次查询操作,都要报告出当前仓库中最大集装箱的重量。
输入格式:
包含N+1行:
第一行为一个正整数 N,对应于日志内所含操作的总数。
接下来的 N行,分别属于以下三种格式之一:
- 格式 1:0 X,表示一次集装箱入库操作,正整数 $X$ 表示该次入库的集装箱的重量。
- 格式 2:1,表示一次集装箱出库操作,(就当时而言)最后入库的集装箱出库。
- 格式 3:2,表示一次查询操作,要求分析程序输出当前仓库内最大集装箱的重量。
当仓库为空时你应该忽略出库操作,当仓库为空查询时你应该输出 0。
输出格式:
输出行数等于日志中查询操作的次数。每行为一个整数,表示查询结果。
样例输入
13
0 1
0 2
2
0 4
0 2
2
1
2
1
1
2
1
2
输出
2
4
4
1
0
提示:
数据范围及约定
- 对于 20%的数据,有 N <= 10;
- 对于 40%的数据,有 N <=1000;
- 对于 100%的数据,有 1 <= N <= 200000,1<= X <=10^8。代码如下:
#include
#include
#include //使用栈数据结构
using namespace std;
int n,m,x;
stacksta; //声明一个整型栈sta
int main()
{
scanf("%d",&n);
sta.push(0); //将0压入栈中,初始化为后面输入操作中准备
while(n--)
{
scanf("%d",&m);
if(m==0) //与栈顶元素进行比较,将较大值压入栈中
{
scanf("%d",&x);
sta.push(max(x,sta.top()));
}
if(m==1) //如果栈不为空,则弹出栈顶元素;否则继续下一次循环而不做任何操作
{
if(!sta.empty())
sta.pop();
else
continue;
}
if(m==2) //如果栈不为空,则数出栈顶元素,否则输出“0”,表示在某些情况下需要获取并输出栈顶元素
{
if(!sta.empty())
printf("%d\n",sta.top());
else
printf("0\n");
}
}
return 0;
}
希望今天的内容对大家有用! O(∩_∩)O