代码随想录算法训练营第二二天| 二叉搜索树的最近公共祖先、二叉搜索树中的插入操作、删除二叉搜索树中的节点

LeetCode 235. 二叉搜索树的最近公共祖先
LeetCode 701.二叉搜索树中的插入操作
LeetCode 450.删除二叉搜索树中的节点

二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

如果 中间节点是 q 和 p 的公共祖先，那么 中节点的数组 一定是在 [p, q]区间的。即 中节点 > p && 中节点 < q 或者 中节点 > q && 中节点 < p。

且当我们从上向下去递归遍历，第一次遇到 cur节点是数值在[q, p]区间中，那么cur就是 q和p的最近公共祖先。

p、q 为不同节点且均存在于给定的二叉搜索树中。→ 省去了判断是否为 null 的操作。

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
       
        // if (root == null) return root; // 因为p、q 为不同节点且均存在于给定的二叉搜索树中，所以不用判断
        // TreeNode left = lowestCommonAncestor(root.left, p, q); if (left != null) return left; // 因为p、q 为不同节点且均存在于给定的二叉搜索树中，所以不用判断
        if (root.val > p.val && root.val > q.val) return lowestCommonAncestor(root.left, p, q);
        if (root.val < p.val && root.val < q.val) return lowestCommonAncestor(root.right, p, q);
        return root;
    }
}

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        while (true) {
            if (root.val > p.val && root.val > q.val) {
                root = root.left;
            } else if (root.val < p.val && root.val < q.val) {
                root = root.right;
            } else {
                break;
            }
        }
        return root;
    }
}

二叉搜索树中的插入操作

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

只要遍历二叉搜索树，找到空节点 插入元素就可以了。

终止条件就是找到遍历的节点为null的时候，就是要插入节点的位置了，并把插入的节点返回。

这里把添加的节点返回给上一层，就完成了父子节点的赋值操作了。

把新的节点返回给上一层，上一层就要用 root->left 或者 root->right接住

class Solution {
    TreeNode pre = null;
    TreeNode cur = null;
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) {
            TreeNode node = new TreeNode(val);
            return node;
        }
        if (root.val > val) root.left = insertIntoBST(root.left, val);
        if (root.val < val) root.right = insertIntoBST(root.right, val);
        return root;
    }

}

class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) return new TreeNode(val);
        TreeNode newRoot = root;
        TreeNode pre = root;

        while (root != null) {
            pre = root;
            if (root.val > val) {
                root = root.left;
            } else if (root.val < val) {
                root = root.right;
            }
        }
        if (pre.val > val) {
            pre.left = new TreeNode(val);
        } else {
            pre.right = new TreeNode(val);
        }
        return newRoot;
    }
}

删除二叉搜索树中的节点

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；
如果找到了，删除它。

二叉搜索树中删除节点遇到的情况：

1. 没找到删除的节点，遍历到空节点直接返回

2. 找到删除的节点

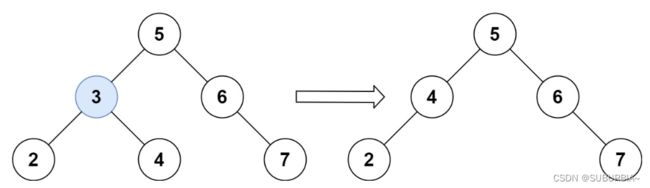
   2.1 左右孩子都为空（叶子节点）， 直接删除节点，返回 null 为根节点

   2.2 删除节点的左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点

   2.3 删除节点的右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点

   2.4 左右孩子节点都不为空，则将删除节点的左子树头结点（左孩子）放到删除节点的右子树的最左面节点的左孩子上，返回删除节点右孩子为新的根节点。

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) return root;  // 第一种情况：没找到删除的节点，遍历到空节点直接返回了
        if (root.val == key) {     // 内含第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回NULL为根节点
            if (root.left == null) {   // 第三种情况：其左孩子为空，右孩子不为空，删除节点，右孩子补位 ，返回右孩子为根节点
                return root.right;
            } else if (root.right == null) {  // 第四种情况：其右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
                return root.left;
            } else {
            // 第五种情况：左右孩子节点都不为空，则将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子的位置
            // 并返回删除节点右孩子为新的根节点。
                TreeNode cur = root.right;   // 找右子树最左面的节点
                while (cur.left != null) {
                    cur = cur.left;
                }
                cur.left = root.left;   // 把要删除的节点（root）左子树放在cur的左孩子的位置
                root = root.right;      // 返回旧root的右孩子作为新root
                return root;
            }
        }
        if (root.val > key) root.left = deleteNode(root.left, key);
        if (root.val < key) root.right = deleteNode(root.right, key);
        return root;
    }
}

二叉搜索树添加节点只需要在叶子上添加就可以的，不涉及到结构的调整，而删除节点操作涉及到结构的调整。

普通二叉树的删除方式

普通二叉树的删除方式（没有使用搜索树的特性，遍历整棵树），用交换值的操作来删除目标节点。

代码中目标节点（要删除的节点）被操作了两次：

第一次是和目标节点的右子树最左面节点交换。

第二次直接被NULL覆盖了。

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        root = delete(root,key);
        return root;
    }

    private TreeNode delete(TreeNode root, int key) {
        if (root == null) return null;

        if (root.val > key) {
            root.left = delete(root.left,key);
        } else if (root.val < key) {
            root.right = delete(root.right,key);
        } else {
            if (root.left == null) return root.right;
            if (root.right == null) return root.left;
            TreeNode tmp = root.right;
            while (tmp.left != null) {
                tmp = tmp.left;
            }
            root.val = tmp.val;
            root.right = delete(root.right,tmp.val);
        }
        return root;
    }
}