C++迷宫游戏详解
个人主页:[PingdiGuo_guo]
收录专栏:[C++干货专栏]
大家好呀,我是PingdiGuo_guo,今天我们来学习用C++实现一个迷宫游戏。
目录
1.迷宫的具体步骤
1.1.迷宫的初始化
1.2.寻路算法
1.DFS算法
2.BFS算法
1.3.移动
2.总结
C++迷宫游戏的实现需要考虑迷宫的表示方式、寻路算法以及代码实现。在本篇博客中,我们将逐步实现一个C++迷宫游戏。
1.迷宫的具体步骤
1.迷宫的初始化:包括选择难度,随机生成迷宫,以及玩家移动后的迷宫
2.寻路算法:在迷宫中,我们需要一个正确的算法来判断当前路径是否正确
3.移动:玩家可以按w,a,s,d键来实现移动
1.1.迷宫的初始化
迷宫的初始化具体实现步骤如下:
1. 包含所需的头文件
2. 使用命名空间 std。
3. 声明迷宫的相关常量,如空格、墙、路径、起点和终点的字符。
4. 声明随机数生成器 gen。
5. 声明迷宫的宽度和高度变量。
6. 声明迷宫的二维字符向量 cells。
7. 声明起点和终点的位置变量。
8. 实现函数 generateMaze() 用于生成随机迷宫。
- 使用随机数生成器生成起点和终点的随机位置。
- 遍历迷宫的每个位置,根据一定的概率生成墙或路径,并将起点和终点的字符设置为对应的字符。
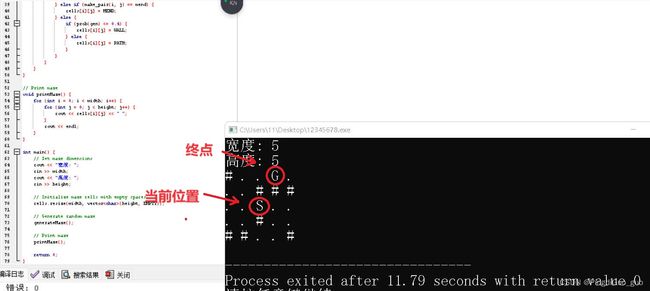
9. 实现函数 printMaze() 用于打印迷宫。
- 遍历迷宫的每个位置,打印对应的字符。
10. 在 main() 函数中:
- 提示用户输入迷宫的宽度和高度。
- 调整 cells 的大小为指定的宽度和高度,并初始化为空格字符。
- 生成随机迷宫。
- 打印迷宫。
11. 返回 0,表示程序成功执行完毕。
以下是具体的代码实现:
#include
using namespace std;
// Maze cell types
const char EMPTY = ' ';
const char WALL = '#';
const char PATH = '.';
const char START = 'S';
const char MEND = 'G';
// Random number generator
random_device rd;
mt19937 gen(rd());
// Maze dimensions
int width, height;
// Maze grid
vector> cells;
// Start and end positions
pair start, mend;
// Generate random maze
void generateMaze() {
// Set start and end points randomly
uniform_int_distribution<> dis(0, width - 1);
start = make_pair(dis(gen), dis(gen));
mend = make_pair(dis(gen), dis(gen));
// Generate empty cells with 40% walls
uniform_real_distribution prob(0.0, 1.0);
for (int i = 0; i < width; i++) {
for (int j = 0; j < height; j++) {
if (make_pair(i, j) == start) {
cells[i][j] = START;
} else if (make_pair(i, j) == mend) {
cells[i][j] = MEND;
} else {
if (prob(gen) <= 0.4) {
cells[i][j] = WALL;
} else {
cells[i][j] = PATH;
}
}
}
}
}
// Print maze
void printMaze() {
for (int i = 0; i < width; i++) {
for (int j = 0; j < height; j++) {
cout << cells[i][j] << " ";
}
cout << endl;
}
}
int main() {
// Set maze dimensions
cout << "宽度: ";
cin >> width;
cout << "高度: ";
cin >> height;
// Initialize maze cells with empty spaces
cells.resize(width, vector(height, EMPTY));
// Generate random maze
generateMaze();
// Print maze
printMaze();
return 0;
}
1.2.寻路算法
接下来,我们需要选择一个最优的寻路算法。在迷宫游戏中,常用的寻路算法有深度优先搜索(DFS)和广度优先搜索(BFS)。这两种算法都可以用于寻找迷宫的路径,但适用的场景和复杂度略有不同。
1.DFS算法
DFS算法通过递归的方式进行搜索,每次都先选择一个方向前进,直到无法前进为止,然后回溯到上一个节点继续搜索。DFS算法的复杂度为O(V + E),其中V是节点的数量,E是边的数量。我们可以分析出具体步骤:
1. 定义一个名为DFS的函数,接收当前位置的坐标x和y作为参数,并返回一个布尔值。
2. 首先,判断当前位置是否超出了迷宫的边界,如果是,则返回false。
3. 接着,判断当前位置是否为墙壁(用'#'表示),如果是,则返回false。
4. 然后,判断当前位置是否为终点(用'G'表示),如果是,则返回true,表示已经找到了一条通路。
5. 如果以上条件都不满足,说明当前位置是可走的空地(用'.'表示),将当前位置标记为已访问(用'#'代替原来的空地)。
6. 通过递归调用DFS函数,按照上、下、左、右的顺序尝试前进,即DFS(x + 1, y)、DFS(x - 1, y)、DFS(x, y + 1)、DFS(x, y - 1)。
7. 如果在某个方向上的递归调用返回true,表示找到了通路,则返回true。
8. 如果以上递归调用都没有找到通路,则说明当前位置不是通路,将当前位置标记为未访问(用' '代替原来的'#'),进行回溯。
9. 最后,返回false,表示没有找到通路。
通过以上步骤,使用DFS算法可以在迷宫中寻找通路。
以下是具体的代码实现:
bool DFS(int x, int y) {
if (x < 0 || x >= N || y < 0 || y >= N) {
return false;
}
if (maze[x][y] == '#') {
return false;
}
if (maze[x][y] == 'G') {
return true;
}
maze[x][y] = '#'; // 标记为已访问
if (DFS(x + 1, y) || DFS(x - 1, y) || DFS(x, y + 1) || DFS(x, y - 1)) {
return true;
}
maze[x][y] = '.'; // 回溯,标记为未访问
return false;
}
2.BFS算法
BFS算法使用队列来存储待访问的节点,每次都从队列中取出一个节点进行访问,并将其周围的节点加入队列。BFS算法的复杂度为O(V + E),其中V是节点的数量,E是边的数量。我们可以分析出以下步骤:
1. 定义一个名为BFS的函数,接收起始位置的坐标x和y作为参数,并返回一个布尔值。
2. 创建一个队列(queue),并将起始位置加入队列中。
3. 使用while循环,当队列不为空时执行循环。
4. 在循环中,首先从队列中取出队首元素,即当前位置的坐标。
5. 接着,判断当前位置是否超出了迷宫的边界,如果是,则继续下一次循环。
6. 然后,判断当前位置是否为墙壁(用'#'表示),如果是,则继续下一次循环。
7. 接着,判断当前位置是否为终点(用'G'表示),如果是,则返回true,表示已经找到了一条通路。
8. 若以上条件都不满足,说明当前位置是可走的空地(用'.'表示),将当前位置标记为已访问(用'#'代替原来的空地)。
9. 将当前位置的上、下、左、右四个方向的相邻坐标加入队列中,即({x + 1, y})、({x - 1, y})、({x, y + 1})、({x, y - 1})。
10. 循环结束后,说明队列已经为空且没有找到通路,返回false。
通过以上步骤,使用BFS算法可以在迷宫中寻找通路。
bool BFS(int x, int y) {
queue> q;
q.push({x, y});
while (!q.empty()) {
pair curr = q.front();
q.pop();
int x = curr.first;
int y = curr.second;
if (x < 0 || x >= N || y < 0 || y >= N) {
continue;
}
if (maze[x][y] == '#') {
continue;
}
if (maze[x][y] == 'G') {
return true;
}
maze[x][y] = '#'; // 标记为已访问
q.push({x + 1, y});
q.push({x - 1, y});
q.push({x, y + 1});
q.push({x, y - 1});
}
return false;
} 1.3.移动
在迷宫游戏中,玩家需要根据输入的指令来移动。常见的移动指令有上、下、左、右四个方向。我们可以通过更新玩家的坐标来实现移动。我们可以分析出以下步骤:
1. 定义一个名为movePlayer的函数,接收玩家当前位置的坐标x和y的引用,以及移动的方向direction作为参数,并返回一个布尔值。
2. 根据输入的方向指令,使用条件判断来判断移动的方向。如果是"W"或"w",则判断玩家上方的位置是否为墙壁,如果不是,则更新玩家的坐标x减1;如果是"S"或"s",则判断玩家下方的位置是否为墙壁,如果不是,则更新玩家的坐标x加1;如果是"A"或"a",则判断玩家左边的位置是否为墙壁,如果不是,则更新玩家的坐标y减1;如果是"D"或"d",则判断玩家右边的位置是否为墙壁,如果不是,则更新玩家的坐标y加1。
3. 如果输入的方向指令不是以上四种有效指令,则返回false,表示无效指令。
4. 在玩家移动后,返回true,表示移动成功。
在主函数中,使用DFS算法找到了一条路径后,可以进入游戏循环。循环中,首先打印迷宫,然后提示玩家输入移动指令(W上,S下,A左,D右)或者Q退出。根据玩家输入的指令调用movePlayer函数来移动玩家,并判断是否成功找到出口。如果玩家输入Q,则跳出循环,游戏结束。
通过以上步骤,玩家可以在迷宫中根据输入指令进行移动,并且在找到出口时会进行相应的提示。
具体代码实现:
bool movePlayer(int& x, int& y, char direction) {
// 根据指令更新玩家的坐标
if (direction == 'W' || direction == 'w') { // 上
if (maze[x - 1][y] != '#') {
x--;
}
} else if (direction == 'S' || direction == 's') { // 下
if (maze[x + 1][y] != '#') {
x++;
}
} else if (direction == 'A' || direction == 'a') { // 左
if (maze[x][y - 1] != '#') {
y--;
}
} else if (direction == 'D' || direction == 'd') { // 右
if (maze[x][y + 1] != '#') {
y++;
}
} else {
return false; // 无效指令
}
return true;
}
在主函数中,我们可以在寻路算法之后添加以下代码,以实现玩家的移动:
// 使用DFS算法寻找路径
bool found = DFS(startX, startY);
if (found) {
cout << "找到了一条路径!" << endl;
cout << "请开始游戏!" << endl;
char direction;
while (true) {
printMaze(startX, startY); // 打印迷宫
cout << "请输入指令(W上, S下, A左, D右)或者Q退出:" << endl;
cin >> direction;
if (direction == 'Q' || direction == 'q') {
break;
}
movePlayer(startX, startY, direction); // 移动玩家
if (startX == endX && startY == endY) {
cout << "恭喜你成功找到出口!" << endl;
break;
}
}
} else {
cout << "没有找到路径!" << endl;
}上述代码通过循环接受玩家的输入指令,并根据指令更新玩家的坐标,实现玩家在迷宫中的移动。当玩家到达终点时,游戏结束。
2.总结
本篇博客讲解了实现迷宫的几个步骤与代码,希望大家有所收获。感谢大家的支持与观看,如果有好的建议欢迎留言!