二叉树相关力扣题目
二叉树的中序遍历
给定一个二叉树的根节点 root ，返回它的 中序 遍历。
示例 1：
输入：root = [1,null,2,3]
输出：[1,3,2]
示例 2：
输入：root = []
输出：[]
示例 3：
输入：root = [1]
输出：[1]
示例 4：
输入：root = [1,2]
输出：[2,1]
示例 5：
输入：root = [1,null,2]
输出：[1,2]
提示：
树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/binary-tree-inorder-traversal
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
思路
这题用递归就直接中序遍历就好了。
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> ans = new ArrayList<>();
inorder(root, ans);
return ans;
}
public void inorder(TreeNode root, List<Integer> ans) {
if (root == null) {
return;
}
inorder(root.left, ans);
ans.add(root.val);
inorder(root.right, ans);
}
}
迭代的写法
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
LinkedList<TreeNode> list = new LinkedList<>();
List<Integer> ans = new ArrayList<>();
while (!list.isEmpty() || root != null) {
while (root != null) {
list.addLast(root);
root = root.left;
}
TreeNode cur = list.removeLast();
ans.add(cur.val);
root = cur.right;
}
return ans;
}
}
二叉树的前序遍历
这题就不用简介了吧
代码
这里只放迭代做法
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
LinkedList<TreeNode> list = new LinkedList<>();
List<Integer> ans = new ArrayList<>();
while (!list.isEmpty() || root != null) {
while (root != null) {
ans.add(root.val);
list.addLast(root);
root = root.left;
}
TreeNode cur = list.removeLast();
root = cur.right;
}
return ans;
}
}
二叉树的后序遍历
同样不需要简介了吧
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> ans = new ArrayList<>();
LinkedList<TreeNode> list = new LinkedList<>();
TreeNode prev = null;
while (!list.isEmpty() || root != null) {
while (root != null) {
list.addLast(root);
root = root.left;
}
root = list.removeLast();
if (root.right == null || root.right == prev) {
ans.add(root.val);
prev = root;
root = null;
} else {
list.addLast(root);
root = root.right;
}
}
return ans;
}
}
不同的二叉搜索树
给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。
示例 1：
输入：n = 3
输出：5
示例 2：
输入：n = 1
输出：1
提示：
1 <= n <= 19
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/unique-binary-search-trees
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
思路
这题要用动态规划来做，状态的定义是长度为i的序列能构成的二叉搜索树的个数。
题目要求是计算不同二叉搜索树的个数。为此，我们可以定义两个函数：
G(n): 长度为 n 的序列能构成的不同二叉搜索树的个数。
F(i,n): 以 i 为根、序列长度为 n 的不同二叉搜索树个数 (1≤i≤n)。
可见，G(n) 是我们求解需要的函数。
稍后我们将看到，G(n)可以从 F(i,n) 得到，而 F(i,n) 又会递归地依赖于 G(n)。
首先，根据上一节中的思路，不同的二叉搜索树的总数 G(n)，是对遍历所有 i (1≤i≤n) 的 F(i,n)之和。换言之：
G(n)=∑i=1nF(i,n)
对于边界情况，当序列长度为 111（只有根）或为 000（空树）时，只有一种情况，即：
G(0)=1,G(1)=1
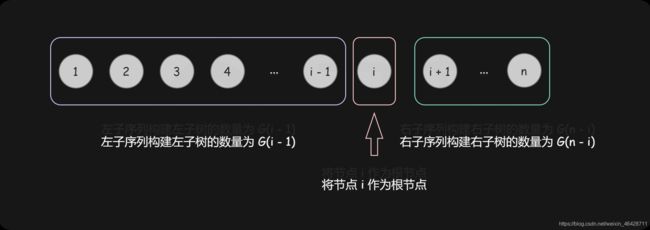
给定序列 1⋯n，我们选择数字 i 作为根，则根为 i 的所有二叉搜索树的集合是左子树集合和右子树集合的笛卡尔积，对于笛卡尔积中的每个元素，加上根节点之后形成完整的二叉搜索树，如下图所示：
作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/unique-binary-search-trees/solution/bu-tong-de-er-cha-sou-suo-shu-by-leetcode-solution/
来源：力扣（LeetCode） 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
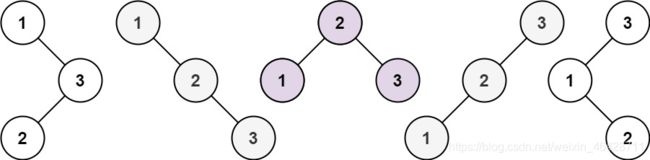
这里解释一下为什么G（n）会是G（i - 1）和G（n - i）的乘积的累加和。
以长度为3的时候举例，我们分别以1，2，3三个节点作为根节点来做二叉搜索树，当以1为根节点的时候，左子树为空，所以是G（0），右子树高度为2，所以是G（2），后面的同理。我们要把这三种情况相加起来才会得到长度为3的序列时二叉搜索树的所有情况。
代码
class Solution {
public int numTrees(int n) {
int[] dp = new int[n + 1];
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
for (int j = 1; j <= i; j++) {
dp[i] += dp[j - 1] * dp[i - j];
}
}
return dp[n];
}
}
验证二叉搜索树
给定一个二叉树，判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征：
节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:
2
/
1 3
输出: true
示例 2:
输入:
5
/
1 4
/
3 6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
根节点的值为 5 ，但是其右子节点值为 4 。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/validate-binary-search-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
思路
这题思路用的是dfs
我们递归的时候始终记录两个值，上限以及下限。在递归中不断地更新这两个值。
二叉搜索树的特点是左子树总是比根节点小，右子树总是比根节点大。而二叉搜索树的子树同样也是二叉搜索树，所以利用这点我们可以不断地判断根节点上一次递归中传递下来的上限和下限作比较，如果大于上限或者小于下限说明就不是二叉搜索树。
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isValidBST(TreeNode root) {
return dfs(root, Long.MAX_VALUE, Long.MIN_VALUE);
}
public boolean dfs(TreeNode root, long high, long low) {
if (root == null) {
return true;
}
if (root.val >= high || root.val <= low) {
return false;
}
return dfs(root.left, root.val, low) && dfs(root.right, high, root.val);
}
}
这里补充说明下，这题很坑的是他的测试用例会用到非常大，所以定义的时候不能用Integer.MAX_VALUE，只能用Long.MAX_VALUE，最小值也是同理。
对称二叉树
给定一个二叉树，检查它是否是镜像对称的。
例如，二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/
2 2
/ \ /
3 4 4 3
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1
/
2 2
\
3 3
进阶：
你可以运用递归和迭代两种方法解决这个问题吗？
来源：力扣（LeetCode） 链接：https://leetcode-cn.com/problems/symmetric-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
思路
这题迭代的思路就是用一个队列来存放遍历到的左右子树，具体逻辑是这样的。我们先存放两次根节点，将第一次存放的根节点作为左子树来进行遍历，第二次存放的根节点作为右子树来遍历。接下来遍历的过程就如代码所示，不断地添加新的子树进入队列，判断它们的值是否相同从而得出结论
这题递归的思路和迭代是一样的。判断部分的内容是完全一样的，不同的地方就在于迭代在判断完之后需要自己手动将接下来要遍历的左右子树添加进队列，而递归就可以直接调用方法。
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isSymmetric(TreeNode root) {
if (root == null) {
return true;
}
LinkedList<TreeNode> list = new LinkedList<>();
list.addLast(root);
list.addLast(root);
while (!list.isEmpty()) {
TreeNode temp = list.removeLast();
TreeNode righttemp = list.removeLast();
if (temp == null && righttemp == null) {
continue;
}
if (temp == null || righttemp == null || temp.val != righttemp.val) {
return false;
}
list.addLast(temp.left);
list.addLast(righttemp.right);
list.addLast(temp.right);
list.addLast(righttemp.left);
}
return true;
}
}
递归的代码：
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isSymmetric(TreeNode root) {
return dfs(root.left, root.right);
}
public boolean dfs(TreeNode left,TreeNode right) {
if (left == null && right == null) {
return true;
}
if (left == null || right == null || left.val != right.val) {
return false;
}
return dfs(left.right, right.left) && dfs(left.left, right.right);
}
}
二叉树的层序遍历
给你一个二叉树，请你返回其按 层序遍历 得到的节点值。 （即逐层地，从左到右访问所有节点）。
示例：
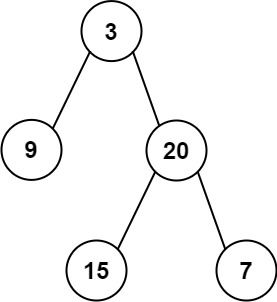
二叉树：[3,9,20,null,null,15,7],
3
/
9 20
/
15 7
返回其层序遍历结果：
[
[3],
[9,20],
[15,7]
]
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/binary-tree-level-order-traversal
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
思路
思路就是用队列存放每一层的树节点，在遍历一层的时候先求当前队列的长度，队列的长度就是本层树节点的数量。提前记录下来防止在接下来的遍历时不断地往队列中添加树节点的过程中遍历到了下一层的树节点。
需要注意的是这里不是先入后出而是先入先出。
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
LinkedList<TreeNode> queue = new LinkedList<>();
List<List<Integer>> ans = new ArrayList<List<Integer>>();
if (root == null) {
return ans;
}
queue.addLast(root);
while (!queue.isEmpty()) {
int currentsize = queue.size();
List<Integer> now = new ArrayList<>();
for (int i = 0; i < currentsize; i++) {
TreeNode temp = queue.removeFirst();
now.add(temp.val);
if (temp.left != null) {
queue.addLast(temp.left);
}
if (temp.right != null) {
queue.addLast(temp.right);
}
}
ans.add(now);
}
return ans;
}
}
二叉树的最大深度
给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例：
给定二叉树 [3,9,20,null,null,15,7]，
3
/
9 20
/
15 7
返回它的最大深度 3 。
思路
思路是用递归来做，我们递归根节点的左右子树，分别计算出左右子树的高度。
计算子树的高度过程是这样的，当我们遍历到空节点的时候，说明这颗子树已经到底，所以我们返回深度0，然后在他的上一层我们就会接收到这个深度0的数据，然后加上本层提供的高度1。
以只有一个节点的树作为例子计算，我们开始递归的时候，传入根节点的左右子树，在第二层的递归里，因为传递的子树为空，所以我们返回0。于是在第一层的递归里，我们接受到的lefthigh和righthigh都是0，接下来我们就取左右子树的最大高度0加上这个节点本身提供的高度1作为答案，也就是1
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int maxDepth(TreeNode root) {
return depth(root);
}
public int depth(TreeNode root) {
if (root == null) {
return 0;
}
int lefthigh = depth(root.left);
int righthigh = depth(root.right);
return Math.max(lefthigh, righthigh) + 1;
}
}
二叉树展开为链表
给你二叉树的根结点 root ，请你将它展开为一个单链表：
展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。
示例 1：
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]
示例 2：
输入：root = []
输出：[]
示例 3：
输入：root = [0]
输出：[0]
提示：
树中结点数在范围 [0, 2000] 内
-100 <= Node.val <= 100
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/flatten-binary-tree-to-linked-list
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
思路
首先考虑这题需要的是记录树的先序遍历的结果，我们考虑用一个list来存放树先序遍历的结果。然后按顺序取出这个list集合，然后将对应的节点的右节点改为集合中下一个数据即可。
具体到递归方法来做，我们就是要递归的去先序遍历树，然后将结果存放入list集合里面。
具体到迭代方法来做，我们就是要将先序遍历的过程通过队列来实现。
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public void flatten(TreeNode root) {
List<TreeNode> list = new ArrayList<>();
dfs(root, list);
int listsize = list.size();
for (int i = 1; i < listsize; i++) {
TreeNode temp = list.get(i - 1);
temp.left = null;
temp.right = list.get(i);
}
}
public void dfs(TreeNode root, List<TreeNode> list) {
if (root == null) {
return;
}
list.add(root);
dfs(root.left, list);
dfs(root.right, list);
}
}
迭代做法
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public void flatten(TreeNode root) {
List<TreeNode> ans = new ArrayList<>();
LinkedList<TreeNode> queue = new LinkedList<>();
//queue.addLast(root);
while (!queue.isEmpty() || root != null) {
if (root != null) {
queue.addLast(root);
ans.add(root);
root = root.left;
} else {
root = queue.removeLast();
root = root.right;
}
}
int cur = ans.size();
for (int i = 1; i < cur; i++) {
TreeNode temp = ans.get(i - 1);
temp.left = null;
temp.right = ans.get(i);
}
}
}
二叉树的最大路径和
路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ，返回其 最大路径和 。
示例 1：
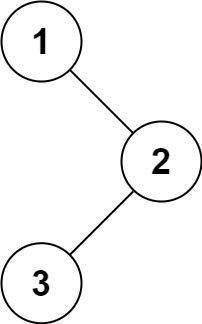
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6
示例 2：
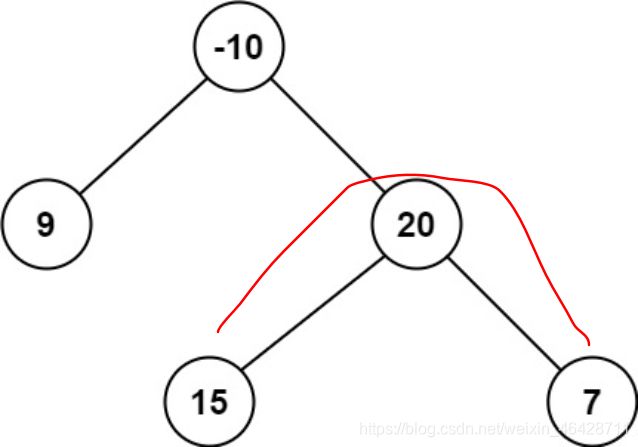
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42
提示：
树中节点数目范围是 [1, 3 * 104]
-1000 <= Node.val <= 1000
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/binary-tree-maximum-path-sum
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
思路
递归调用，每次比对该节点能获得到的最大路径和和当前的最大和，如果较大就替换当前的最大和。
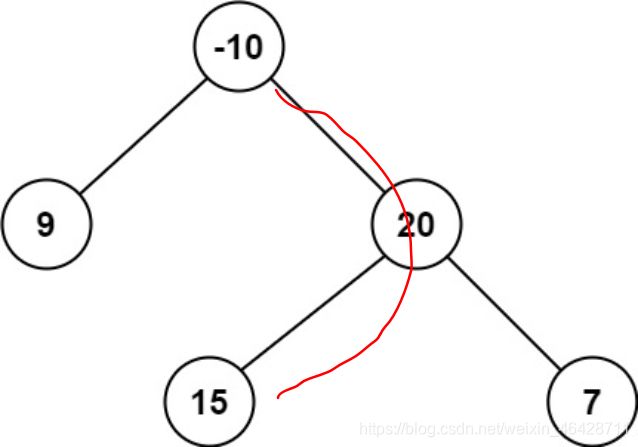
这里需要注意的一点是，我们需要的最大路径和是单条路径的，所以说我们在递归方法的return中只能取左子树或右子树中的最大值加上当前节点的值作为这个节点上的返回值。这是因为如果我们左右子树都加上的话，那么就不是一条路径了。如下图
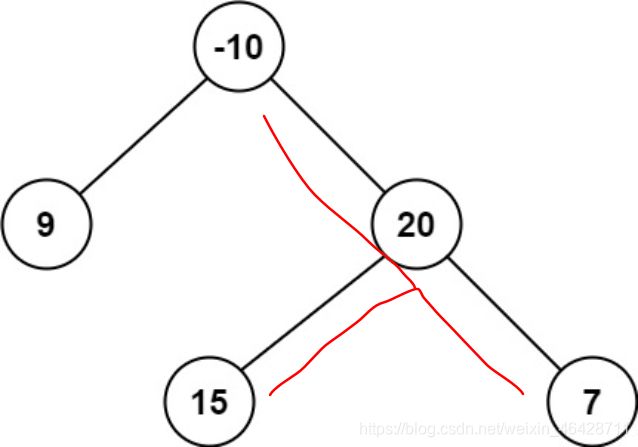
可以看到如果在20这个结点的时候左右子树都加上，那么返回到-10这个节点的时候就已经不是一个路径了。
所以我们只能是下面两个情况中的一种
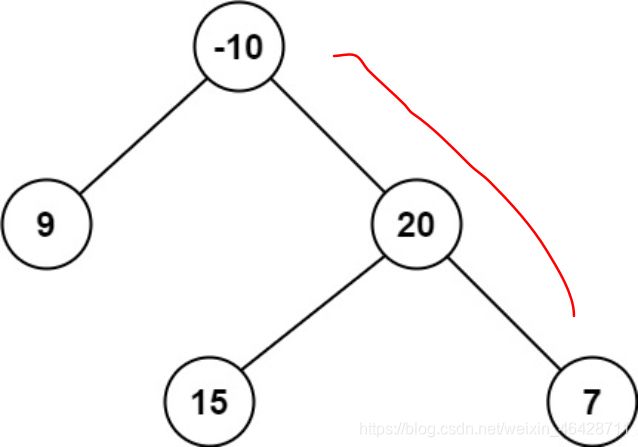
或者是
而在计算当前节点的最大路径和的时候是可以添加上两个子树的值的，这是因为在这种情况下仍属于一个路径。
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
int ans = Integer.MIN_VALUE;
public int maxPathSum(TreeNode root) {
maxp(root);
return ans;
}
public int maxp(TreeNode root) {
if (root == null) {
return 0;
}
int leftmax = Math.max(0, maxp(root.left));
int rightmax = Math.max(0, maxp(root.right));
int nowmax = root.val + leftmax + rightmax;
ans = Math.max(ans, nowmax);
return root.val + Math.max(leftmax, rightmax);
}
}
翻转二叉树
翻转一棵二叉树。
示例：
输入：
4
/
2 7
/ \ /
1 3 6 9
输出：
4
/
7 2
/ \ /
9 6 3 1
来源：力扣（LeetCode） 链接：https://leetcode-cn.com/problems/invert-binary-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
思路
这题用递归来做的话，就是先不断地调用递归方法到最下面的叶子节点，叶子节点返回null回去，然后上面的节点1将两个叶子节点交换之后再返回上去，节点2的操作也类似。接下来再上面一层的节点3将下面一层的节点1和节点2给交换再返回更上层的节点。
这题用迭代来做的话，就是不断取出队列中的节点，然后交换左右子树，接下来把这个节点非空的子树存进队列即可
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return null;
}
TreeNode lefttree = invertTree(root.left);
TreeNode rightree = invertTree(root.right);
root.left = rightree;
root.right = lefttree;
return root;
}
}
迭代做法
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode invertTree(TreeNode root) {
LinkedList<TreeNode> list = new LinkedList<>();
if (root == null) {
return null;
}
list.addLast(root);
while (!list.isEmpty()) {
TreeNode node = list.removeLast();
TreeNode temp = node.left;
node.left = node.right;
node.right = temp;
if (node.left != null) {
list.addFirst(node.left);
}
if (node.right != null) {
list.addFirst(node.right);
}
}
return root;
}
}
二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”
示例 1：
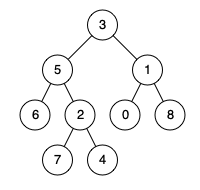
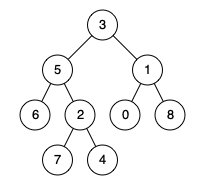
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2：
示例 3：
输入：root = [1,2], p = 1, q = 2
输出：1
提示：
树中节点数目在范围 [2, 105] 内。
-109 <= Node.val <= 109
所有 Node.val 互不相同 。
p != q
p 和 q 均存在于给定的二叉树中。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
思路
这题的思路没那么清晰，摘要一部分题解大佬的解释
根据以上定义，若 rootrootroot 是 p,qp, qp,q 的 最近公共祖先 ，则只可能为以下情况之一：
p 和 q 在 rootr 的子树中，且分列 root 的 异侧（即分别在左、右子树中）；
p=root ，且 q 在 roott 的左或右子树中；
q=root，且 p 在 root 的左或右子树中；
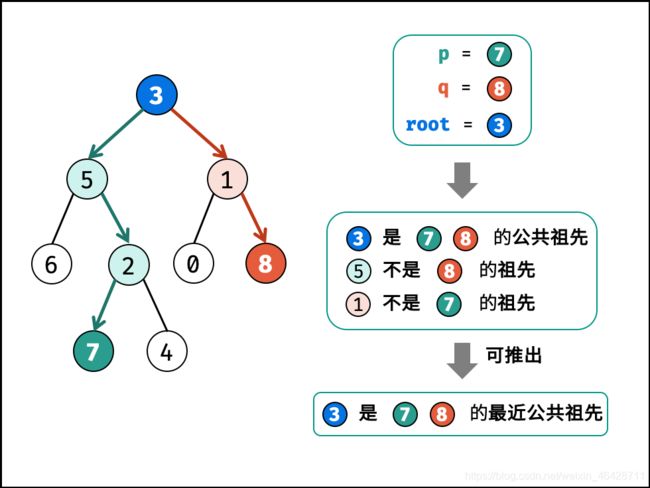
考虑通过递归对二叉树进行先序遍历，当遇到节点 p 或 q 时返回。从底至顶回溯，当节点 p,q 在节点 root 的异侧时，节点 root 即为最近公共祖先，则向上返回 root 。
作者：jyd
链接：https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree/solution/236-er-cha-shu-de-zui-jin-gong-gong-zu-xian-hou-xu/
来源：力扣（LeetCode） 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null || root == p || root == q) {
return root;
}
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if (left == null && right == null) {
return null;
}
if (left == null) {
return right;
}
if (right == null) {
return left;
}
return root;
}
}
二叉树的序列化与反序列化
序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。
请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。
提示: 输入输出格式与 LeetCode 目前使用的方式一致，详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式，你也可以采用其他的方法解决这个问题。
示例 1：
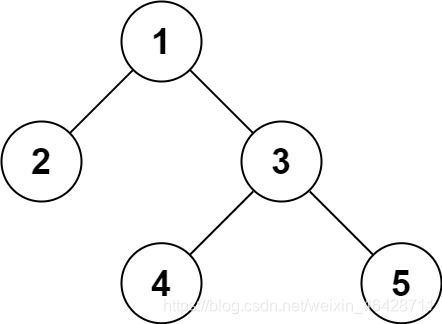输入：root = [1,2,3,null,null,4,5]
输出：[1,2,3,null,null,4,5]
示例 2：
输入：root = []
输出：[]
示例 3：
输入：root = [1]
输出：[1]
示例 4：
输入：root = [1,2]
输出：[1,2]
提示：
树中结点数在范围 [0, 104] 内
-1000 <= Node.val <= 1000
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/serialize-and-deserialize-binary-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
思路
这题的思路是这样的
序列化的时候，我们按层序遍历的顺序，一边遍历一边将下一层的节点存入list中，判断获取到的节点是否为空，将其数据按顺序存入builder中。
反序列化的时候，我们按照顺序来构造树，这里比较难理解的是i的使用，我们这里的i指针始终是指向当前建立的节点的左右子树，当理解这里之后代码就很清晰了。
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Codec {
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
if (root == null) {
return "[]";
}
StringBuilder builder = new StringBuilder();
LinkedList<TreeNode> list = new LinkedList<>();
builder.append("[");
list.addLast(root);
while (!list.isEmpty()) {
TreeNode node = list.removeFirst();
if (node != null) {
builder.append(node.val).append(",");
list.addLast(node.left);
list.addLast(node.right);
} else {
builder.append("null,");
}
}
builder.deleteCharAt(builder.length() - 1);
builder.append("]");
return builder.toString();
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
if (data == "[]") {
return null;
}
String[] array = data.substring(1, data.length() - 1).split(",");
TreeNode root = new TreeNode(Integer.valueOf(array[0]));
LinkedList<TreeNode> list = new LinkedList<>();
list.addLast(root);
int i = 1;
while (!list.isEmpty()) {
TreeNode node = list.removeFirst();
if (!array[i].equals("null")) {
node.left = new TreeNode(Integer.valueOf(array[i]));
list.addLast(node.left);
}
i++;
if (!array[i].equals("null")) {
node.right = new TreeNode(Integer.valueOf(array[i]));
list.addLast(node.right);
}
i++;
}
return root;
}
}
// Your Codec object will be instantiated and called as such:
// Codec ser = new Codec();
// Codec deser = new Codec();
// TreeNode ans = deser.deserialize(ser.serialize(root));
把二叉树转换为累加树
给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下，二叉搜索树满足下列约束条件：
节点的左子树仅包含键 小于 节点键的节点。
节点的右子树仅包含键 大于 节点键的节点。
左右子树也必须是二叉搜索树。
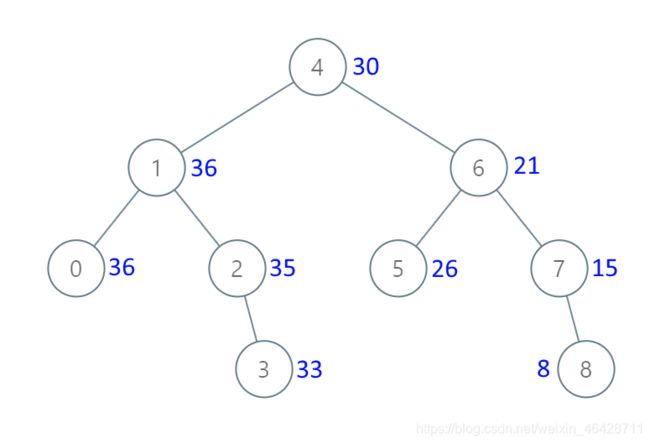输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2：
输入：root = [0,null,1]
输出：[1,null,1]
示例 3：
输入：root = [1,0,2]
输出：[3,3,2]
示例 4：
输入：root = [3,2,4,1]
输出：[7,9,4,10]
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/convert-bst-to-greater-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
思路
这题需要理解的是二叉搜索树的反向中序遍历（右，中，左）就是树的值从大到小的顺序。然后我们依次不断更新sum值和节点值即可。
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
int sum = 0;
public TreeNode convertBST(TreeNode root) {
if (root != null) {
convertBST(root.right);
sum += root.val;
root.val = sum;
convertBST(root.left);
}
return root;
}
}
二叉树的直径
给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
示例 :
给定二叉树
1
/ \
2 3
/ \
4 5
返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
注意：两结点之间的路径长度是以它们之间边的数目表示。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/diameter-of-binary-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
思路
这题其实就是求二叉树的深度的类似题目，我们要求一个节点的直径，其实就是求他左右子树的深度的和。我们只用定义一个变量用来记录当前遇到的最大值即可。
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
int max = 0;
public int diameterOfBinaryTree(TreeNode root) {
dfs(root);
return max;
}
public int dfs(TreeNode root) {
if (root == null) {
return 0;
}
int lefthigh = dfs(root.left);
int righthigh = dfs(root.right);
int sum = lefthigh + righthigh;
max = (max > sum) ? max : sum;
return Math.max(lefthigh,righthigh) + 1;
}
}
合并二叉树
给定两个二叉树，想象当你将它们中的一个覆盖到另一个上时，两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠，那么将他们的值相加作为节点合并后的新值，否则不为 NULL 的节点将直接作为新二叉树的节点。
示例 1:
注意: 合并必须从两个树的根节点开始。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/merge-two-binary-trees
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
思路
思路就是计算当前节点两个二叉树的和，如果一个为空那么直接返回另一个即可。
如果不为空那么就接着递归调用下面的节点。
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
if (root1 == null) {
return root2;
}
if (root2 == null) {
return root1;
}
TreeNode node = new TreeNode(root1.val + root2.val);
TreeNode lefttree = mergeTrees(root1.left, root2.left);
TreeNode righttree = mergeTrees(root1.right, root2.right);
node.left = lefttree;
node.right = righttree;
return node;
}
}
从前序与中序遍历序列构造二叉树
给定一棵树的前序遍历 preorder 与中序遍历 inorder。请构造二叉树并返回其根节点。
示例 1:
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
示例 2:
Input: preorder = [-1], inorder = [-1]
Output: [-1]
提示:
1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均无重复元素
inorder 均出现在 preorder
preorder 保证为二叉树的前序遍历序列
inorder 保证为二叉树的中序遍历序列
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
思路
这题的思路就是将中序遍历的结果和角标存放到hashmap中。然后我们开始前序遍历，遍历到的第一个节点其实就是根节点，然后我们就从中序遍历中找到这个节点，在这个节点的角标前的就是左子树，后的就是右子树。
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
HashMap<Integer, Integer> inmap = new HashMap<>();
int[] preorder;
public TreeNode buildTree(int[] preorder, int[] inorder) {
this.preorder = preorder;
for (int i = 0; i < inorder.length; i++) {
inmap.put(inorder[i], i);
}
return mybuildtree(0, 0, preorder.length - 1);
}
public TreeNode mybuildtree(int prerootindex, int inleft, int inright) {
if (inleft > inright) {
return null;
}
TreeNode root = new TreeNode(preorder[prerootindex]);
int inindex = inmap.get(root.val);
root.left = mybuildtree(prerootindex + 1, inleft, inindex - 1);
root.right = mybuildtree(prerootindex + 1 + inindex - inleft, inindex + 1, inright);
return root;
}
}
这里需要说明一下，在右子树传入的参数中第一个根节点之所以是prerootindex + 1 + inindex - inleft，是因为我们右子树的根节点就是初始根节点的位置 + 1(即左子树的根节点）然后加上左子树的长度（inindex - 1 - inleft + 1），所以最后我们得到的参数就变成上面这样了。
二叉树求权值最大，最小节点的路径
有一棵二叉树，树上每个点标有权值，权值各不相同，给定二叉树的根节点为root，请找出权值最大的节点与权值最小的节点; 假设父子节点距离为1，请计算权值最大节点与权值最小节点之间的距离
思路
这题是上次笔试遇到的，当时已经想到了求两个节点的最近公共祖先，可惜最后一步算距离没想到怎么算，现在总结下。
思路首先是找到这两个最大权值和最小权值的点。然后我们根据这两个点的值去找到他们的最近公共祖先。然后分别计算两个点到最近公共祖先的值，然后相加即可。
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
getMax(root);
getMin(root);
TreeNode lca = getlca(root, max, min);
int dis1 = getdis(lca, max);
int dis2 = getdis(lca, min);
return dis1 + dis2;
}
public void getMax(TreeNode root) {
if (root == null) {
return;
}
max = Math.max(max, root.val);
getMax(root.left);
getMax(root.right);
}
public void getMin(TreeNode root) {
if (root == null) {
return;
}
min = Math.min(min, root.val);
getMin(root.left);
getMin(root.right);
}
public TreeNode getlca(TreeNode root, int p, int q) {
if (root == null || root.val == p || root.val == q) {
return root;
}
TreeNode left = getlca(root.left, p, q);
TreeNode right = getlca(root.right, p, q);
if (left == null && right == null) {
return null;
}
if (left == null) {
return right;
}
if (right == null) {
return left;
}
return root;
}
public int getdis(TreeNode root, int nodeval) {
if (root == null) {
return -1;
}
if (root.val == nodeval) {
return 0;
}
int distance = getdis(root.left, nodeval);
if (distance == -1) {
distance = getdis(root.right, nodeval);
}
if (distance != -1) {
return distance + 1;
}
return -1;
}
}