112. 路径总和详解!!三种解法,总有一款适合你(Java)
513.找树左下角的值
题目链接:513. 找树左下角的值
BFS(迭代)法:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int findBottomLeftValue(TreeNode root) {
// 1. BFS法
int result = 0;
Queue queue = new ArrayDeque<>();
queue.add(root);
while(!queue.isEmpty()) {
int len = queue.size();
result = queue.peek().val; // 保存每一层的第一个元素(即对首元素)的值
// 开始层序遍历
while(len > 0) {
TreeNode temp = queue.poll();
if(temp.left != null) {
queue.add(temp.left);
}
if(temp.right != null) {
queue.add(temp.right);
}
len--;
}
}
return result;
}
} DFS(递归法)有点难,过段时间再补上吧
112. 路径总和
题目链接:112. 路径总和
DFS+哈希法:
这道题,和257. 二叉树的所有路径有点像,可以说是拓展题了,我也写过题解(点击跳转)。这道题,函数参数我设计的是每个节点上的值的集合List
代码:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
// DFS(前序遍历 + 哈希法)
if(root == null) {
return false;
}
Set pathValSumSet = new HashSet<>(); // 保存每一条路径上的和
List pathVal = new ArrayList<>(); // 保存路径上节点的值,因为要回溯,所以函数参数应该也有路径上值的集合
getAllPathSum(root, pathVal, pathValSumSet);
if(pathValSumSet.contains(targetSum)) { // 在哈希表中查找目标和是否存在二叉树所有路径和中
return true;
}else {
return false;
}
}
public void getAllPathSum(TreeNode node, List pathVal, Set pathValSumSet) {
pathVal.add(node.val);
if(node.left == null && node.right == null) { // 如果遇到叶子结点,说明要记录这条路径的和了
int sum = 0;
for(int i = 0; i < pathVal.size(); i++) { // 求路径总和
sum += pathVal.get(i);
}
// 把一跳路径上的和保存到pathValSumSet表中
pathValSumSet.add(sum);
return; // 循环终止条件就是到叶子节点就return就行了
}
if(node.left != null) { // 必须加上,因为可能出现有左孩子(右孩子)没有右孩子(左孩子),如示例1右下角边4这个结点,只有右孩子而没有左孩子,不加这句话会报空指针异常
getAllPathSum(node.left, pathVal, pathValSumSet);
// 出了上面这个函数,说明一定是走到叶子结点了,因为是前序遍历,已经经历了上一个函数对这条路径的求和
// 所以需要“回溯”,即把当前的pathVal集合里存放的最后一个元素(已经求过和的叶子结点的值)删除,这样再下一次往右孩子走时,计算的是另一条路径的和了
// 例如,走出上面的递归,此时pathVal里的元素是示例1里的[5, 4, 11, 7]
// 下面将会递归进入node.right(11这个结点的右孩子),此时如果不删除pathVal里的最后一个元素,那么进入求和则会导致结果出错
// 因为右孩子的路径总和应该是:[5, 4, 11, 2]
// 所以,以上便是回溯的原因!
pathVal.remove(pathVal.size() - 1);
}
if(node.right != null) {
getAllPathSum(node.right, pathVal, pathValSumSet);
pathVal.remove(pathVal.size() - 1);
}
}
} 本题用到了回溯,如下面这部分代码:
if(node.left != null) {
getAllPathSum(node.left, pathVal, pathValSumSet);
pathVal.remove(pathVal.size() - 1); // 回溯
}
回溯解读:
出了getAllPathSum(node.left, pathVal, pathValSumSet);这个函数,说明一定是走到叶子结点了,因为是前序遍历,已经经历了上一个函数对这条路径的求和所以需要“回溯”,所以接下来需要把当前的pathVal集合里存放的最后一个元素(已经求过和的叶子结点的值)删除,这样再下一次往右孩子走时,计算的是另一条路径的和了
例如,出了上面的getAllPathSum之后,此时pathVal里的元素是示例1里的[5, 4, 11, 7]
下面将会递归进入node.right(11这个结点的右孩子),此时如果不删除pathVal里的最后一个元素,那么进入求和则会导致结果出错
因为右孩子的路径总和应该是:[5, 4, 11, 2],所以,需要把pathVal里的最后一个元素删除(对应代码:pathVal.remove(pathVal.size() - 1);),这就叫:回溯!
DFS+Lst集合法:
当然,也可以不用哈希表,把递归的返回值和参数换一下,把哈希表直接换成targetSum,遇到对的的目标值一路返回true即可。
代码:
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
// DFS(前序遍历 )
if(root == null) {
return false;
}
List pathVal = new ArrayList<>(); // 保存路径上节点的值,因为要回溯,所以函数参数应该也有路径上值的集合
return getAllPathSum(root, pathVal, targetSum);
}
public boolean getAllPathSum(TreeNode node, List pathVal, int targetSum) {
pathVal.add(node.val);
if(node.left == null && node.right == null) { // 如果遇到叶子结点,说明要记录这条路径的和了
int sum = 0;
for(int i = 0; i < pathVal.size(); i++) { // 求路径总和
sum += pathVal.get(i);
}
if(sum == targetSum) {
return true;
}
}
if(node.left != null) {
if(getAllPathSum(node.left, pathVal, targetSum)) { // 如果找到了这条路径,那么就一直返回true即可
return true;
}else{
pathVal.remove(pathVal.size() - 1);
}
}
if(node.right != null) {
if(getAllPathSum(node.right, pathVal, targetSum)) {
return true;
}
else {
pathVal.remove(pathVal.size() - 1);
}
}
return false; // 走到这,一般是叶子节点,返回false,到时候会让它的父节点走到回溯的
}
} 但是当我看到提交之后只击败了15.14%的人!这可激发了我的好胜心!!!说明还能优化。
DFS法(纯享版):
仔细一想,这里也不需要用上LIst集合啊,这和257. 二叉树的所有路径不完全相同,那道题除了要打印值,还要打印一个"->"这个东东,所以用结合存储字符串好用来拼接,而且那道题也不是为了求和,关键是打印每一条路径,要体现各个节点的值,所以,最终重写了我的getAllPathSum方法,把方法参数改成只需要二叉树+目标和,也依然有回溯的影子,注意对比我这三个代码,总算对回溯有了一定滴认识啦。
代码:
class Solution {
int pathValSum = 0; // 保存某条路径上的和,放在外面是为了作为全局变量,可以累加和
public boolean hasPathSum(TreeNode root, int targetSum) {
// DFS(前序遍历 )
if(root == null) {
return false;
}
return getAllPathSum(root, targetSum);
}
public boolean getAllPathSum(TreeNode node, int targetSum) {
pathValSum += node.val;
if(node.left == null && node.right == null) { // 如果遇到叶子结点,判断目前这条路径上的和,是否等于目标值
if(pathValSum == targetSum) {
return true;
}/*
else{
pathValSum -= node.val;
} 这里不能这么写!!这样写并不是回溯!!,这样写的意思则表示遇到叶子节点不是目标值的才减叶子结点,
但是,我们的目的是一跳路径上的,这样减只减掉了叶子结点上的值,没有回溯
*/
}
if(node.left != null) {
if(getAllPathSum(node.left, targetSum)) { // 如果找到了这条路径,那么就一直返回true即可
return true;
}else {
pathValSum -= node.left.val; // 回溯!小子
}
}
if(node.right != null) {
if(getAllPathSum(node.right, targetSum)) {
return true;
}else {
pathValSum -= node.right.val;
}
}
return false;
}
}嘿嘿~这下舒服了。
从中序与后序遍历序列构造二叉树
题目链接:106. 从中序与后序遍历序列构造二叉树
看完视频讲解和题解还算清晰了,关键是找分割,看完题解和视频后自己写了一下代码,直接用数组手撕的,过是过了,只是......
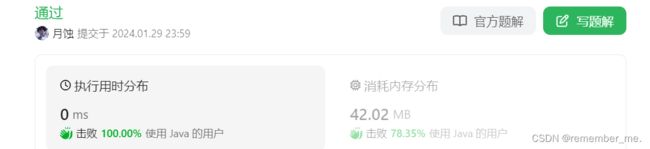
运行结果图:
这执行时间!这消耗内存,属实是有点拉胯了,emmm,代码如下。
自己敲的代码:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
if(postorder.length == 0) {
return null;
}
int nodeVal = postorder[postorder.length - 1]; // 后序最后一个元素即是根节点值
TreeNode node = new TreeNode(nodeVal);
if(postorder.length == 1) {
return node;
}
int delIndex = 0;
// 先在中序遍历中找分割节点
for(delIndex = 0; delIndex < inorder.length; delIndex++) {
if(inorder[delIndex] == nodeVal) {
break;
}
}
// 现在,在inorder中delIndex左边是左子树,右边是右子树
// 下面是保存前序左区间,与右区间
int[] inorderLeft = new int[delIndex]; // 注意大小,需要根据切割点来创建
int[] inorderRight = new int[inorder.length - delIndex - 1];
int inorderLeftSize = 0;
int inorderRightSize = 0;
for(int i = 0; i < delIndex; i++) {
inorderLeft[inorderLeftSize++] = inorder[i];
}
for(int i = delIndex + 1; i < inorder.length; i++) {
inorderRight[inorderRightSize++] = inorder[i];
}
// 根据中序的大小,来切割后序左右区间
int[] postorderLeft = new int[inorderLeftSize]; // 显然,后序遍历的左右区间大小和中序的左右区间大小是一样的,所以定义的时候直接用
int[] postorderRight = new int[inorderRightSize];
int postorderLeftSize = 0;
int postorderRightSize = 0;
for(int i = 0; i < inorderLeftSize; i++) {
postorderLeft[postorderLeftSize++] = postorder[i];
}
for(int i = inorderLeftSize; i < postorder.length - 1; i++) {
postorderRight[postorderRightSize++] = postorder[i];
}
node.left = buildTree(inorderLeft, postorderLeft); // 左子树,用中序的左区间+后序的左区间
node.right = buildTree(inorderRight,postorderRight);
return node;
}
}显然,有很多累赘的,或者说,很多代码复用性不强,像每次分割左右区间的时候,都会定义各自区间的大小,关键原因就在于,设计这个递归函数的时候,我就是直接用题目给的函数进行递归的,能过是能过,但是。。。。上面的运行时长就是结果。当然,这里可以优化的,也就是卡哥代码里给的,分割区间的时候,关键就在于:
1. 根据后序最后一个元素,在中序遍历中去“找”到这个这个元素对应位置,然后展开下面的分割。
2. 其实这些元素全部都在inorder数组和postorder数组中,只需要拿到了每个区间的始末,然后逐渐分割,利用后序遍历的最后一个元素就是节点的规则(new TreeNode的位置),去创建节点就是。
对应第一点,“找”,可以利用哈希法来找,因为哈希法最擅长“找”这个操作了,显然,这里需要根据值找到下标,所以用map。然后第二点,便是把我上面代码中创建数组和分割数组,改成只通过下标来更改递归即可。根据上面这两点,可以写出下面的优化代码(直接拿代码随想录里的了):
优化代码:
class Solution {
Map map; // 方便根据数值查找位置
public TreeNode buildTree(int[] inorder, int[] postorder) {
map = new HashMap<>();
for (int i = 0; i < inorder.length; i++) { // 用map保存中序序列的数值对应位置
map.put(inorder[i], i);
}
return findNode(inorder, 0, inorder.length, postorder,0, postorder.length); // 前闭后开
}
public TreeNode findNode(int[] inorder, int inBegin, int inEnd, int[] postorder, int postBegin, int postEnd) {
// 参数里的范围都是前闭后开
if (inBegin >= inEnd || postBegin >= postEnd) { // 不满足左闭右开,说明没有元素,返回空树
return null;
}
int rootIndex = map.get(postorder[postEnd - 1]); // 找到后序遍历的最后一个元素在中序遍历中的位置
TreeNode root = new TreeNode(inorder[rootIndex]); // 构造结点
int lenOfLeft = rootIndex - inBegin; // 保存中序左子树个数,用来确定后序数列的个数
root.left = findNode(inorder, inBegin, rootIndex,
postorder, postBegin, postBegin + lenOfLeft);
root.right = findNode(inorder, rootIndex + 1, inEnd,
postorder, postBegin + lenOfLeft, postEnd - 1);
return root;
}
}