就你小子叫回溯（su）是吧！

今天第一次来系统性学回溯算法，下面将结合代码随想录和力扣上的例题来更深一步了解回溯算法。

理解回溯：

回溯呢，听名字，关键在“回”一字，而正所谓：“有来有回。”，没有“来”，哪来“回”一说，所以，“回”之前，必须要有“来”，这里的“来”，就是我们熟悉的“递归”，即：

出现回溯之前，必定是递归的调用。

文字上的解释向来都不是深刻的解释，唯有通过例题，才能让我们更加深刻的理解，所以，下面将介绍会用到“回溯法”的经典例题，通过了解这些例题的做法，我们也能更加深刻的理解回溯法！ 

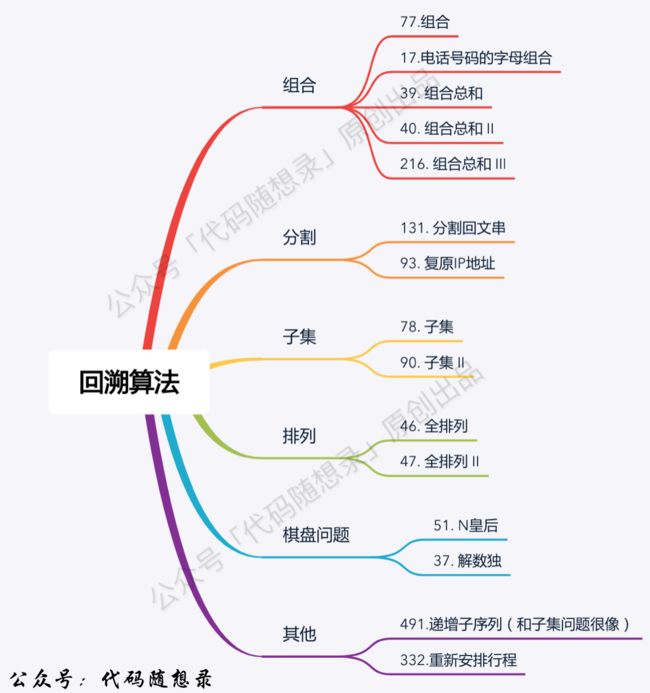
回溯法经典例题：

 （以上的内容，代码随想录中有更详细的解释，这里我只介绍一下“我所理解的回溯”，卡哥大佬写的文章也讲的很详细了，文章链接：代码随想录 (programmercarl.com)）

下面，将通过一道简单的例题，来更加深刻的理解回溯法！

77. 组合

题目链接：77. 组合

这是一道力扣上的经典例题，这道题乍一看，用循环枚举也能做啊，嘿嘿，那是题目给的两个示例可以这么干，比如第一个示例，只需要求1-4中的两个数字组成的组合，两层for循环就轻松搞定了，但是！别忘了题目中要求的是“n个数中，k个数的组合”，如果k是50呢？50个for循环？而且k也是不确定的啊，所以，这道题，简单的列举for循环枚举是不行滴。而还想通过枚举的方式去做，就只有我们今天的主角：回溯法才能解决了。

思路：

那示例1来举例，按照正常的思路是：先取一个1，存入一个临时集合temp中，然后再在剩下的234中再取1个2，存入temp中，这时判断到，已经有两个数了，满足组合条件，把这个临时的temp存入到结果集result中去，而下面的操作，应该是丢掉2，把3加入到temp中，在result中存入temp，求掉3，把4加入到temp中，在result中存入temp，然后，再把temp中两个元素再清空，重复上面的步骤。

上面这一通操作，是不是很像递归啊，没错，这道题，就是递归，哎，那回溯，藏在哪呢？仔细观察，就在上面思路中“丢掉x”，这一步，就是我们的回溯。仔细观察，发现，“丢掉x”的这一步思想，往往就是在这一层递归结束之后，要下一次递归之前，进行的回溯。而这一现象，在题解的代码中，也可以体现！下面是上代码时间！

代码1.0：

class Solution {
    List temp = new ArrayList<>();
    List> result = new ArrayList<>(); // 定义两个全局变量，用于存储结果
    public List> combine(int n, int k) {
        backtracking(n, k, 1); // 调用递归函数
        return result;
    }
    // 1. 函数返回值与参数，需要设置一个起始点下标，来控制每一次递归时搜索的起点，可以确保每一次搜索元素不重复
    public void backtracking(int n, int k, int startIndex) {
        // 2. 终止条件
        if(temp.size() == k) {
            result.add(new ArrayList<>(temp)); // new的这一步很关键！result中存放的是不同的集合！不是一个集合，通过new才能创建一个新的集合空间！！
            return;
        }
        // 3. 单层递归逻辑
        for(int i = startIndex; i <= n; i++) {
            temp.add(i);
            backtracking(n, k, i + 1); // 递归
            temp.remove(temp.size() - 1);// 回溯，确保下一次递归时，temp中保留部分元素
        } 

    }
}

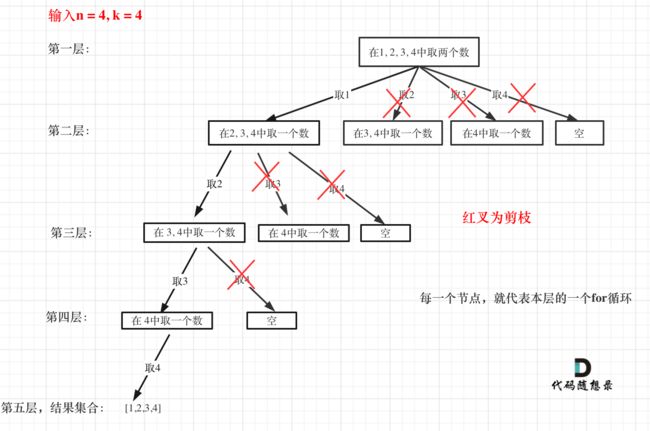
而所有的回溯法，都可以用树形图来辅助理解，下面是代码随想录中的图，借用一下：

代码2.0：

然而！上面我给的是代码1.0，莫非还有优化？没错，是可以优化的，回溯法，本质还是一种暴力枚举，算法的效率并不是特别高，所以可以通过“剪枝”（就是把明显不可能的情况，不再进入递归（循环），从而减少递归（循环）的次数）的方式来优化。 显而易见的一个例子是，当n=4，k=4时，显然，当i=2之后的所有，都不满足，而且，在进入i=1之后，也只有1234这一中情况，如下图：

而什么情况时，我们需要剪枝呢？首先我们应该知道下面几个变量：

n - i ：每一层循环中，加入这个 i 之后，集合中还能取到的元素数目。例如，当i = 2，n = 5，n - i = 3，3(n-i) 表示当加入2后，接下来的集合中，还能取得的元素数目。

temp.size()：当前这一层循环中，已有的元素，如上图中第二层的temp.size()=1，表示第二层此时只有一个元素。

k - temp.size()：表示接下来还需要加入k - temp.size()个数才能达到“组合”所要求的个数。

显然，只有当n - i 不小于 k - temp.size()时，才需要进行下面的递归，因为，当集合中还能取到的元素数目都小于还需要加入的k - temp.size()个数时，那么下面的递归就没有意义了，直接排除不进入，这就是剪枝。代码如下：

class Solution {
    List temp = new ArrayList<>();
    List> result = new ArrayList<>(); // 定义两个全局变量，用于存储结果
    public List> combine(int n, int k) {
        backtracking(n, k, 1); // 调用递归函数
        return result;
    }
    // 1. 函数返回值与参数，需要设置一个起始点下标，来控制每一次递归时搜索的起点，可以确保每一次搜索元素不重复
    public void backtracking(int n, int k, int startIndex) {
        // 2. 终止条件
        if(temp.size() == k) {
            result.add(new ArrayList<>(temp)); // new的这一步很关键！result中存放的是不同的集合！不是一个集合，通过new才能创建一个新的集合空间！！
            return;
        }
        // 3. 单层递归逻辑
        for(int i = startIndex; i <= n; i++) {
            temp.add(i);
            // 剪枝操作：
            if(!(n - i < k - temp.size())){
                // n - i 表示的是加入这个数字后，还剩下的数字
                // k - temp.size()表示，还需要的元素
                // 显然，只有当剩下的元素，不小于还需要的元素时，才能完成组合，才需要继续往下一层递归
                
                backtracking(n, k, i + 1);
            }// 如果这个if不满足，那么没必要进入下一层递归，直接把刚刚加入的元素删除即可
            
            temp.remove(temp.size() - 1);// 回溯，确保下一次递归时，temp中保留部分元素
        } 

    }
}

 

怎么样，这样一看，代码似乎并不难，回溯也就这样？而且有个好消息，回溯法，是有模板的！有模板的东西，就会清晰很多啦。

回溯法代码模板：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

通过模板，我们也可以看到，回溯法的递归函数，往往返回值是void哦。

 总结：

不管是不剪枝的代码，还是剪枝的代码，核心代码，其实就是递归和回溯的部分，其实回溯也是因为，在取得下一个新的数字时，并不需要完全用到之前的元素所以，在找到了一个满足条件的组合之后，删除这个满足条件的组合中的一个元素，然后返回到上一层递归中，接着下一次循环...这样的过程，就是回溯。

关于性能的拓展：

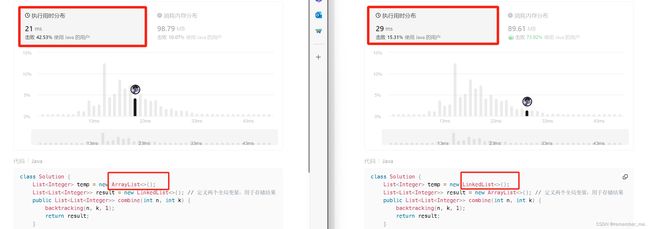
在上面的代码中，List集合的实例化，是有两种类可以选择的，分别是：LinkedList和ArrayList。而在一般的理解中：

经常要用到插入和删除会用：LinkedList

而经常会用到访问则用：ArrayList

 为什么？因为LinkedList底层实现是链表，链表的插入和删除是方便很多的，只需要O(1)的时间复杂度，而ArrayList底层实现是数组，数组的插入和删除，我们知道，是需要O(n)的，这道题中，temp的实例，我们用的还是ArrayList啊，在回溯中，明显要经常用到删除啊，为什么还用ArrayList啊？嘿嘿，对于这个，应该对底层实现更深刻一点，LinkedList的插入和删除比ArrayList快，是快在中间和头部的插入和删除，在结尾的删除，数组还不一定比链表慢，相反应该会更快！因为链表访问到最后一个元素，时间复杂度是O(n)哦，链表需要一步步移动到最后一个，再来O(1)的复杂度来删除，而数组，可以直接用O(1)的复杂度到达最后一个元素，然后也用O(1)复杂度删除，这样分析，数组是更快的哦。所以，何时用LinkedList，何时用ArrayList，应该是下面的总结：

经常要用到中间或者开头的插入和删除会用：LinkedList

而经常会用到访问则用：ArrayList

（如果经常直在结尾删除，也可用ArrayList）

 下面是关于这道题，temp用LinkedList或ArrayList实例化后代码1.0AC的性能差异图对比：

 这也算是一个小小的体外话，今天的文章更重要的是对回溯的理解，更多详细的内容在这题的代码随想录中有，文章链接：代码随想录 (programmercarl.com)