动态规划——判断子序列
"Don’t watch the clock; do what it does. Keep going."
- Sam Levenson
1. 题目描述
2. 题目分析与解析
上一篇文章讲解了如何使用双指针与使用一个二维数组来解决,这篇文章我们看一看动态规划来解决该问题。
我们在拿到一个问题时,如何知道能不能用动态规划解决呢?总不可能看见一个问题就把动态规划往上套,所以接下来我们先讨论这个问题。
动态规划(Dynamic Programming, DP)是一种用于解决具有重叠子问题和最优子结构性质的问题的算法技术。它通过将原问题分解为更小的子问题,解决每个子问题只一次,并存储它们的解,在需要时再次利用,以此减少计算量。
通过上述的描述我们可以看出动态规划主要用于解决具有重叠子问题和最优子结构性质的问题,而解决的核心就是:将原问题分解为更小的子问题,解决每个子问题只一次,并存储它们的解。因此如何判断能否使用动态规划?那就根据提到的需要识别该问题是否具有以下两个主要特征:
-
重叠子问题 (Overlapping Subproblems)
问题的解决方案需要重复解决相同的子问题而不是总是生成新的子问题。例如,在计算斐波那契数列的值时,要得到fib(n),你需要计算fib(n-1)和fib(n-2),而这两个值又都依赖于更小的斐波那契数。在没有优化的情况下,许多子问题会被重复计算多次,这就是重叠子问题的典型场景。
-
最优子结构 (Optimal Substructure)
一个问题的最优解包含了其子问题的最优解。换句话说,问题的总最优解可以通过组合其子问题的最优解来得到。例如,在最长公共子序列(LCS)问题中,两个序列的LCS长度可以通过考查两个序列的前缀的LCS长度来确定。
-
判断步骤
-
识别问题类型:首先识别问题是否属于已知的可以用DP解决的问题类型,如上文所述的问题列表。
-
寻找重叠子问题:尝试分解问题,看是否存在可以重复解决的子问题。如果你发现问题可以被分解成更小的子问题,并且这些子问题之间有重复,那么这是使用DP的一个信号。
-
检查最优子结构:检查问题是否可以通过子问题的最优解组合来解决。你可以通过分析问题是否允许你将大问题分解为小问题,并且通过解决小问题的方式来构建整个问题的解决方案,来确定问题是否具有最优子结构。
-
考虑状态定义:思考如何定义问题的状态,以及如何通过较小的状态来表达较大的状态。状态通常表示为问题的某个参数或参数的组合,其解决方案可以用来构建更大问题的解决方案。
-
构思状态转移方程:最后,尝试构建状态转移方程,即如何从一个或多个较小的状态推导出当前状态的解。状态转移方程是DP解决方案的核心,它定义了如何通过子问题的解来达到当前问题的解。
现在回到我们的题目,首先判断该题目是否能使用动态规划解决。
2.1 识别问题类型
-
判断一:是否存在重叠子问题
是:因为每一个s字符x需要再 t 字符串中寻找,而s当前字符的下一个字符y肯定是在 t 中尽量找离当前字符x最近的字符y,也就是我对每一个s字符串中的字符x进行判断其在t字符串中是否存在时,都是重复相同的步骤:找当前字符x是否存在,找离当前字符最近的下一个字符y
-
判断二:是否可以通过子问题的最优解组合来解决
否:因为不存在寻找最优解的问题
2.2 考虑状态定义
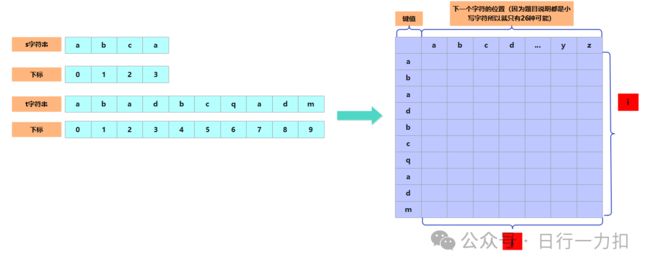
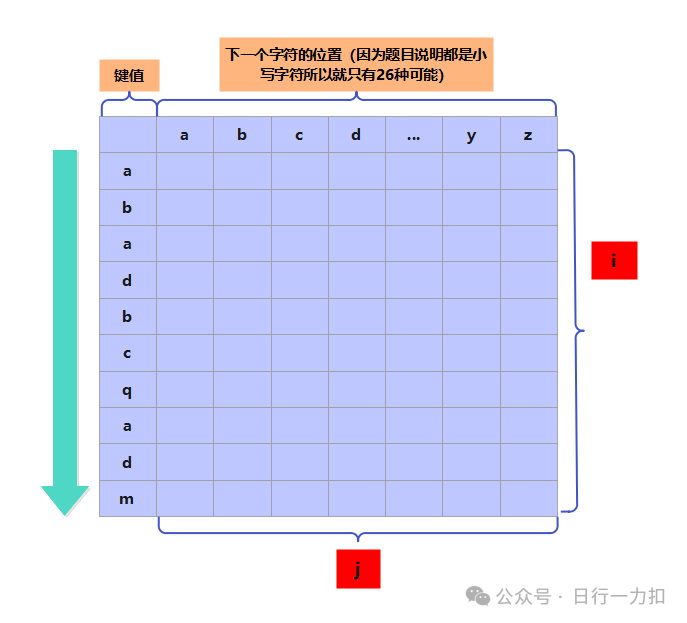
假设我现在需要找的字符 x 的下标为 i , 我就可以用一个二维数组 dp,行为 i ,表示t字符串的第i个字符,列为 j ,j 表示离当前字符 x 最近的下一个字符 y 的下标。
状态:dp[i][j]表示 t 字符串的第i个字符到 j 代表的下一个离得最近的字符 的位置
因为如果我们有了完整的状态转移表也就是dp数组,在后续搜寻s是否为t的子序列时,只需要根据状态转移数组dp,查看s每一个字符x的下一个字符y到的位置,如果能走到最后就说明是子序列,如果不行(也就是遇到了无穷大),则返回false。
所以现在的目标就是先把这个dp数组填写好,而状态转移方程就是填写该数组的最好最高效的方法。
2.3 构思状态转移方程
因为一般而言,状态转移方程的目的就是通过避免重复计算相同子问题的解,状态转移方程允许算法复用之前计算的结果,从而大大减少了计算的总量。所以我们就要从哪些值能最快算出来并且在之后能最高效的利用作为切入点。
可以看一下如果我们从前向后计算,如下箭头方向:
这种顺序带来的结果是每一行的值都需要重新向后遍历寻找当前字符的下一个字符的位置。
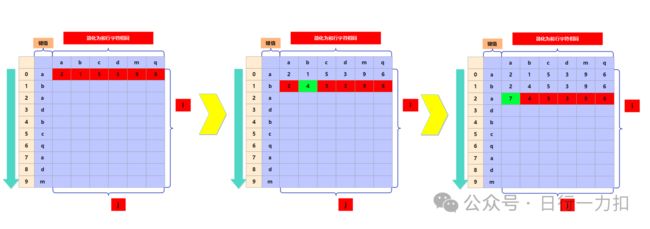
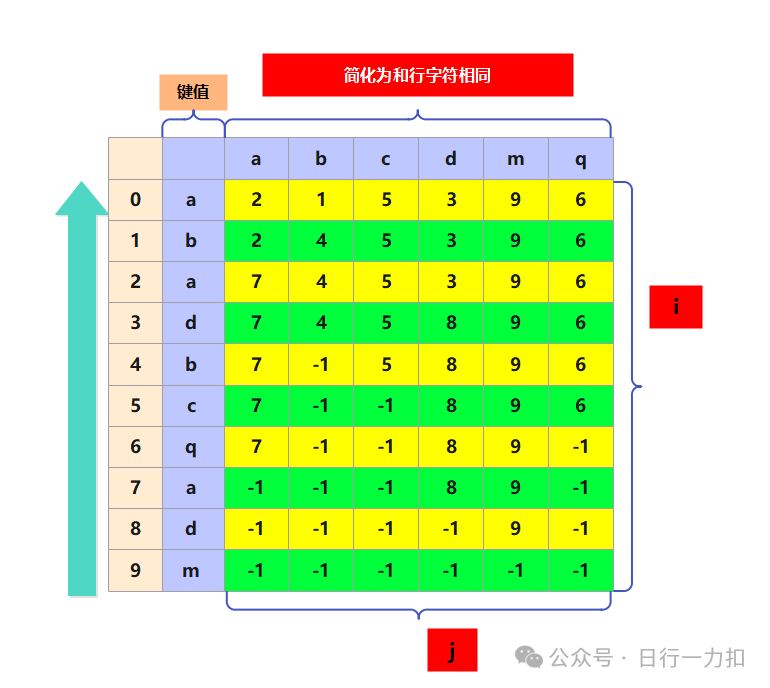
比如我们模拟一下,为了简化dp数组方便画图,我就先把dp数组的列设置为和行相同的字符(实际情况下也可以这样做,但是由于我需要遍历很多很多个s字符串,设置为26个最方便,不需要去多次改bp数组)如下:
首先我填写了第一行的bp数组值,但是我在填写第二行的时候,需要变更绿色的部分的值,也就是对于 b 字符处也就是dp[1][1]还需要向后去遍历再找一次。同理当遍历到第三行 a ,还需要向后找 a 的位置,也就是每一次到新的一行虽然能用到之前一部分的值,但是之前的字符的位置是需要变更的,增加了遍历的时间开销,这说明我们并没有找到合适的开始方向。
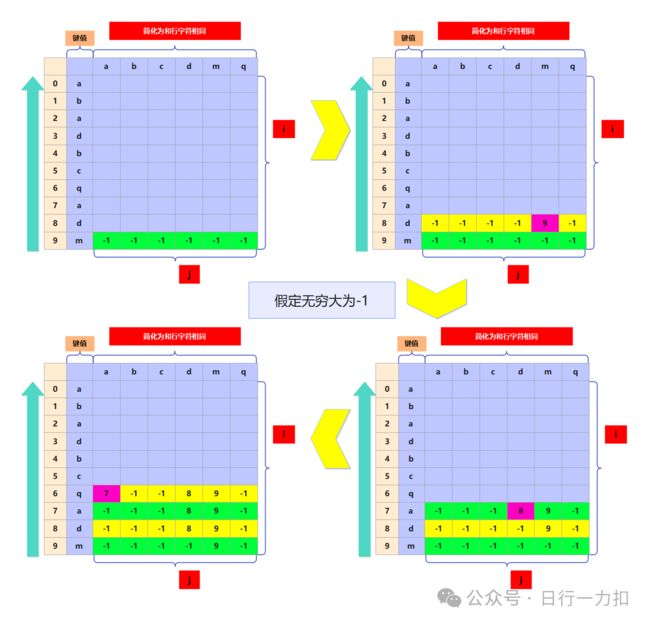
因此我们尝试换一个方向,从最后一个字符向前遍历,看看效果如何:
根据上图我觉得大多数人都能发现其奥妙:如果我从后向前遍历,那么我并不需要在计算每一行的值时再去寻找其它值,在每一次的变更的紫色框 中,大家应该都看出来了只需要更新与当前字符的下一个字符相同的列,并且更新的值就是下一个字符的下标。
因此我们就可以确定其状态转移方程了,从后向前:(注意最后一行特殊初始化为无穷大)
所以我们的基本结构就是根据上述构建bp数组,而后遍历s字符串,根据bp数组的序号一个一个去找。最终对于示例中的字符串t构建的bp数组如下:
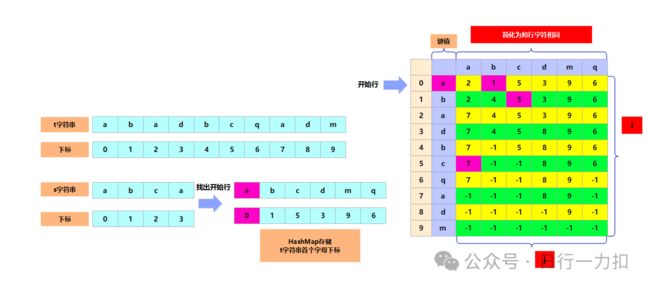
同时我们需要注意,因为我们设置的bp数组是横纵坐标其实都是数字,那么对于s中的第一个字符,我们是很难找到其对应的bp数组开始的行的。因此我们就需要使用一个hashMap,将t字符串中每一个首次出现的字符的位置存储起来,这样就能快速找到开始的行的位置。接下来用一个示例演示一下:
假设我们现在想找 s 字符串 abca 是否是 t 的子序列,那么我们的步骤就如下图所示:
能够走完全程所以,返回true。
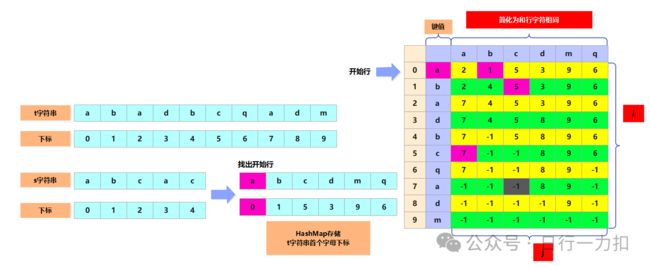
如果我想找的 s 字符串为 abcac 是否是 t 的子序列,那么我们的步骤就如下:
发现需要从a 找到 c,但是a到c 的位置为 -1,所以就停止,返回false。
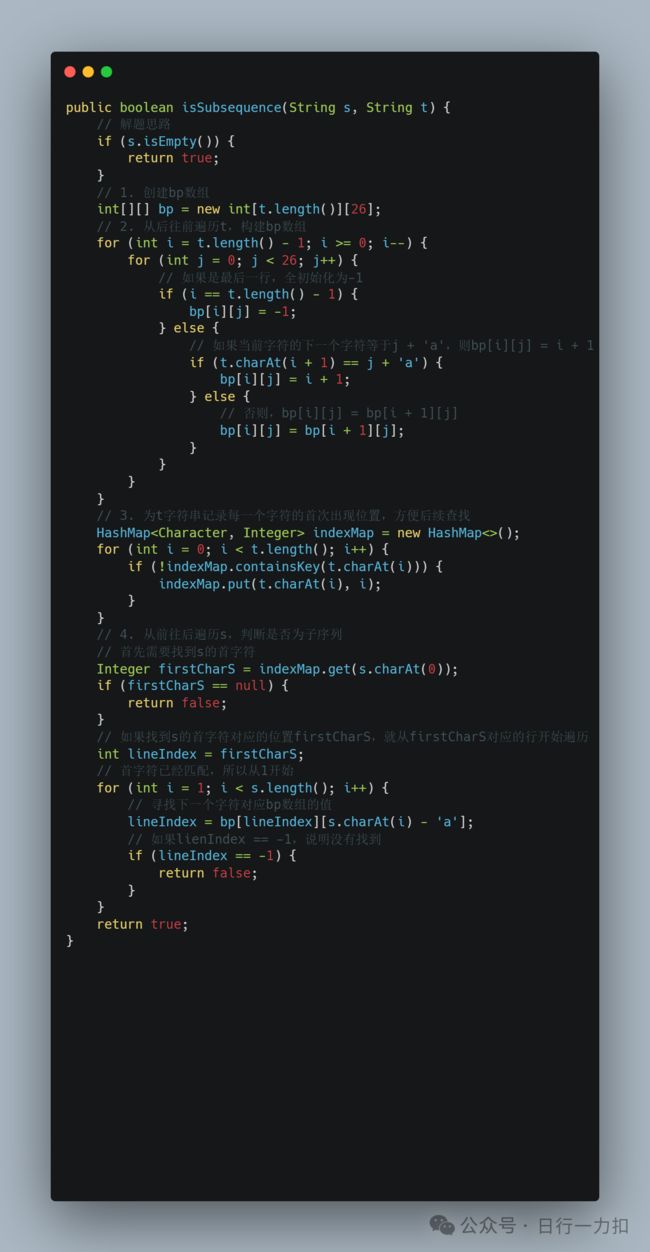
根据dp数组来判断是否是子序列问题,就只需要遍历一次短字符串 s ,明显降低了开销。根据上面的图解我想大家都能够自己编程实现动态规划来解决改题目了!