肯尼斯·里科《C和指针》第12章 使用结构和指针（1）链表

只恨当时学的时候没有读到这本书，，，，，，

12.1 链表

有些读者可能还不熟悉链表，这里对它作一简单介绍。链表(linked list)就一些包含数据的独立数据结构（通常称为节点）的集合。链表中的每个节点通过链或指针连接在一起。程序通过指针访问链表中的节点。通常节点是动态分配的，但有时也能看到由节点数组构建的链表。即使在这种情况下，程序也是通过指针来遍历链表的。

12.2 单链表

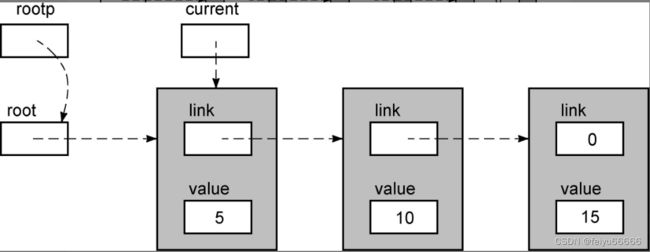
在单链表中，每个节点包含一个指向链表下一节点的指针。链表最后一个节点的指针字段的值为NULL，提示链表后面不再有其他节点。在找到链表的第1个节点后，指针就可以带你访问剩余的所有节点。为了记住链表的起始位置，可以使用一个根指针(root pointer)。根指针指向链表的第1个节点。注意，根指针只是一个指针，它不包含任何数据。

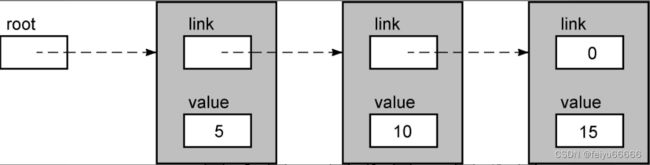
下面是一张单链表的图。

本例中的节点是用下面的声明创建的结构。

typedef struct  NODE   {
          struct  NODE   *link;
          int              value;
} Node;

存储于每个节点的数据是一个整型值。这个链表包含3个节点。如果从根指针开始，随着指针到达第1个节点，可以访问存储于那个节点的数据。随着第1个节点的指针可以到达第2个节点，可以访问存储在那里的数据。最后，第2个节点的指针带你来到最后一个节点。零值提示它是一个NULL指针，在这里它表示链表中不再有更多的节点。

在上面的图中，这些节点相邻在一起，这是为了显示链表所提供的逻辑顺序。事实上，链表中的节点可能分布于内存中的各个地方。对于一个处理链表的程序而言，各节点在物理上是否相邻并没有什么区别，因为程序始终用链（指针）从一个节点移动到另一个节点。

单链表可以通过链从开始位置遍历链表直到结束位置，但链表无法从相反的方向进行遍历。换句话说，当程序到达链表的最后一个节点时，如果想回到其他任何节点，就只能从根指针从头开始。当然，程序在移动到下一个节点前可以保存一个指向当前位置的指针，甚至可以保存指向前面几个位置的指针。但是，链表是动态分配的，可能增长到几百或几千个节点，所以要保存所有指向前面位置的节点的指针是不可行的。

在这个特定的链表中，节点根据数据的值按升序链接在一起。对于有些应用程序而言，这种顺序非常重要，比如根据一天的时间安排约会。对于那些不要求排序的应用程序，当然也可以创建无序的链表。

12.2.1 在单链表中插入

怎么才能把一个新节点插入到一个有序的单链表中呢？

假定我们有一个新值，比如12，想把它插入到前面那个链表中。从概念上说，这个任务非常简单：从链表的起始位置开始，跟随指针直到找到第一个值大于12的节点，然后把这个新值插入到那个节点之前的位置。

实际的算法则比较有趣。我们按顺序访问链表，当到达内容为15的节点（第一个值大于12的节点）时就停下来。我们知道这个新值应该添加到这个节点之前，但前一个节点的指针字段必须进行修改以实现这个插入。由于我们已经越过了这个节点，所以无法返回去。解决这个问题的方法就是始终保存一个指向链表当前节点之前的那个节点的指针。

我们现在将开发一个函数，把一个节点插入到一个有序的单链表中。程序12.1是我们的第一次尝试。

/*
** 插入到一个有序的单链表。函数的参数是一个指向链表第一个节点的指针以及需要插入的值。
*/
#include 
#include 
#include "sll_node.h"
#define    FALSE     0
#define    TRUE      1
int
sll_insert( Node *current, int new_value )
{
Node   *previous;
Node   *new;
/*
** 寻找正确的插入位置，方法是按顺序访问链表，直到到达其值大于或等于
** 新插入值的节点。
*/
while( current->value < new_value ){
      previous = current;
      current = current->link;
}
/*
** 为新节点分配内存，并把新值存储到新节点中，如果内存分配失败，
**  函数返回FALSE。
*/
new = (Node *)malloc( sizeof( Node ) );
if( new == NULL )
      return FALSE;
new->value = new_value;
/*
** 把新节点插入到链表中，并返回TRUE。
*/
new->link = current;
previous->link = new;
return TRUE;
}

程序12.1 插入到一个有序的单链表：第1次尝试insert1.c

用下面这种方法调用这个函数：

result = sll_insert(root,12);

让我们仔细跟踪代码的执行过程，看看它是否把新值12正确地插入到链表中。首先，传递给函数的参数是root变量的值，它是指向链表第一个节点的指针。当函数刚开始执行时，链表的状态如下。

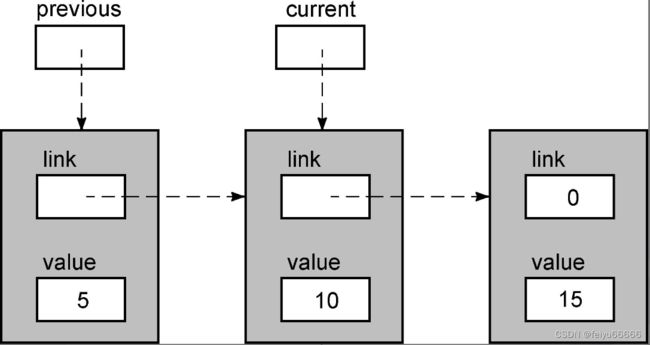
上图并没有显示root变量，因为函数不能访问它。它的值的一份副本作为形参current传递给函数，但函数不能访问root。现在current->value是5，它小于12，所以循环体再次执行。当回到循环的顶部时，current和previous指针都向前移动了一个节点。

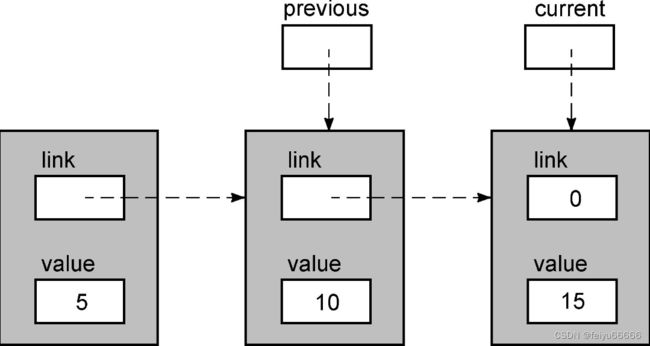
现在，current->value的值为10，因此循环体还将继续执行，结果如下。

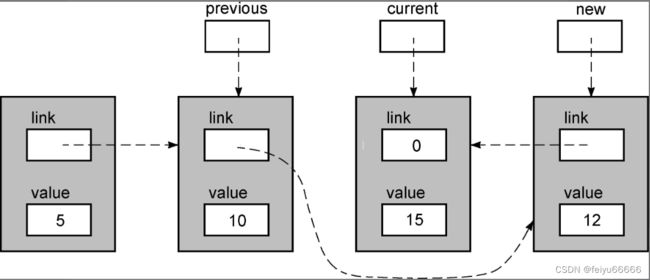
现在，current->value的值大于12，所以退出循环。

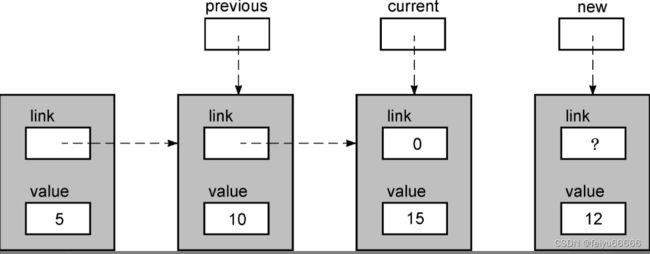
此时，重要的是previous指针，因为它指向我们必须加以修改以插入新值的那个节点。但首先，我们必须得到一个新节点，用于容纳新值。下面这张图显示了新值被复制到新节点之后链表的状态。

把这个新节点链接到链表中需要两个步骤。第一个步骤是执行下述语句：

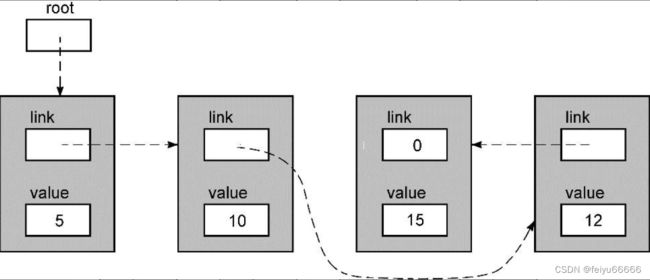
new->link = current;

使新节点指向将成为链表下一个节点的节点，也就是我们所找到的第一个值大于12的那个节点。在这个步骤之后，链表的内容如下所示。

第二个步骤是让previous指针所指向的节点（也就是最后一个值小于12的那个节点）指向这个新节点。下面这条语句用于执行这项任务：

previous->link = new;

这个步骤之后，链表的状态如下。

然后函数返回，链表的最终样子如下所示。

从根指针开始，随各个节点的link字段逐个访问链表，可以发现这个新节点已被正确地插入到链表中。

问题

不幸的是，这个插入函数是不正确的。试试把20这个值插入到链表中，你就会发现一个问题：while循环越过链表的尾部，并对一个NULL指针执行间接访问操作。为了解决这个问题，必须对current的值进行测试，在执行表达式current->value之前确保它不是一个NULL指针：

while( current != NULL & current->value < value ){

下一个问题更加棘手，试试把3这个值插入到链表中，看看会发生什么？

为了在链表的起始位置插入一个节点，函数必须修改根指针。但是，函数不能访问变量root。修正这个问题最容易的方法是把root声明为全局变量，这样插入函数就能修改它。不幸的是，这是最坏的一种解决方法。因为这样一来，函数只对这个链表起作用。

稍好的解决方法是把一个指向root的指针作为参数传递给函数。然后，使用间接访问，函数不仅可以获得root（指向链表第一个节点的指针，也就是根指针）的值，也可以向它存储一个新的指针值。这个参数的类型是什么呢？root是一个指向Node的指针，所以参数的类型应该是Node **，也就是一个指向Node的指针的指针。程序12.2的函数包含了这些修改。现在，我们必须以下面这种方式调用这个函数：

result = sll_insert( &root, 12 );
/*
** 插入到一个有序单链表。函数的参数是一个指向链表根指针的指针，以及一个需要插入的新值。
*/
#include 
#include 
#include "sll_node.h"
#define   FALSE    0
#define   TRUE        1
int
sll_insert( Node **rootp, int new_value )
{
       Node  *current;
       Node  *previous;
       Node  *new;
       /*
       ** 得到指向第1个节点的指针。
       */
       current = *rootp;
       previous = NULL;
       /*
       ** 寻找正确的插入位置，方法是按序访问链表，直到到达一个其值大于或等于
       ** 新值的节点。
       */
       while( current != NULL && current->value < new_value ){
             previous = current;
           current = current->link;
       }
       /*
       ** 为新节点分配内存，并把新值存储到新节点中，如果内存分配失败，
       **  函数返回FALSE。
       */
       new = (Node *)malloc( sizeof( Node ) );
       if( new == NULL )
           return FALSE;
       new->value = new_value;
       /*
       ** 把新节点插入到链表中，并返回TRUE。
       */
       new->link = current;
       if( previous == NULL )
           *rootp = new;
       else
           previous->link = new;
       return TRUE;
}

程序12.2 插入到一个有序单链表：第2次尝试insert2.c

这第2个版本包含了另外一些语句。

previous = NULL；

我们需要这条语句，这样以后就可以检查新值是否应为链表的第一个节点。

current = *rootp;

这条语句对根指针参数执行间接访问操作，得到的结果是root的值，也就是指向链表第一个节点的指针。

If (previous == NULL)
          *rootp = new;
else
          previous->link = new;

上述语句被添加到函数的最后，用于检查新值是否应该被添加到链表的起始位置。如果是，则使用间接访问修改根指针，使它指向新节点。

这个函数可以正确完成任务，而且在许多语言中，这是你能够获得的最佳方案。但是，我们还可以做得更好一些，因为C允许我们获得现存对象的地址（即指向该对象的指针）。

优化插入函数

看上去，把一个节点插入到链表的起始位置必须作为一种特殊情况进行处理。毕竟，我们此时插入新节点需要修改的指针是根指针。对于任何其他节点，对指针进行修改时实际修改的是前一个节点的link字段。这两个看上去不同的操作实际上是一样的。

消除特殊情况的关键在于：我们必须认识到，链表中的每个节点都有一个指向它的指针。对于第一个节点，这个指针是根指针；对于其他节点，这个指针是前一个节点的link字段。重点在于每个节点都有一个指针指向它。至于该指针是不是位于一个节点的内部则无关紧要。

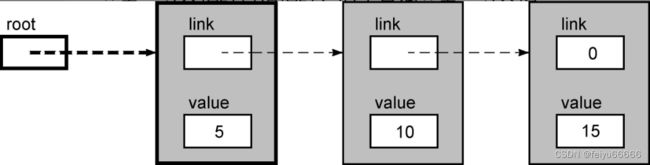
让我们再次观察这个链表，弄清这个概念。下面是第1个节点和指向它的指针。

如果新值插入到第1个节点之前，这个指针就必须进行修改。

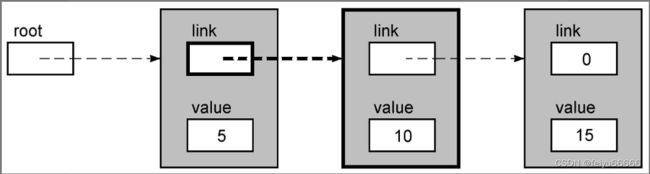
下面是第2个节点和指向它的指针。

如果新值需要插入到第2个节点之前，那么这个指针必须进行修改。注意，我们只考虑指向这个节点的指针，至于哪个节点包含这个指针则无关紧要。对于链表中的其他节点，都可以应用这个模式。

现在让我们看一下修改后的函数（当它开始执行时）。下面显示了第一条赋值语句之后各个变量的情况。

我们拥有一个指向当前节点的指针，以及一个“指向当前节点的link字段的”指针。除此之外，就不需要别的了！如果当前节点的值大于新值，那么rootp指针就会告诉我们哪个link字段必须进行修改，以便让新节点链接到链表中。如果在链表其他位置的插入也可以用同样的方式进行表示，就不存在前面提到的特殊情况了。关键在于我们前面看到的指针/节点关系。

当移动到下一个节点时，我们保存一个“指向下一个节点的link字段”的指针，而不是保存一个指向前一个节点的指针。我们很容易画出一张描述这种情况的图。

注意，这里rootp并不指向节点本身，而是指向节点内部的link字段。这是简化插入函数的关键所在，但我们必须能够取得当前节点的link字段的地址。在C中，这种操作是非常容易的。表达式¤t->link就可以达到这个目的。程序12.3是插入函数的最终版本。rootp参数现在称为linkp，因为它现在指向的是不同的link字段，而不仅仅是根指针。我们不再需要previous指针，因为link指针可以负责寻找需要修改的link字段。前面那个函数最后部分用于处理特殊情况的代码也不见了，因为我们始终拥有一个指向需要修改的link字段的指针——我们用一种和修改节点的link字段完全一样的方式修改root变量。最后，我们在函数的指针变量中增加了register声明，用于提高结果代码的效率。

我们在最终版本中的while循环中增加了一个窍门，它嵌入了对current的赋值。下面是一个功能相同但长度稍长的循环。

/*
** Look for the right place.
*/
current = *linkp;
while( current !=NULL && current->value < value ){
          linkp = ¤t->link;
current = * linkp;
}

一开始，current被设置为指向链表的第一个节点。while循环测试我们是否到达了链表的尾部。如果是，它接着检查我们是否到达了正确的插入位置。如果不是，循环体继续执行，并把linkp设置为指向当前节点的link字段，并使current指向下一个节点。

循环的最后一条语句和循环之前的那条语句相同，这就促使我们对它进行“简化”，方法是把current的赋值嵌入到while表达式中。其结果是一个稍为复杂但更加紧凑的循环，因为我们消除了current的冗余赋值。

/*
** 插入到一个有序单链表。函数的参数是一个指向链表第一个节点的指针，以及一个需要插入的新值。
*/
#include 
#include 
#include "sll_node.h"
#define   FALSE    0
#define   TRUE        1
int
sll_insert( register Node **linkp, int new_value )
{
     register Node  *current;
     register Node  *new;
     /*
     ** 寻找正确的插入位置，方法是按序访问链表，直到到达一个其值大于或等于
     ** 新值的节点。
     */
     while( ( current = *linkp ) != NULL &&
         current->value < new_value )
           linkp = ¤t->link;
     /*
     ** 为新节点分配内存，并把新值存储到新节点中，如果内存分配失败，
     ** 函数返回FALSE。
     */
     new = (Node *)malloc( sizeof( Node ) );
     if( new == NULL )
          return FALSE;
     new->value = new_value;
     /*
     ** 在链表中插入新节点，并返回TRUE。
     */
     new->link = current;
     *linkp = new;
     return TRUE;
}

程序12.3 插入到一个有序的单链表：最终版本insert3.c

消除特殊情况使这个函数更为简单。这个改进之所以可行，是由于两个因素。第一个因素是我们正确解释问题的能力。除非可以在看上去不同的操作中总结出共性，不然只能编写额外的代码来处理特殊情况。通常，这种知识只有在学习了一阵数据结构并对其有进一步的理解之后才能获得。第二个因素是C语言提供了正确的工具，可以帮助我们归纳问题的共性。

这个改进的函数依赖于C能够取得现存对象的地址这一能力。和许多C语言特性一样，这个能力既威力巨大，又暗伏凶险。例如，在Modula和Pascal中并不存在“取地址”操作符，所以指针唯一的来源就是动态内存分配。我们没有办法获得一个指向普通变量的指针或甚至是指向一个动态分配的结构的字段的指针。对指针不允许进行算术运算，也没有办法把一种类型的指针通过强制类型转换为另一种类型的指针。这些限制的优点在于它们可以防止诸如“越界引用数组元素”或“产生一种类型的指针但实际上指向另一种类型的对象”这类错误。

C的指针限制要少得多，这也是我们能改进插入函数的原因所在。另一方面，C程序员在使用指针时必须加倍小心，以避免产生错误。Pascal语言的指针哲学有点类似下面这样的说法：“使用锤子可能会伤着你自己，所以我们不给你锤子。”C语言的指针哲学则是：“给你锤子，实际上你可以使用好几种锤子。祝你好运！”有了这个能力之后，C程序员较之Pascal程序员更容易陷入麻烦，但优秀的C程序员可以比Pascal和Modula程序员产生体积更小、效率更高、可维护性更佳的代码。这也是C语言在业界为何如此流行以及经验丰富的C程序员为何如此受青睐的原因之一。

12.2.2 其他链表操作

为了让单链表更加有用，我们需要增加更多的操作，如查找和删除。但是，用于这些操作的算法非常直截了当，很容易用插入函数所说明的技巧来实现。因此，这里把这些函数留作练习。