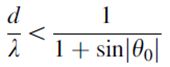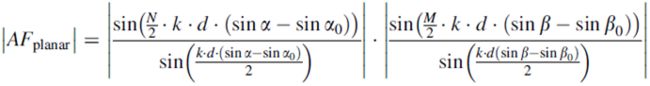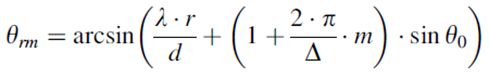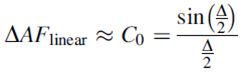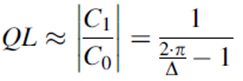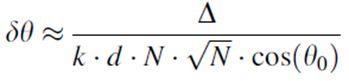天线阵列车载应用——第2章 典型阵列几何形状和基本波束控制方法 2.5节 电子控制相控阵的阵列因子

2.5 电子控制相控阵的阵列因子

2.5.1 模拟移相器设计

       电子束控制的线性无源相控阵示意图如图1.7a所示。线性系统由N个等间隔的相同各向同性阵元组成。每个移相器都有一个特殊的电气控制电路，可以改变接收信号的相位。假设等间距线性天线阵列各阵元之间的间距为d，我们希望接收到来自角度方向为θ0的信号。假设电子控制的移相器在相邻的天线阵元Δδ=Δδ(θ0)之间提供渐进的相移，那么

        （2.18）

       均匀幅度分布的线性天线阵列因子(2.1)可表示为

         (2.19)

       式(2.19)在角度方向θ=θr上的最大值为N

         （2.20）

       r=0对应主波束角度位置(θ=θ0)，r≠0确定栅瓣不需要的瓣的角度位置。

       由式(2.20)可以看出，在可见空间中，最近的不需要的栅瓣不会出现，当

         (2.21)

       让我们假设扫描角度范围等于|θ0|<60°。式(2.21)表示本例中阵元间距d<0.53λ。因此，为了避免在-60到+60度的扫描角扇区出现栅瓣，我们必须选择约为0.53λ的阵元间距，而不是更大。

       等间距平面阵列阵列因子的绝对值由式给出

           (2.22)

       其中sinα=sinθ*cosφ; sinα0=sinθ0*cosφ0; sinβ=sinθ*sinφ; sinβ0=sinθ0*sinφ0。

       为了避免板侧方向扫描角度α0=±60°或β0=±60°的栅瓣，有必要选择沿x和y坐标<0.53λ的间距。

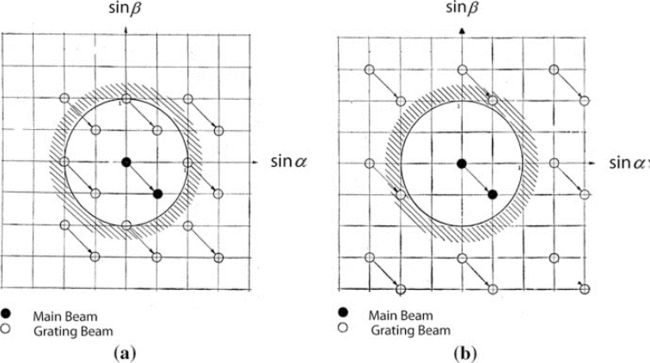
        图2.5显示了可见光范围内栅波束的数量随扫描角度值α和β的变化。

        图2.5a对应波长相等的阵元之间的间距，图2.5b对应波长的三分之二间距。式(2.22)是对模拟移相器在0°到360°范围内连续变化相位的辐射方向图的估计。这种电子可控移相器非常昂贵，通常不用于实践。

图2.5 图示栅瓣：(a)阵元间距等于λ；(b)阵元间距等于2/3*λ。

2.5.2 数字移相器系统

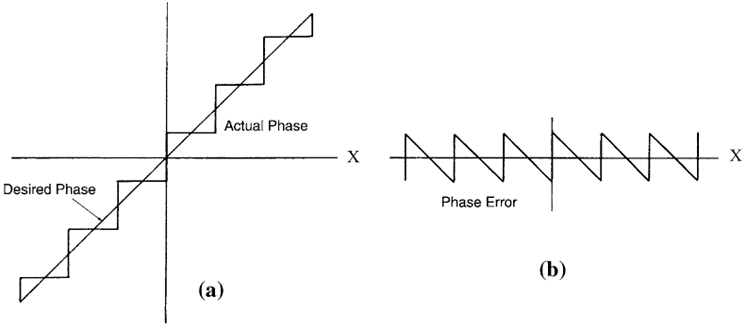
       大多数移相器都是数字控制的，因此它们实现离散Δ的相移，Δ=2*π/2^q，其中q为位数，2^q为数字移相器相态的数量。例如，一个1位(q=1)数字移相器只能产生0°和180°两个相位，一个2位数字移相器可以实现0、π/2、π、3π/2四个相位，一个3位数字移相器可以实现0、π/4、π/2、3π/4、π、5π/4、π/2、7π/4。图2.6a显示了电子扫描的理想(期望)线性相位曲线作为x坐标(沿此轴放置线性阵列)和阶梯相位引起的近似(实际相位)的函数。相位误差如图2.6b所示。

图2.6 (a)电子扫描相移；(b)相位误差函数

       可以看出，理想曲线与其近似值之间的误差是X坐标的周期函数。周期性误差导致主波瓣衰减，产生一组称为“量化波瓣”的波瓣，并引起主波束指向位置误差。由[28,29]可知，带有数字移相器的线性天线阵列的阵列因子可以表示为

           (2.23)

        其中寄生瓣系数Cm由下式给出      

           (2.24)

       由式(2.23)可知，数字移相器阵列的阵列因子为带幅度权重(2.24)的线性阵列因子与波束角度方向之和

         （2.25）

       其中r，m=0，±1，±2…(任何正整数或负整数)。

       具有m = r = 0的阵列因子对应于主波束，而具有m≠0的波束确定不需要的(寄生或量化)波瓣。可以看出，角度方向(2.25)依赖于扫描角θ0，寄生波瓣幅度随着m的增加而减小。数字移相器的主波束损耗效应的简单估计是

          (2.26)

       量化波瓣(QL)值仅依赖于扫描角度位置，而不依赖于阵列幅度分布。量化波瓣QL (m = 1)的最大值[相对于主波瓣(2.26)]等于   

          (2.27)

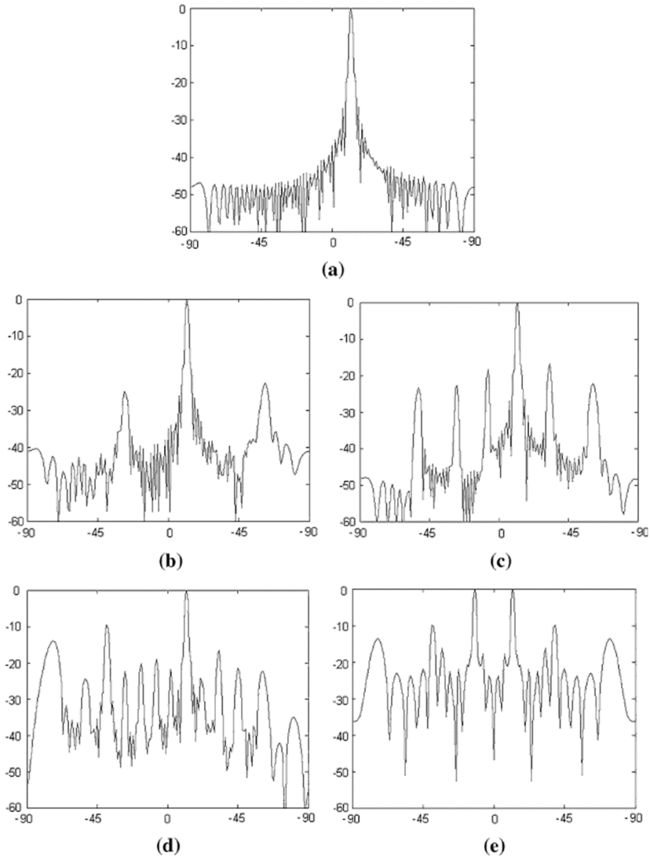
       图2.7给出了等间距(d/λ=0.5)阵元(N = 64)的线性阵列因子的计算机结果。从法线到阵列的扫描角度θ0等于12°，其中与阵列的法线(方向z)对应的角度为0°。振幅分布提供副瓣电平<-20dB。图2.7a为模拟移相器的结果，图2.7b-e为采用数字移相器的同一天线的阵列因子。正如我们所看到的，具有一位移相器的线性阵列因子导致波束被分割成两个相等的主瓣。寄生波瓣的水平和角度位置的计算值与式(2.24)-式(2.27)近似对应。

        图2.7 64阵元线性阵列计算机仿真，间距λ/2，扫描角度12°：(a)模拟移相器；(b) Δ=22.5°；(c) Δ=45°；(d) Δ=90°；(e) Δ=180°。

       [28-32]提出了几种不同的方法来减少这些寄生波瓣。采用图1.7c, d所示的馈电网络可以实现最简单有效的方法之一。带数字移相器的天线阵列被边缘与中心阵元相位差约为360°的球形波辐射。根据已知的阵列几何形状，可以计算出将球形波转化为平面波前所需的相移，也可以计算出扫描波束沿阵列孔径向预定角度方向的线性相移。在这种情况下，辐射相位与数字移相器实现的相位[32]之间的周期性误差被破坏，寄生波瓣显著减少。如果辐射波沿阵列呈准随机相位分布(例如在-180°-180°范围内均匀随机相位分布)，也可以获得类似的效果。这种相位分布可以通过特殊的馈电网络设计来产生。补偿馈电网络相位所需的随机相位存储在计算机存储器中，不依赖于扫描角度。图2.8是在图2.6a所示的阵列相位误差采用随机相位消除，扫描角为12°的情况下，由132个阵元组成的天线阵列线阵因子的仿真结果。图2.8a、b显示了3位移相器的线性阵列因子有和没有随机相位误差的情况，图2.8c、d显示了2位移相器的相似曲线。我们可以看到，随机化周期性相位误差显著减少了寄生波瓣，同时增加了平均功率旁瓣电平Paverage

         (2.28)

       该值是一个粗略估计，可用于多元天线阵列。

        多元阵列主波束指向误差可估计为[15]

           (2.29)

        其中θ0=扫描角度。

        对于小阵元阵列，表达式(2.28)必须通过计算机仿真来修改。

        图2.8 具有随机化周期相位误差的132元线性阵列因子的仿真结果：(a)无随机化的3位移相器;(b)随机化的3位移相器;(c)无随机化的2位移相器;(d)随机化的2位移相器

        以表2.2[33]为例，给出了单元间空间为λ/2、采用1位数字移相器的8元阵列的详细相位分布。

        使用1位移相器，相位被限制在两个状态:0°和180°。天线阵元引导波束所需的最大相位偏差为90°。只有7个相位分布可覆盖60°扫描范围。

        正如我们所看到的，在0°到9°的扫描角度范围内，所有的阵列阵元都是同相的，并且在这个角度范围内没有波束转向。注意，在θ0>9°无法达到最大功率值，因为存在相对于板侧方向对称的两个主瓣。

        2位移相器(q = 2)提供0 - 360°相位范围内的4种相位状态:0°、90°、180°和270°。每个阵元引导波束所需的最大偏差为45°。扫描角度从21°到30°和从30.5°到40.5°，阵列因子值不会改变。

        一个3位移相器(q = 3)给出了8种可能的相位状态，从0°到45°。每个阵元相位的最大偏差为22.5°。波束指向在最大角度范围内保持不变:43°-49°和49°-55.5°。

        一个4位移相器对应于16个相位步进，其离散等于22.5°。相位的最大偏差现在是11.25°。表2.3总结了具有2位移相器到5位移相器的8元阵列的平均阵列因子参数。通过考虑扫描角度从0°到60°，步长为0.5°来实现平均值。扫描角偏差δθ0以度表示，SLmax为旁瓣电平最大值，Dloss为平均指向性损耗。

表2.2 1位移相器可能的相位状态

表2.3 平均线性阵列因子参数

2.5.3 引脚二极管数字移相器拓扑

        电磁波通过信道传播时，其相位发生变化，该信道包括移相器装置。移相器的主要参数是频率范围、带宽、总相位方差、插入损耗和开关速度。基于传输线设计和引脚二极管元件的最简单移相电路如图2.9所示。

        通过在L1和L2两条线之间切换信号，可以实现特定的相移[34]:

           （2.30）

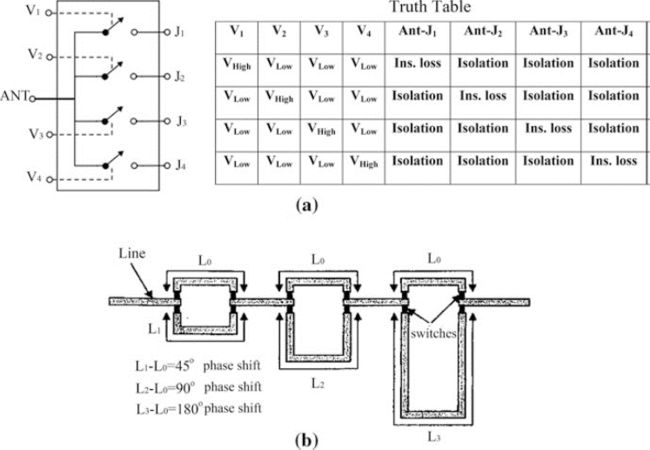
        开关线移相器通常是具有离散（相位）Δ=2*π/2^q的数字阵元。例如，为了获得180°相移，所需的物理长度差ΔL=L2-L1应该是λ/2，为了提供等于90°的相移，需要有λ/4的物理长度差，并且对于45°相位ΔL=λ/8。通常，数字移相器使用PIN二极管作为相位控制元件，因为它们的高速开关时间(几微秒)和相对简单的偏置电路。PIN二极管的插入损耗约为1-3 dB，具体取决于频率范围。市售引脚二极管开关组件按不同的输出数量分类:SPST(一个输入，一个输出)，SPDT(一个输入，两个输出)，SP3T(一个输入，三个输出)等。引脚二极管真值表显示了当输入线与输出线连接以提供所需相移时可控制的电压值(高或低)。基于SP4T开关的2位移相器的框图示例如图2.9d所示，该开关的真值表如图2.10a所示。

        控制电压VHigh等于5伏，VLow为0伏。隔离度对应损耗为30db，插入损耗为<1.5 dB。图2.10b显示了一个使用SPDT集成电路的2位开关线移相器。市场上有许多商用引脚二极管开关，例如，来自Skyworks Solutions, RF Micro Devices, Avago Technologies等。

图2.9移相器电路拓扑：(a)-(c)传输线设计;(d) SP4T交换机配置

图2.10 (a) SP4T开关真值表;(b) 三位开关线移相器