最小生成树超详细介绍
目录
一.最小生成树的介绍
1.最小生成树的简介
2.最小生成树的应用
3.最小生成树的得出方法
二.Kruskal算法
1.基本思想:
2.步骤:
3.实现细节:
4.样例分析:
5.Kruskal算法代码实现:
三.Prim算法
1.基本思想:
2.步骤:
3.实现细节:
4.样例分析:
5.Prim算法代码实现
四.总结
一.最小生成树的介绍
1.最小生成树的简介
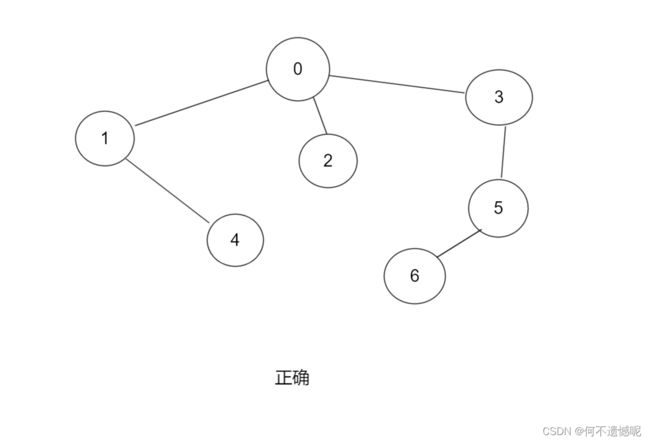
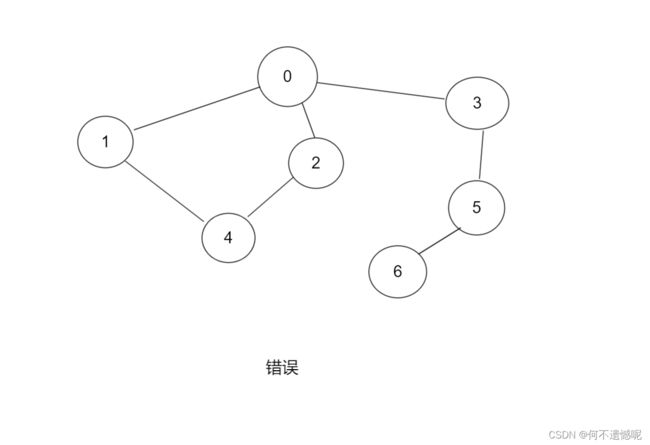
最小生成树(Minimum Spanning Tree,简称MST,在一个连通的无向图,最小生成树是指包含图中所有顶点的一棵树,且该树的所有边的权重之和最小,关键在于树和最小两个关键。
在上面的示例图中我们知道了生成的数是不能有闭环的,那么我们怎么去理解最小的意思。
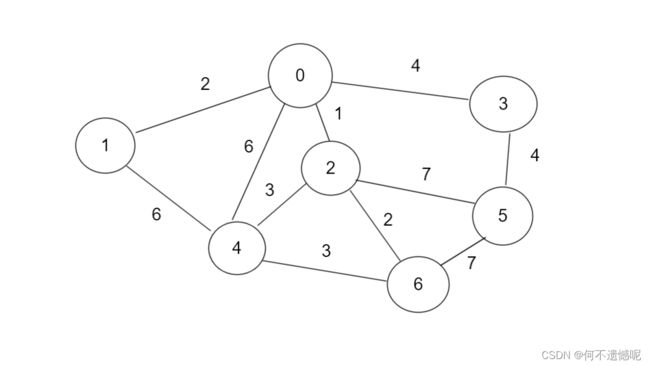
其实在每个点之间相连接的边中是有边的长度的,如下:
我们需要找出的边构成生成树,并且包含图中的所有顶点,使得边的权重之和最小。
2.最小生成树的应用
那么我们很好奇,我们为什么要去寻找这么一个最小生成树呢?
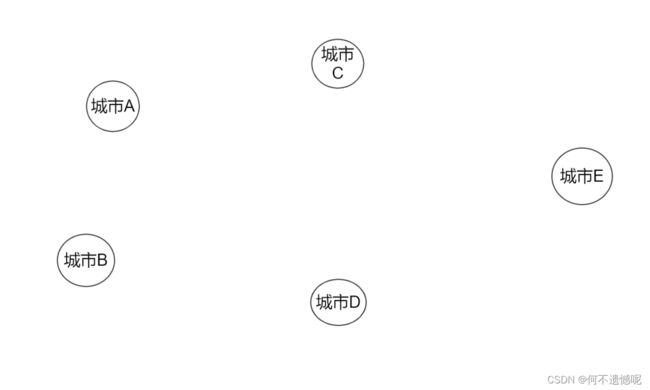
设想,面对一个交通落后的城市
在当今经济发展迅速的阶段,国家肯定不允许城市之间没有一条公路将各个城市串通起来,但是也不会盲目乱铺设,因为人力和成本是很多的,那么串通每个城市之间的公路就是边,我们利用最小生成树将这些城市串通起来的同时,也减少了成本的浪费,这个就是最小生成树的应用之一。
最小生成树在现实应用中具有广泛的用途。一主要应用领域是网络设计,例如通信网络和计算机网络的规划。通过选择最小生成树,可以确保网络中的节点连接最优,减少通信成本。在城市规划中,最小生成树被用于设计交通网络,确保道路布局经济高效。电力系统规划也借助最小生成树,以建立最优的电力输送网络。此外,在电路板设计、社交网络分析以及物流规划等领域,最小生成树都能提供有效的解决方案,降低资源消耗,提高系统效率。这些应用反映了最小生成树作为一种优化工具在解决各种连接和布线问题上的重要性。
3.最小生成树的得出方法
找出最小生成树有这么两个方法。
Kruskal算法和Prim算法。
虽然是两个方法,但是都有使用了贪心的思想。
下面将对两个方法进行详介。
二.Kruskal算法
1.基本思想:
- 将图中所有的边按照权值从小到大排序。
- 从小到大遍历排序后的边,如果边的两个端点不在同一个连通分量中,则将这条边加入最小生成树中,并将这两个端点合并为一个连通分量。(也就是新加的边不能与其他边构成环)
2.步骤:
- 对图中所有边按照权值进行排序。
- 初始化一个空的最小生成树。
- 依次考察排序后的边,如果加入某条边不形成环,则将其加入最小生成树中。
3.实现细节:
- 使用并查集(Disjoint Set)来管理连通分量。
- 可以通过贪心的思想逐步加入边,直到所有顶点都在同一连通分量中为止。(也就是加入的边等于所有的顶点-1)
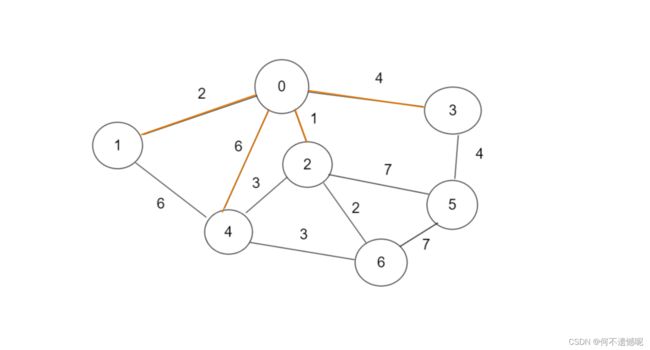
4.样例分析:
我们以这个图为例:
1.先将边按照从小到大分好
2.初始一个空的最小生成树
3.慢慢从小到大填入边
当我们连接4--6时,此时闭成一个环,用红色代表这条边不加入。
此时加入的边为顶点数(7)-1,所以代表已经全部串通,所以最小生成树的边之和就是:
1+2+2+3+4+4=16
5.Kruskal算法代码实现:
首先可以建立一个结构体,里面放上边联通的两个节点和边的长度。
struct node{
int x,y,w;
}a[1000];因为Kruskal算法需要使用到并查集,所以下面是必不可少的Find函数。
int Find(int x)
{
if(pre[x]==x) return x;
return pre[x]=Find(pre[x]);
}由于需要排序,我们这里直接使用c++的sort函数,加上自定义函数cmp
bool cmp(node &x,node &y)
{
return x.w这样就构成了我们的核心函数Kruskal函数。
void Kruskal()
{
sort(a+1,a+1+m,cmp);
for(int i=1;i<=m;i++){
int fx=Find(a[i].x);
int fy=Find(a[i].y);
if(fx==fy) continue;
pre[fx]=fy;
ans+=a[i].w;
cnt++;
if(cnt==n-1)
break;
}
}得到完整代码:
#include
using namespace std;
struct node{
int x,y,w;
}a[1000];
int n,m,ans=0,cnt=0;
int pre[1000];
int Find(int x)
{
if(pre[x]==x) return x;
return pre[x]=Find(pre[x]);
}
bool cmp(node &x,node &y)
{
return x.w>n>>m;
for(int i=1;i<=n;i++){
pre[i]=i;//初始化
}
for(int i=1;i<=m;i++){
cin>>a[i].x>>a[i].y>>a[i].w;
}
Kruskal();//进入核心代码
if(cnt==n-1)
cout< 我们输出来试试看,是不是得到答案16。
三.Prim算法
1.基本思想:
- 选择一个起始顶点,然后逐步选择与当前生成树相邻的权值最小的边,并将连接的顶点加入生成树。
- 重复以上步骤,直到生成树包含图中的所有顶点。
2.步骤:
- 从任意顶点开始,初始化一个空的最小生成树。
- 选择一个与当前生成树相邻的边中权值最小的边,将其连接的顶点加入最小生成树。
- 重复上述步骤,直到最小生成树包含了所有顶点。
3.实现细节:
- 使用优先队列(最小堆)来维护当前生成树与其余顶点之间的边。
- 根据贪心策略,每次选择权值最小的边。
4.样例分析:
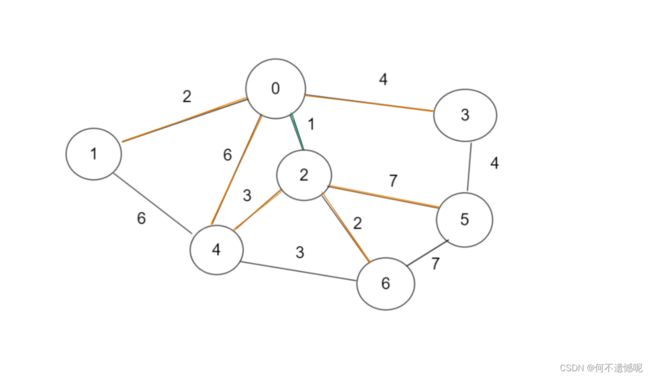
还是以这个图为例子
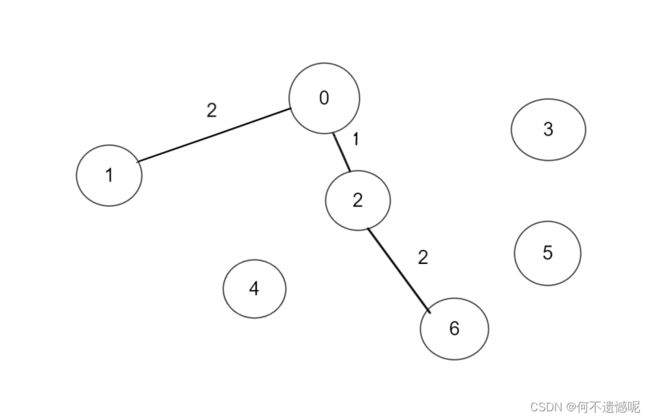
以0这个节点出发,我们有四条边可以加入。
我们选择这最小的。
然后从0和2这两个点出发,继续寻找,发现有两个2,我们选其中一个就行。
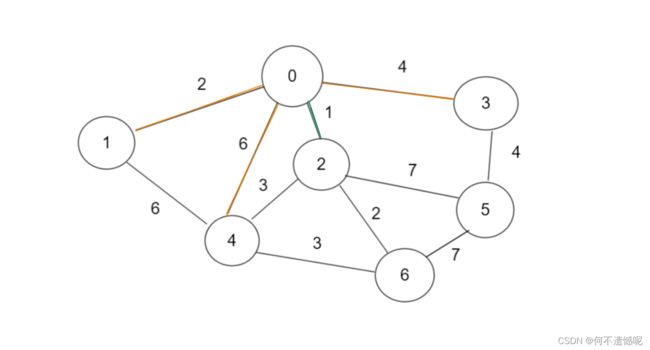
按照这种规则下去,我们得到了最小生成树,红色边是由于构成了闭环而没有使用的边,,绿色为使用的边。
我们来计算一下使用到的所有边的长度:
1+2+2+3+4+4=16。
我们发现这个就是我们前得到的答案。
5.Prim算法代码实现
首先生成最小堆。
struct node
{
int u, w; // u是节点,w是花费
bool operator < (node x) const
{
return w > x.w;
} //重载运算符,生成最小堆
};将每个顶点初始化为无穷大
for(int i = 0; i < n; i++)
dis[i] = INF; // 初始化dis[]加边函数
void add(int u, int v, int w)
{
a[++num].to = v;
a[num].w = w;
a[num].next = head[u];
head[u] = num;
} // 加边得到完整代码:
#include
using namespace std;
const int INF = 1e9;
struct data
{
int to, next, w;
} a[400002]; //链式前向星
struct node
{
int u, w; // u是节点,w是花费
bool operator < (node x) const
{
return w > x.w;
} //重载运算符,生成最小堆
};
int dis[200010], head[200010], num;// dis是最小花费,head存边,num为边数
bool vis[200010];
int n, m, ans = 0, cnt = 0;
void add(int u, int v, int w)
{
a[++num].to = v;
a[num].w = w;
a[num].next = head[u];
head[u] = num;
} // 加边
priority_queue q;
void Prim()
{
q.push((node) {0, 0});
while(!q.empty()||cnt < n) // 进行n-1次
{
node x = q.top();
q.pop();
if(vis[x.u]) continue;
vis[x.u] = true;
cnt++;
ans += x.w;
for(int i = head[x.u]; i ; i = a[i].next)
if(a[i].w < dis[a[i].to]) {
dis[a[i].to] = a[i].w;
q.push((node) {a[i].to, a[i].w});
}
}
}
int main()
{
cin>>n>>m;
for(int i = 1; i <= m; i++)
{
int u, v, w;
cin>>u>>v>>w;
add(u, v, w); add(v, u, w); // 需要加两次无向图
}
for(int i = 0; i < n; i++)
dis[i] = INF; // 初始化dis[]
Prim();
if(cnt==n)
cout< 我们输出一下试试。
代码得到正确答案。
四.总结
- Kruskal更适合稀疏图,因为它按照边的权值排序,而不考虑顶点的度。
- Prim更适合稠密图,因为它按照顶点的度增长来选择边,每次选择与当前生成树相邻的最小权值边。
- Kruskal的时间复杂度主要取决于对边进行排序的时间,通常为O(E log E)
- Prim的时间复杂度通常为O(E log V)。
里面的E为边的数量,V为顶点的数量。
是不是已经完美掌握了。
赶紧去练练题目,来巩固一下知识。
P3366 【模板】最小生成树 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
P1194 买礼物 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
最小生成树就介绍到这里。
本篇完~