python案例——算法入门10例
目录
1、车牌搜寻
2、兔子产子
3、牛顿迭代求方程根
4、百钱百鸡
5、借书方案
6、打鱼晒网
7、最佳存款方案
8、冒泡排序
9、折半查找
10、数制转换
1、 车牌搜寻
题目描述:
卡车违反交通规则,撞人后逃跑。现场有三人目击该事件,但都没有记住车号,只记下了车号的一些特征。甲说:牌照的前两位数字是相同的; 乙说:牌照的后两位数字是相同的,但与前两位不同; 丙是数学家,他说: 4位的车号刚好是一 个整数的平方。请根据以上线索求出车号。
代码实现:
for i in range(32,100):
for a in range(1,9):
for b in range(1,9):
if (1100*a+11*b == i*i)&(a != b):
print(f"{a}{a}{b}{b}")
77442、兔子产子
题目描述:
有对兔子,从出生后的第3个月起每个月都生一对兔子。 小兔子长到第3个月后每个月又生一对兔子, 假设所有的兔子都不死,问30个月内每个月的兔子总对数为多少?
问题分析:
根据推导,每个月兔子总数为:1、1、2、3、5、8、13···,可以得到其就是斐波那契数列,是典型的迭代循环。
代码实现:
fib1 = 1
fib2 = 1
for i in range(3,31):
fib = fib1 +fib2
fib1 = fib2
fib2 = fib
i += 1
print(f"{fib}")
832040用递归的方法同样可以实现:
def fib(n):
if n == 1 or n == 2:
return 1
else:
return fib(n-1)+fib(n-2)
fib(30)
8320403、牛顿迭代求方程根
题目描述:
有方程为 ![]() ,系数a、b、c、d由主函数输入,求x在1附近的实根。求出根后,由主函数输出。
,系数a、b、c、d由主函数输入,求x在1附近的实根。求出根后,由主函数输出。
问题分析:
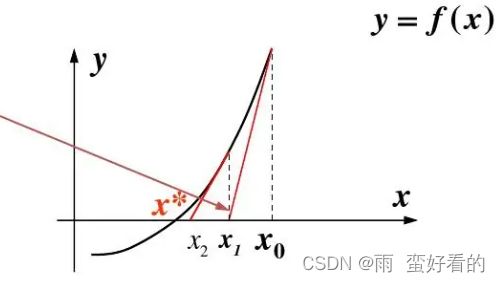
牛顿迭代法求根,就是利用选取的一个点进行切线,然后切线与X轴的交点横坐标x1,再找x1在函数中对应的 f(x1),在做切线,其中切线的方程为 y= f(x0) +fd(x0)(x-x0),找与横轴的交点 x2,x2=x0 - f(x0)/fd(x0),不断做切线找交点,再在函数中找到相应点继续做切线,不断近似求得根,设迭代 | x-x0 | < 10^-5 时结束,认为是方程的根。
代码实现:
def solution(a,b,c,d):
x = 1.5
x0 = x
f = a*x0*x0*x0+b*x0*x0+c*x0+d
fd = 3*a*x0*x0+2*b*x0+c
h = f / fd
x = x0 - h
while abs(x - x0) >= 1e-5:
x0 = x
f = a*x0*x0*x0+b*x0*x0+c*x0+d
fd = 3*a*x0*x0+2*b*x0+c
h = f/fd
x = x0 - h
return x
a,b,c,d = map(float,input().split()) #split()按空格进行拆分,然后进行输入,再映射为浮点类型
2 -4 3 -6
solution(a,b,c,d)
2.0000000000163607 #求解的根4、百钱百鸡
题目描述:
一只公鸡值五钱,一只母鸡值三钱,三只小鸡值一钱,现在用百钱买百鸡,问公鸡母鸡小鸡各多少只
问题分析:
其中公鸡在0-20之内,母鸡在0-33之内,由于题目要求100只,所以不能只买公鸡。
代码实现:
for a in range(0,20):
for b in range(0,33):
for c in range(0,100):
if (a+b+c==100)&(5*a+3*b+c/3==100):
print(f"公鸡{a},母鸡{b},小鸡{c}")
公鸡0,母鸡25,小鸡75
公鸡4,母鸡18,小鸡78
公鸡8,母鸡11,小鸡81
公鸡12,母鸡4,小鸡845、借书方案
题目描述:
小明有5本书,借给A、B、C三个人,每人只能借一本,则可以有多少种解法
问题分析:
每人只能借一本,且相互之间不重复,将书定义为12345。
代码实现:
i=0
for A in range(1,6):
for B in range(1,6):
for C in range(1,6):
if (A!=B)&(B!=C)&(A!=C):
print(f"A借阅:{A},B借阅:{B},C借阅:{C}",end = ' ')
i+=1
if i%3==0:
print()
print(f"共有{i}种借阅方案")
A借阅:1,B借阅:2,C借阅:3 A借阅:1,B借阅:2,C借阅:4 A借阅:1,B借阅:2,C借阅:5
A借阅:1,B借阅:3,C借阅:2 A借阅:1,B借阅:3,C借阅:4 A借阅:1,B借阅:3,C借阅:5
A借阅:1,B借阅:4,C借阅:2 A借阅:1,B借阅:4,C借阅:3 A借阅:1,B借阅:4,C借阅:5
A借阅:1,B借阅:5,C借阅:2 A借阅:1,B借阅:5,C借阅:3 A借阅:1,B借阅:5,C借阅:4
A借阅:2,B借阅:1,C借阅:3 A借阅:2,B借阅:1,C借阅:4 A借阅:2,B借阅:1,C借阅:5
A借阅:2,B借阅:3,C借阅:1 A借阅:2,B借阅:3,C借阅:4 A借阅:2,B借阅:3,C借阅:5
A借阅:2,B借阅:4,C借阅:1 A借阅:2,B借阅:4,C借阅:3 A借阅:2,B借阅:4,C借阅:5
A借阅:2,B借阅:5,C借阅:1 A借阅:2,B借阅:5,C借阅:3 A借阅:2,B借阅:5,C借阅:4
A借阅:3,B借阅:1,C借阅:2 A借阅:3,B借阅:1,C借阅:4 A借阅:3,B借阅:1,C借阅:5
A借阅:3,B借阅:2,C借阅:1 A借阅:3,B借阅:2,C借阅:4 A借阅:3,B借阅:2,C借阅:5
A借阅:3,B借阅:4,C借阅:1 A借阅:3,B借阅:4,C借阅:2 A借阅:3,B借阅:4,C借阅:5
A借阅:3,B借阅:5,C借阅:1 A借阅:3,B借阅:5,C借阅:2 A借阅:3,B借阅:5,C借阅:4
A借阅:4,B借阅:1,C借阅:2 A借阅:4,B借阅:1,C借阅:3 A借阅:4,B借阅:1,C借阅:5
A借阅:4,B借阅:2,C借阅:1 A借阅:4,B借阅:2,C借阅:3 A借阅:4,B借阅:2,C借阅:5
A借阅:4,B借阅:3,C借阅:1 A借阅:4,B借阅:3,C借阅:2 A借阅:4,B借阅:3,C借阅:5
A借阅:4,B借阅:5,C借阅:1 A借阅:4,B借阅:5,C借阅:2 A借阅:4,B借阅:5,C借阅:3
A借阅:5,B借阅:1,C借阅:2 A借阅:5,B借阅:1,C借阅:3 A借阅:5,B借阅:1,C借阅:4
A借阅:5,B借阅:2,C借阅:1 A借阅:5,B借阅:2,C借阅:3 A借阅:5,B借阅:2,C借阅:4
A借阅:5,B借阅:3,C借阅:1 A借阅:5,B借阅:3,C借阅:2 A借阅:5,B借阅:3,C借阅:4
A借阅:5,B借阅:4,C借阅:1 A借阅:5,B借阅:4,C借阅:2 A借阅:5,B借阅:4,C借阅:3
共有60种借阅方案6、打鱼晒网
题目描述:
某人从1990年1月1日开始三天打鱼两天晒网,问这个人在以后的某一天中是大于还是晒网
问题分析:
- 计算指定日期到1990年有多少天
- 天数除以5取余
- 根据余数判断
代码实现:
def myfunc(day):
if day % 5 == 4 or day %5 == 0:
print("这天我在晒网啦")
else:
print("这天我正在打鱼")
print("请输入指定日期:")
a,b,c = map(int,input().split('.'))
print(f"指定日期为{a}年{b}月{c}日")
myfunc(c)
请输入指定日期:
1990.1.8
指定日期为1990年1月8日
这天我正在打鱼7、最佳存款方案
题目描述:
假设银行一年的整存零取的月息为0.63%,现在某人手中有一笔钱,打算今后5年终的每年年底取出1000元,到第五年时刚好取完,问存钱时应存多少。
问题分析:
| 年初存款 | 公式 |
| 第5年年初时的存款 | |
| 第4年年初时的存款 | |
| 第3年年初时的存款 | |
| 第2年年初时的存款 | |
| 第1年年初时的存款 |
代码实现:
"""递归法"""
def myfunc(n):
if n==1:
return 1000/(1+12*0.0063)
else:
return (1000+myfunc(n-1))/(1+12*0.0063)
myfunc(5)
"""迭代法"""
i = 0
money = 0
while i<5:
money = (money+1000)/(1+12*0.0063)
i+=1
print(f"钱为{money}")
"""编译器"""
def myfunc(n):
if n==1:
return 1000/(1+12*0.0063)
else:
return (1000+myfunc(n-1))/(1+12*0.0063)
print("请输入年份")
x = int(input())
print(f"年份为{x}")
c = myfunc(x)
print(c)
8、冒泡排序
题目描述:
对N个整数进行升序排列
问题分析:
关于冒泡排序是最基础的交换排序,像小气泡一样根据自己的大小一点一点向一侧移动,每一次比较就会把最大的筛选出来,第一轮比较N-1次
![]()
代码实现:
def bubbleSort(a):
for i in range(0,len(a)-1):
for j in range(0,len(a)-i-1):
if a[j]>a[j+1]:
a[j],a[j+1] = a[j+1],a[j]
return a
x = input()
5 3 9 6 8 2 7
x
'5 3 9 6 8 2 7'
a = x.split()
a
['5', '3', '9', '6', '8', '2', '7']
for i in range(0,len(a)):
x[i] = int(x[i])
bubbleSort(a)
[2, 3, 5, 6, 7, 8, 9]9、折半查找
题目描述:
N个有序整数数列已放在一维数组中,利用二分法查找整数m在数组中的位置,找到输出下标值,没找到输出“NOT BE FOUND”
问题分析:
代码实现:
def myfunc(a,b):
length = len(a)
high = length - 1 #数组上界
low = 0 #数组下界
k=-1 #记录索引值
while low <= high:
mid = int((high+low)/2)
if b < a[mid]:
high = mid - 1
elif b > a[mid]:
low = mid + 1
else:
k = mid
break
if k>=0:
print(f"所找到的元素下标为{k}")
else:
print("NOT BE FOUND")
print("请输入数组:")
a = list(map(int,input().split()))
print(f"输入数组:{a}")
print("输入查找的数:")
b = int(input())
print(f"查找的数{b}")
myfunc(a,b)
10、数制转换
题目描述:
给定一个 M 进制的数 x ,实现对 x 任意一个非 M 进制的数转换。
问题分析:
其他进制转十进制:按权展开相加。
十进制转其他进制:整数部分除以基数再取余(取余从后向前排)小数部分乘以基数取整数
二、八、十六间转换:先转十进制再转换;或者按照对应关系进行转换:3位二进制对应一位八进制,4位二进制对应一位16进制。
算法设计:
十六进制是由 0 - F 这一组固定的数字来表示,所以采用 字符数组 进行存储,在输入输出的时候,数组元素都是 字符 形式存在,而在进行数制的转换时,是以 数字 的形式存在。因此我们还需要用到字符和数字之间的相互转换。
在执行程序时,为了运行1次程序,而可以多次输入数据进行验证,我们设置 flag 标志,“while flag” 控制进行继续输入。
程序框架:
flag = 1
while flag:
#将原数转化为十进制
#十进制转化为其他进制
#逆序打印
flag = int(input())#决定是否继续转换字符与数字的转换:
字符 ’A‘ 对应数字 10,以此类推
- int(x) 其他类型转化为数字
- ord(x) 将字符串转为Unicode码
- str(x) 其他类型转化为字符串
- chr(x) 十进制转化为对应字符
代码实现:
#字符串转数字
def char_to_num(ch):
if ch >= '0' and ch <= '9':
return int(ch)
else:
return ord(ch)
#数字转字符串
def num_to_char(num):
if num >= 0 and num <= 9:
return str(num)
else:
return chr(num)
#其他进制转十进制
def source_to_decimal(temp,source):
decimal_num = 0 #存储展开之后的和
for i in range(len(temp)): #累加
decimal_num = (decimal_num * source) + char_to_num(temp[i])
return decimal_num
#十进制转其他进制
def decimal_to_object(decimal_num,object):
decimal=[]
while decimal_num:
decimal.append(num_to_char(decimal_num % object))
decimal_num //= object
return decimal
#倒叙输出
def output(decimal):
f = len(decimal)-1
while f>=0:
print(decimal[f],end=' ')
f -= 1
print()
#主程序
flag = 1 #退出程序的标志
while flag:
print("转换前的数是: ")
temp = input()
print("转换前的数制是")
source = int(input())
print("转换后的数制是")
object = int(input())
print("转换后的数是")
decimal_num = source_to_decimal(temp,source)
decimal = decimal_to_object(decimal_num,object)
output(decimal)
print("继续按1,退出按0")
flag = int(input())