力扣236二叉树的最近公共祖先(c++)
力扣236二叉树的最近公共祖先(c++)
力扣题目链接
思路
遇到这个题目首先想的是要是能自底向上查找就好了,这样就可以找到公共祖先了。
那么二叉树如何可以自底向上查找呢?
回溯啊,二叉树回溯的过程就是从低到上。
后序遍历(左右中)就是回溯过程,可以根据左右子树的返回值,来处理中节点的逻辑。
接下来就看如何判断一个节点是节点q和节点p的公共公共祖先呢。
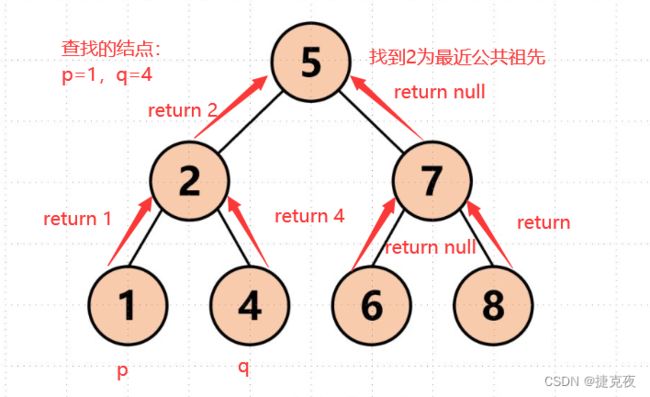
首先最容易想到的一个情况:如果找到一个节点,发现左子树出现结点p,右子树出现节点q,或者 左子树出现结点q,右子树出现节点p,那么该节点就是节点p和q的最近公共祖先。 即情况一:
判断逻辑是 如果递归遍历遇到q,就将q返回,遇到p 就将p返回,那么如果 左右子树的返回值都不为空,说明此时的中节点,一定是q 和p 的最近祖先。
这时我们会想到,会不会左子树 遇到q 返回,右子树也遇到q返回,这样并没有找到 q 和p的最近祖先。
这我们就要审题了,题目强调:二叉树节点数值是不重复的,而且一定存在 q 和 p。
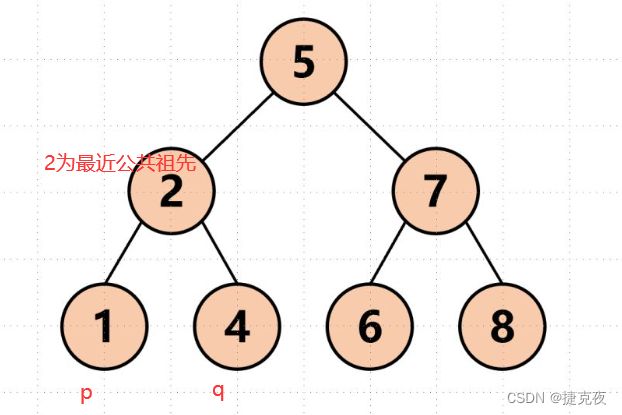
很多人还容易忽略另外一个情况,就是节点本身是p或q,它拥有一个子孙节点q§。 情况二:

其实情况一 和 情况二 代码实现过程都是一样的,也可以说,实现情况一的逻辑,顺便包含了情况二。
因为遇到 q 或者 p 就返回,这样也包含了 q 或者 p 本省就是 公共祖先的情况。
例如上图,第一次遇到p返回p,后来又遇到了q,返回q那么q本身就是最近最近公共祖先,刚好最后返回的也是q。
递归三部曲:
1、确定递归函数返回值以及参数
需要递归函数返回值,来告诉我们是否找到节点q或者p,那么返回值为bool类型就可以了。
但我们还要返回最近公共节点,可以利用上题目中返回值是TreeNode * ,那么如果遇到p或者q,就把q或者p返回,返回值不为空,就说明找到了q或者p。
代码如下:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
2、确定终止条件
遇到空的话,然后返回root,因为树都是空了,所以返回空。
那么我们来说一说,如果 root == q,或者 root == p,说明找到 q p ,则将其返回,这个返回值,后面在中节点的处理过程中会用到。
代码如下:
if (root == q || root == p || root == NULL) return root;
3、确定单层递归逻辑
值得注意的是 本题函数有返回值,是因为回溯的过程需要递归函数的返回值做判断,但本题我们依然要遍历树的所有节点。
如果递归函数有返回值,如何区分要搜索一条边,还是搜索整个树呢?
搜索一条边的写法:
if (递归函数(root->left)) return ;
if (递归函数(root->right)) return ;
搜索整个树写法:
left = 递归函数(root->left); // 左
right = 递归函数(root->right); // 右
left与right的逻辑处理; // 中
在递归函数有返回值的情况下:如果要搜索一条边,递归函数返回值不为空的时候,立刻返回,如果搜索整个树,直接用一个变量left、right接住返回值,这个left、right后序还有逻辑处理的需要,也就是后序遍历中处理中间节点的逻辑(也是回溯)。
那么为什么要遍历整棵树呢?直观上来看,找到最近公共祖先,直接一路返回就可以了。
如图:
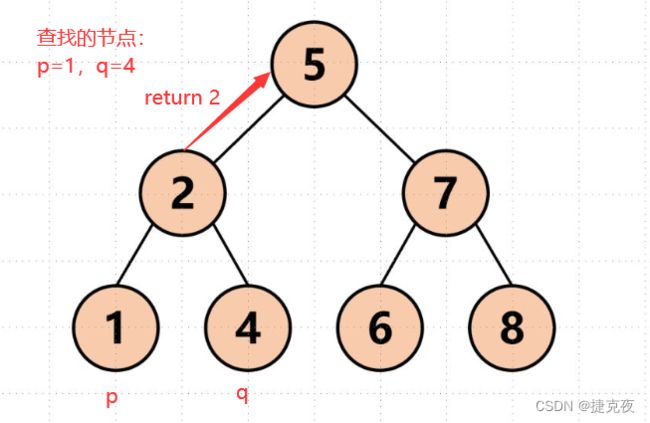
就像图中一样直接返回2,多方便。
但事实上还要遍历根节点右子树(即使此时已经找到了目标节点了),也就是图中的节点1、4、2。
因为在如下代码的后序遍历中,如果想利用left和right做逻辑处理, 不能立刻返回,而是要等left与right逻辑处理完之后才能返回。
left = 递归函数(root->left); // 左
right = 递归函数(root->right); // 右
left与right的逻辑处理; // 中
所以此时大家要知道我们要遍历的是整棵树。
那么先用left和right接住左子树和右子树的返回值,代码如下:
TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);
如果left 和 right都不为空,说明此时root就是最近公共节点。这个比较好理解
如果left为空,right不为空,就返回right,说明目标节点是通过right返回的,left和right交换一下也是如此。
那么我们为什么left为空,right不为空,目标节点要通过right返回呢?
如图:
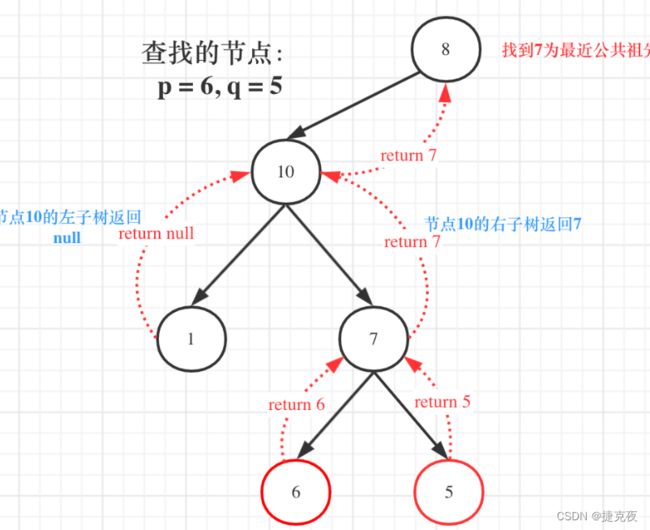
图中节点10的左子树返回null,右子树返回目标值7,那么此时节点10的处理逻辑就是把右子树的返回值(最近公共祖先7)返回上去!
那么如果left和right都为空,则返回left或者right都是可以的,也就是返回空。
代码如下:
if (left == NULL && right != NULL) return right;
else if (left != NULL && right == NULL) return left;
else { // (left == NULL && right == NULL)
return NULL;
}
完整代码
class Solution
{
public:
TreeNode *lowestCommonAncestor(TreeNode *root, TreeNode *p, TreeNode *q)
{
if (root==q||root==p||root==NULL)
return root;
TreeNode *left = lowestCommonAncestor(root->left, p, q);
TreeNode *right = lowestCommonAncestor(root->right, p, q);
if (left!=NULL && right!=NULL) //找到了最近公共祖先
return root;
if(left==NULL&&right!=NULL)
return right;
else if(left!=NULL&&right==NULL)
return left;
else
return NULL;
}
};
总结
1、求最小公共祖先,需要从底向上遍历,那么二叉树,只能通过后序遍历(即:回溯)实现从低向上的遍历方式。
2、在回溯的过程中,必然要遍历整棵二叉树,即使已经找到结果了,依然要把其他节点遍历完,因为要使用递归函数的返回值(也就是代码中的left和right)做逻辑判断。
3、要理解如果返回值left为空,right不为空为什么要返回right,为什么可以用返回right传给上一层结果。
本题没有给出迭代法,因为迭代法不适合模拟回溯的过程。理解递归的解法就够了。