背包问题(01背包、完全背包、多重背包)详解(超详细!!!),及题目代码和题意,包含6个例题。
第一题:01背包问题
01背包问题
时间限制:1秒 内存限制:128M
题目描述
一个旅行者有一个最多能装 M 公斤的背包,现在有 n 件物品,它们的重量分别是 W1,W2,...,Wn ,它们的价值分别为 C1 , C2 ,..., Cn ,求旅行者能获得最大总价值。
输入描述
第一行:两个整数,M (背包容量,M≤200 )和 N (物品数量, N≤30 );
第 2..N+1 行:每行二个整数 Wi,Ci ,表示每个物品的重量和价值。
输出描述
仅一行,一个数,表示最大总价值。
样例
输入
10 4 2 1 3 3 4 5 7 9
输出
12
重要信息筛选
最多能装 M 公斤的背包,现在有 n 件物品,它们的重量分别是 W1,W2,...,Wn ,它们的价值分别为 C1 , C2 ,..., Cn ,求最大总价值。
思路:
对于每个物品有两个选择,放入或者不放,有 n 个物品,所以要做出 n 个选择,可以视为 n个状态阶段。
用 f[n][m]表示有 n 个物品时,放入容量为 m 的背包所能获得的最大价值。样例要求的就是 f[4][10]。
包容量为 10,考虑第 4 个物品(重量为 2,价值为 1),分两种情况:
1)放入第 4 个物品
对应的背包价值为前 3 个物品放在容量为(10-2)的包里的最大价值+第 4 个物品的价值。
f[4][10]=f[3][10-2]+1=f[3][8]+1
f[3][8]代表什么含义呢?
-有前 3 个物品时,放入容量为 8 的背包所能获得的最大价值
-考虑第 3 个物品,同样分为两种情况
a.f[3][8]=f[2][4]+5
b.f[3][8]=f[2][8]
2)不放入第 4 个物品
对应的背包价值和前 3 个物品放在容量为 10 的包里的价值一样。 f[4][10]=f[3][10]
1 和 2 两种情况哪个的背包价值更大,f[4][10]就是哪个值。
用 f[i][j]表示背包中有 i 个物品,重量为 j 时的价值情况,如下图所示:
以 f[2][8]为例, f[2][8]=max(f[1][8-3]+3,f[1][8])
= max(f[1][5]+3,f[1][8])

求 f[2][8]的值时,只需要知道 f[1][8]左侧部分的数据即可。
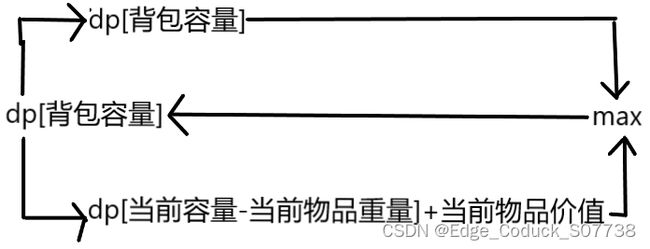
其实把它优化成一维的,也是可行的,因为不用i-1,直接每次求最大值。此时状态转移方程变成这样:
此时,代码主体框架已经完成,完成输入输出即可
AC代码:
#include
using namespace std;
int dp[10000005],w[10005],c[10005];//定义
int main(){
int n,m,cnt=0;
scanf("%d%d",&m,&n);//输入最大容量和数量
for(int i=1; i<=n; i++){
cin>>w[i]>>c[i];//输入重量和
}
for(int i=1;i<=n;i++){//枚举所有物品
for(int j=m;j>=w[i];j--){//枚举从最大容量到当前物品重量
dp[j]=max(dp[j],dp[j-w[i]]+c[i]);//dp[当前容量]=max(dp[当前容量],dp[当前容量-当前物品重量]+当前物品价值);
}
}
printf("%d",dp[m]);//输出
return 0;
} 第二题:采药
采药
时间限制:1秒 内存限制:128M
题目描述
辰辰是个很有潜能、天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。为此,他想拜附近最有威望的医师为师。医师为了判断他的资质,给他出了一个难题。医师把他带到个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同的草药,采每一株都需要一些时间,每一株也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。
如果你是辰辰,你能完成这个任务吗?
输入描述
输入的第一行有两个整数T(1≤T≤1000)和M(1≤M≤100),T代表总共能够用来采药的时间,M代表山洞里的草药的数目。接下来的M行每行包括两个在1到100之间(包括1和100)的的整数,分别表示采摘某株草药的时间和这株草药的价值。
输出描述
输出只包括一行,这一行只包含一个整数,表示在规定的时间内,可以采到的草药的最大总价值。
样例
输入
70 3 71 100 69 1 1 2
输出
3
思路:
转化为T为背包容量,M为物品数量,采药时间看成重量,采药价值看成价值,再套用01背包完成此问题。
对于每个物品有两个选择,放入或者不放,有 n 个物品,所以要做出 n 个选择,可以视为 n个状态阶段。
用 f[n][m]表示有 n 个物品时,放入容量为 m 的背包所能获得的最大价值。样例要求的就是 f[4][10]。
包容量为 10,考虑第 4 个物品(重量为 2,价值为 1),分两种情况:
1)放入第 4 个物品
对应的背包价值为前 3 个物品放在容量为(10-2)的包里的最大价值+第 4 个物品的价值。
f[4][10]=f[3][10-2]+1=f[3][8]+1
f[3][8]代表什么含义呢?
-有前 3 个物品时,放入容量为 8 的背包所能获得的最大价值
-考虑第 3 个物品,同样分为两种情况
a.f[3][8]=f[2][4]+5
b.f[3][8]=f[2][8]
2)不放入第 4 个物品
对应的背包价值和前 3 个物品放在容量为 10 的包里的价值一样。 f[4][10]=f[3][10]
1 和 2 两种情况哪个的背包价值更大,f[4][10]就是哪个值。

用 f[i][j]表示背包中有 i 个物品,重量为 j 时的价值情况,如下图所示:

以 f[2][8]为例, f[2][8]=max(f[1][8-3]+3,f[1][8])
= max(f[1][5]+3,f[1][8])

求 f[2][8]的值时,只需要知道 f[1][8]左侧部分的数据即可。
其实把它优化成一维的,也是可行的,因为不用i-1,直接每次求最大值。此时状态转移方程变成这样:
此时,代码主体框架已经完成,完成输入输出即可
AC代码:
#include
using namespace std;
int dp[10000005],w[10005],c[10005];//定义
int main(){
int n,m,cnt=0;
scanf("%d%d",&m,&n);//输入最大容量和数量
for(int i=1; i<=n; i++){
cin>>w[i]>>c[i];//输入重量和
}
for(int i=1;i<=n;i++){//枚举所有物品
for(int j=m;j>=w[i];j--){//枚举从最大容量到当前物品重量
dp[j]=max(dp[j],dp[j-w[i]]+c[i]);//dp[当前容量]=max(dp[当前容量],dp[当前容量-当前物品重量]+当前物品价值);
}
}
printf("%d",dp[m]);//输出
return 0;
} 第三题:数字组合
数字组合
时间限制:1秒 内存限制:128M
题目描述
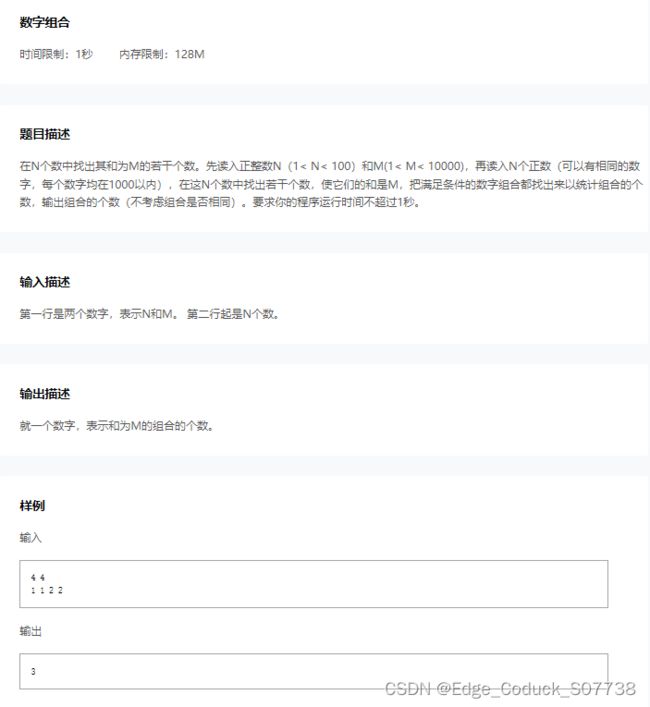
在N个数中找出其和为M的若干个数。先读入正整数N(1< N< 100)和M(1< M< 10000),再读入N个正数(可以有相同的数字,每个数字均在1000以内),在这N个数中找出若干个数,使它们的和是M,把满足条件的数字组合都找出来以统计组合的个数,输出组合的个数(不考虑组合是否相同)。要求你的程序运行时间不超过1秒。
输入描述
第一行是两个数字,表示N和M。 第二行起是N个数。
输出描述
就一个数字,表示和为M的组合的个数。
样例
输入
4 4 1 1 2 2
输出
3
思路:
这是典型的 0/1 背包模型,n 个正整数就是 n 个物品,t 就是背包的容积。
在外层循环到 i 时(表示从前 i 个数中选),设 f[j]表示“和为 j”有多少种方案。在具体实现中,只需要把上面代码中求 max 的函数改为求和即可。
这边为大家奉上代码
#include
using namespace std;
int main(){
int n,m,a[10005],f[10005];
cin>>n>>m;
for(int i=1; i<=n; i++) cin>>a[i];
f[0]=1;
for(int i=1; i<=n; i++){
for(int j=m; j>=a[i]; --j){
f[j]+=f[j-a[i]];
}
}
cout< 第四题:完全背包问题
完全背包问题
时间限制:1秒 内存限制:128M
题目描述
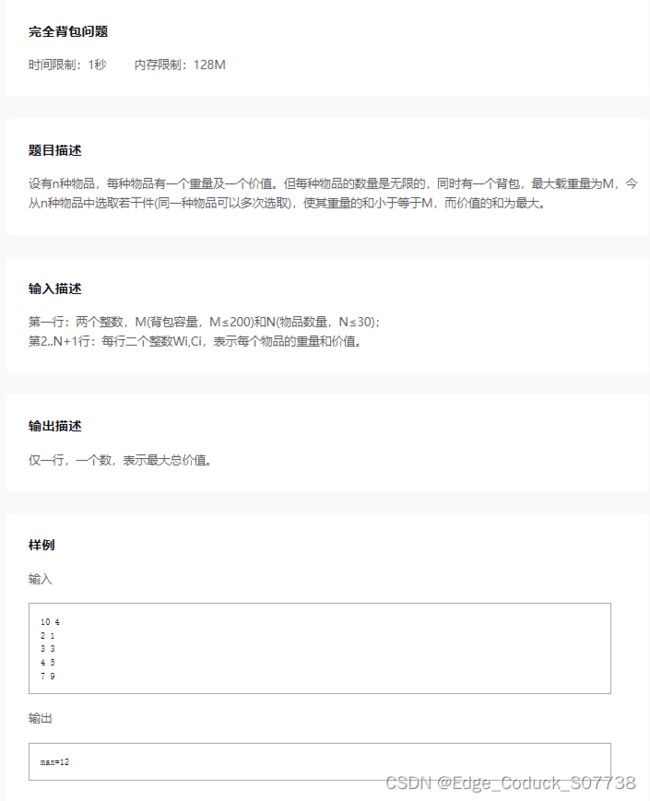
设有n种物品,每种物品有一个重量及一个价值。但每种物品的数量是无限的,同时有一个背包,最大载重量为M,今从n种物品中选取若干件(同一种物品可以多次选取),使其重量的和小于等于M,而价值的和为最大。
输入描述
第一行:两个整数,M(背包容量,M≤200)和N(物品数量,N≤30);
第2..N+1行:每行二个整数Wi,Ci,表示每个物品的重量和价值。
输出描述
仅一行,一个数,表示最大总价值。
样例
输入
10 4 2 1 3 3 4 5 7 9
输出
max=12
思路:
状态为 f[x],表示包容量为 x 时获得的最大价值
放入的最后一个物品可能是重量小于 x 的任何一个,选最大的那个
f[12],包容量为 12 时获得的最大价值
只考虑最后一个物品,分四种情况
1)最后一个是物品①(重量为 2,价值为 1)
f[12]=f[12-2]+1=f[10]+1
2)最后一个是物品②(重量为 3,价值为 3)
f[12]=f[12-3]+3=f[9]+3
3)最后一个是物品③(重量为 4,价值为 5)
f[12]=f[12-4]+5=f[8]+5
4)最后一个是物品④(重量为 7,价值为 9)
f[12]=f[12-7]+9=f[5]+9
找四种情况里最大的那个
f[5],包容量为 5 时获得的最大价值
只考虑最后一个物品,分三种情况
1)最后一个是物品①(重量为 2,价值为 1)
f[5]=f[5-2]+1=f[3]+1
2)最后一个是物品②(重量为 3,价值为 3)
f[5]=f[5-3]+3=f[2]+3
3)最后一个是物品③(重量为 4,价值为 5)
f[5]=f[5-4]+5=f[1]+5
4)最后一个可能是物品④(重量为 7,价值为 9)吗?
所以,根据思路,即可写出代码:
#include
using namespace std;
int f[10000005],w[10005],c[10005];
int main(){
int n,m,cnt=0;
scanf("%d%d",&m,&n);
for(int i=1; i<=n; i++){
cin>>w[i]>>c[i];
}
for(int i=1;i<=n;i++){
for(int j=w[i];j<=m;j++){//01背包是从m到w[i],完全背包是w[i]到m
f[j]=max(f[j],f[j-w[i]]+c[i]);
}
}
printf("max=%d",f[m]);
return 0;
} 第五题:多重背包
多重背包
时间限制:1秒 内存限制:128M
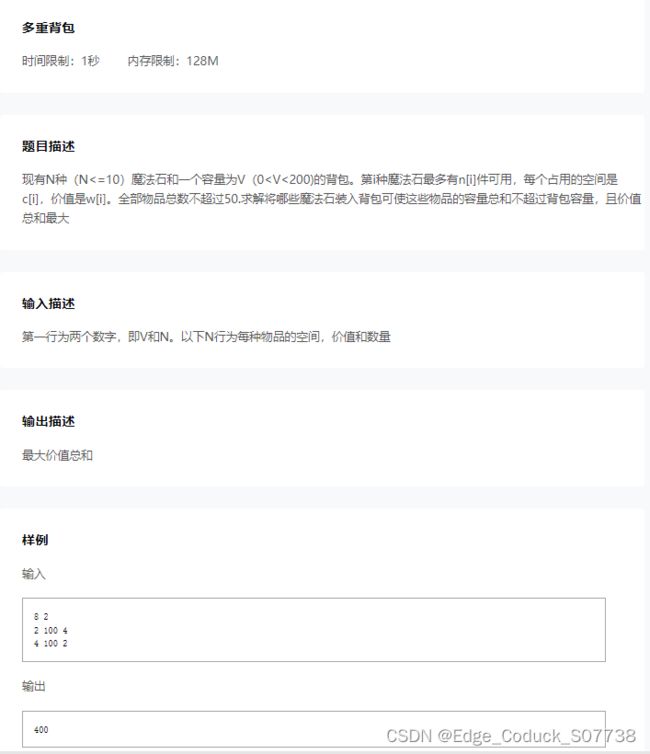
题目描述
现有N种(N<=10)魔法石和一个容量为V(0 第一行为两个数字,即V和N。以下N行为每种物品的空间,价值和数量 最大价值总和 对于每个物品有 ?个选择 时间限制:1秒 内存限制:128M 小明手里有n元钱全部用来买书,书的价格为10元,20元,50元,100元。 问小明有多少种买书方案?(每种书可购买多本) 一个整数 n,代表总共钱数。(0 <= n <= 1000) 一个整数,代表选择方案种数 初始化为:f[0][0] = 1 可达鸭二月月赛——入门赛第四场T1题解 可达鸭二月月赛——入门赛第四场T2题解 可达鸭二月月赛——入门赛第四场T3题解 可达鸭二月月赛——入门赛第四场T4题解 可达鸭二月月赛——入门赛第四场(周三)题解 点个赞吧,求求了,制作不易。输入描述
输出描述
样例
输入
8 2
2 100 4
4 100 2
输出
400
用 f[n][m]表示有 n 个物品时,放入容量为 m 的背包所能获得的最大价值。样例要求的就是 f[2][8]。
包容量为 8,考虑物品②(空间为 4,价值为 100,总量为 2),分 3 种情况1)放入 0 个物品②
f[2][8]=f[1][8]
2)放入 1 个物品②
f[2][8]=f[1][8-4]+100=f[1][4]+100
2)放入 2 个物品②
f[2][8]=f[1][8-4*2]+100*2=f[1][0]+200也可以用一维数组进行优化
程序:#include第六题:买书
买书
题目描述
输入描述
输出描述
样例
输入
20
输出
2
题目分析:
现在有四种类型的书,可以类比成四种物品,重量就是书的价格,可以用完全背包的方法来
求解,但是本题目不是求最大价值,而是求方案数。完全背包问题求解方案数把 max 修改成 sum 就可以了
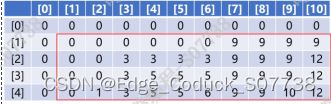
f[i][j]表示前 i 件物品放到背包容量为 j 的背包的方案数
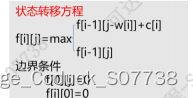
状态转移方程:
f[i][j] += f[i-1][j-w[i]]
也可以用一维优化
f[i]表示放到背包容量为 i 的背包里面总共有多少种方案
状态转移方程:
f[j] += f[j - a[i]];代码:
#include总结:背包问题真难啊
往期回顾: