编译原理实验三 自下而上语法分析

一、实验目的

（1）根据 PL/0 语言的文法规范，要求编写 PL/0语言的语法分析程序。
（2）通过设计、编制、调试一个典型的自下而上语法分析程序，实现对语法分析程序所提供的单词序列进行语法检查和结构分析，进一步掌握常用的语法分析方法。
（3）选择最有代表性的语法分析方法，算符优先分析法、LR分析法；或者调研语法分析器的自动生成工具YACC的功能与工作原理，使用YACC生成一个自底向上的语法分析器。

二、实验内容

（1）已给 PL/0 语言文法，构造表达式部分的语法分析器。
分析对象〈算术表达式〉的 BNF 定义如下：
<表达式> ::= [+|-]<项>{<加法运算符> <项>}
<项> ::= <因子>{<乘法运算符> <因子>}
<因子> ::= <标识符>| <无符号整数> | ‘(’<表达式>‘)’
<加法运算符> ::= +|-
<乘法运算符> ::= *|/

巴科斯范式(BNF)的语法规则：
在双引号中的字(“word”)代表着这些字符本身。而double_quote用来代表双引号。
在双引号外的字（有可能有下划线）代表着语法部分。
尖括号( < > )内包含的为必选项。
方括号( [ ] )内包含的为可选项。
大括号( { } )内包含的为可重复0至无数次的项。
竖线( | )表示在其左右两边任选一项，相当于"OR"的意思。
::= 是“被定义为”的意思。

(2)根据实验一的词法分析的结果进行输入。例如：对于 PL/0 表达式，（a+15）*b 用下列形式作为输入：
 (lparen,( )
 (ident, a)
 (plus, + )
 (number, 15)
 (rparen,) )
 (times, * )
 (ident, b )
输出：
对于语法正确的表达式，输出为“Yes,it is correct.”
对于语法错误的表达式，输出为“No,it is wrong.”

三、设计思想及实验步骤

（一）设计思想
本实验采用算符优先分析法。算符优先分析是定义在算符之间的某种优先关系，借助于这种优先关系寻找可规约串和进行规约。

对于文法G：
 <表达式> ::= [+|-]<项>{<加法运算符> <项>}
 <项> ::= <因子>{<乘法运算符> <因子>}
 <因子> ::= <标识符>|<无符号整数>| ‘(’<表达式>‘)’
 <加法运算符> ::= +|-
 <乘法运算符> ::= *|/
 <关系运算符> ::= =|#|<|<=|>|>=

可以改写如下所示：
  S’-><表达式>
  <表达式>-><项>
  <表达式>-><表达式>+<项>
  <表达式>-><表达式>-<项>
  <项>-><因子>
  <项>-><项>*<因子>
  <项>-><项>/<因子>
  <因子>->(<表达式>)
  <因子>-><标识符>
  <因子>-><无符号整数>

算符文法的定义：
 一个文法，如果它的任一产生式的右部都不含两个相继并列的非终结符，如设有一个文法G，如果G中没有形如A→…BC…的产生式，其中B和C为非终结符，则称G为算符文法。
对于优先关系进行如下定义：
a的优先级小于b
(1) a a的优先级等于b
(2) a=b：当且仅当文法G中有形如P→…ab…或者P→…aQb…的产生式
a的优先级高于b
(3) a>b：当且仅当文法G中有形如P→…Rb…的产生式,而R⇒+…a或R⇒+…aR
如果一个算符文法G中的任何终结符对（a，b）至多满足下述三关系之一：ab，则称G是一个算符优先文法。

从算符优先文法G构造优先关系表：
检查G的每个产生式的每个候选式，可找出所有满足a=b的终结符对，为找出所有满足关系<和>的终结符对，需要对G的每个非终结符P构造两个集合FIRSTVT§和LASTVT§。
定义并构造FIRSTVT和LASTVT两个集合
FIRSTVT§={a|P⇒+a⋯或P⇒+Qa⋯}
LASTVT§={a|P⇒+⋯a或P⇒+⋯aQ}

（二）实验步骤

（1）构造文法G的FIRSTVT集和LASTVT集
文法：
B -> J X(J X)* | X (J X)* （表达式）
X ->Y (C Y)* （项）
Y ->I | N |( B ) （因子）
J -> + | - （加法运算符）
C -> * | / （乘法运算符）

FIRSTVT集:
FIRSTVT(表达式)={+，-，(,， /，标识符，无符号整数 }
FIRSTVT(项)={，/，（，标识符，无符号整数}
FIRSTVT(因子)={(，标识符，无符号整数}
FRTSTVT(加法运算符)={+，-}
FRTSTVT(乘法运算符)={，/}

LASTVT集:
LASTVT(表达式)={+，-,），， /，标识符，无符号整数 }
LASTVT(项)={，/，)，标识符，无符号整数}
LASTVT(因子)={)，标识符，无符号整数}

（2）构造优先关系表

（3）构造总控程序
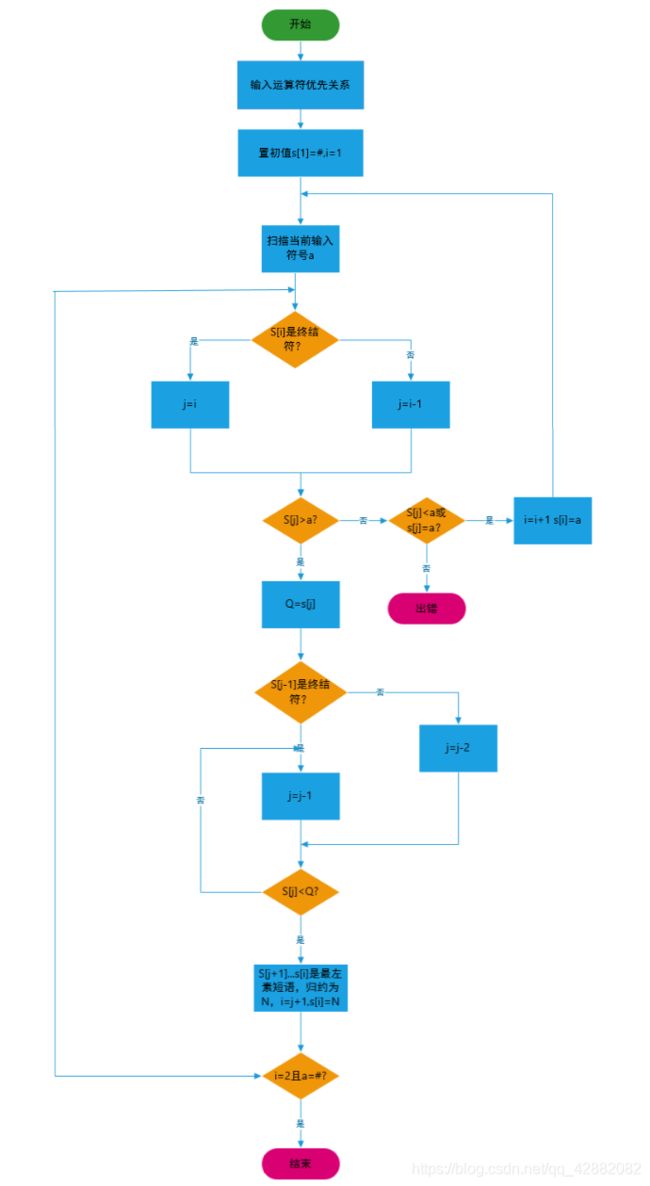
算法优先分析算法描述如下：
stack S;
k = 1; //符号栈S的使用深度
S[k] = ‘#’
REPEAT
把下一个输入符号读进a中；
If S[k]∈ VT then j = k else j = k-1;
While S[j] > a do
Begin
Repeat
Q = S[j];
if S[j-1] VT then j = j-1 else j = j-2
until S[j] < Q;
把S[j+1]…S[k]归约为某个N，并输出归约为哪个符号；
K = j+1;
S[k] = N;
end of while
if S[j] < a or S[j] = a then
begin k = k+1; S[k] = a end
else error //调用出错诊察程序
until a = ‘#’

算法解释说明：a中存放的是目前分析到的句子中的终结符,不断比较栈顶的首终结符s[j]与a中的终结符的优先级。若s[j]优先级低于a或与a相同，则a中 终结符进栈；若s[j]优先级高于a， 则在栈中向下找，直到找到优先级比s[j] 低的终结符，假设用b表示，然后将栈中b之上的串（就是最左素短语）归约到N（弹出栈中b之上的串，N入栈），此时栈顶首终结符b就是新的s[j]，接着比较栈顶首终结 符s[j]和a的优先级，重复以上步骤。

（4）算法流程图

四、源程序及调试运行结果

1.源程序代码：

#include 
#include //万能头文件
using namespace std;
#define M 9
// 算符优先关系表
int findP(int a, int b) // a、b ∈ [1,9]，从1开始
{
    int table[M][M] =  // 1表示优先级高于，-1表示优先级低于，0表示优先级等于，2表示空
    {
        {0,0,-1,-1,-1,-1,-1,1,1},
        {0,0,-1,-1,-1,-1,-1,1,1},
        {1,1,0,0,-1,-1,-1,1,1},
        {1,1,0,0,-1,-1,-1,1,1},
        {1,1,1,1,0,2,2,1,1},
        {1,1,1,1,2,0,2,1,1},
        {-1,-1,-1,-1,-1,-1,-1,0,1},
        {1,1,1,1,2,2,0,1,1},
        {-1,-1,-1,-1,-1,-1,-1,-1,0}
    };
    return table[a-1][b-1]; //数组下标从0开始
}
// 判断c是否终结符，不是返回0，是返回它在优先关系表中的行号（从1开始）
int Is_Vt(char c)
{
    int n;
    switch(c)
    {
    case 'p':
        n=1;
        break; //plus +
    case 'm':
        n=2;
        break;//minus -
    case 't':
        n=3;
        break;//times *
    case 's':
        n=4;
        Break;//slash /
    case 'i':
        n=5;
        break;//ident
    case 'n':
        n=6;
        break;//number
    case 'l':
        n=7;
        break;//lparen （
    case 'r':
        n=8;
        break;//rparen ）
    case '#':
        n=9;
        break;
    default:
        n=0;
    }
    return n;
}
void Getinputs(char* inputs)//输入
{
    int i = 0;
    string line;
    while(cin >> line)
    {
        inputs[i++] = line[1];
    }
    inputs[i] = '#';
}
// 判断表达式的合法性，p指向分析栈的首部，k指向栈顶；psc指向当前输入符号
int judge(char* p, int k, char* psc)
{
    //当前输入符号为运算符，而栈顶为#，运算符前面没有操作数
    if(k == 1 && p[k] == '#' && (*psc == 'p' || *psc == 'm' || *psc == 't' || *psc == 's'))
    {
        return 0;
    }  
 //当前输入符号为#，上一个输入符号为运算符，运算符后面没有操作数
    if(*psc == '#' && (*(psc-1) == 'p' || *(psc-1) == 'm' || *(psc-1) == 't' || *(psc-1) == 's'))
    {
        return 0;
    }
    //运算符号相邻
    if(((*psc == 'p' || *psc == 'm' || *psc == 't' || *psc == 's') && ((*(psc+1) == 'p' || *(psc+1) == 'm' || *(psc+1) == 't' || *(psc+1) == 's'))))
    {
        return 0;
    }
    return 1;
}
int main()
{
    char s[30] = {'\0'};//分析栈s
    int k = 1; // k指向栈顶
    s[k] = '#';
    s[k+1] = '\0';
    int j; // j指向栈顶的终结符
    char q; // q表示j指向的元素，即栈顶终结符
    // 输入处理
    char inputs[100] = {'\0'}; // 输入串
    Getinputs(inputs);
    //printf("字符串是：%s\n", inputs);
    char *psc = inputs; // 指向当前输入符号
    int flag; // 查算符优先关系表得到的值（1/-1/0/2）(大于/小于/等于/空)
    // 算符优先分析算法总控程序
    while(1)
    {
        if(!judge(s, k, psc)) //表达式不合法，直接报错
        {
            printf("No,it is wrong.");
            exit(1);
        }
        // 让j指向栈顶终结符
        if(Is_Vt(s[k]))
            j = k;
        else
            j = k-1;
   // 比较s[j]和*psc(当前输入符号）的优先关系，判断移进还是规约
        flag = findP(Is_Vt(s[j]), Is_Vt(*psc));
        if(flag == 1) // s[j] 优先级高于 *psc，进行规约
        {
            //在栈顶中向下找，直到找到优先级低于s[j]的终结符
            do
            {
                q = s[j];// q保存当前的终结符
                // j向下探一（两）步，找到下一个终结符
                if(Is_Vt(s[j-1]))
                    j--;
                else
                    j-=2;
            }
            while(findP(Is_Vt(s[j]), Is_Vt(q)) != -1);
            k = j+1;
            s[k] = 'N'; // 将栈中q以上（不包括q)的串归约到N
            s[k+1] = '\0';
            continue;
        }
        else if(flag == -1)  // s[j] 优先级低于*psc，移进
        {
            k++;
            s[k] = *psc;
            s[k+1] = '\0';
            psc++;
            continue;
        }
        else if(flag == 0)
        {
            if(s[j] == '#')
            {
                printf("Yes,it is correct.");
                break;
            }
            else // 否则移进
            {
                k++;
                s[k] = *psc;
                s[k+1] = '\0';
                psc++;
                continue;
            }
        }
        else // 优先关系表中为空的地方
        {
            printf("No,it is wrong.");
            exit(1);
        }
    }
    return 0;
}

2.程序运行结果截图
测试数据一：

测试数据二：