Levenshtein莱文斯坦计算相似度距离
https://github.com/ztane/python-Levenshtein/
https://pypi.org/project/python-Levenshtein/
Levenshtein.distance(str1,str2)
1.百度百科介绍:
Levenshtein 距离,又称编辑距离,指的是两个字符串之间,由一个转换成另一个所需的最少编辑操作次数。
许可的编辑操作包括将一个字符替换成另一个字符,插入一个字符,删除一个字符。
编辑距离的算法是首先由俄国科学家Levenshtein提出的,故又叫Levenshtein Distance。
2.用途
模糊查询
3.实现过程
a.首先是有两个字符串,这里写一个简单的 abc和abe
b.将字符串想象成下面的结构。
A处 是一个标记,为了方便讲解,不是这个表的内容。
| abc | a | b | c | |
| abe | 0 | 1 | 2 | 3 |
| a | 1 | A处 | ||
| b | 2 | |||
| e | 3 |
c.来计算A处 出得值
它的值取决于:左边的1、上边的1、左上角的0.
按照Levenshtein distance的意思:
上面的值和左面的值都要求加1,这样得到1+1=2。
A处 由于是两个a相同,左上角的值加0.这样得到0+0=0。
这是后有三个值,左边的计算后为2,上边的计算后为2,左上角的计算为0,所以A处 取他们里面最小的0.
d.于是表成为下面的样子
| abc | a | b | c | |
| abe | 0 | 1 | 2 | 3 |
| a | 1 | 0 | ||
| b | 2 | B处 | ||
| e | 3 |
在B处 会同样得到三个值,左边计算后为3,上边计算后为1,在B处 由于对应的字符为a、b,不相等,所以左上角应该在当前值的基础上加1,这样得到1+1=2,在(3,1,2)中选出最小的为B处的值。
e.于是表就更新了
| abc | a | b | c | |
| abe | 0 | 1 | 2 | 3 |
| a | 1 | 0 | ||
| b | 2 | 1 | ||
| e | 3 | C处 |
C处 计算后:上面的值为2,左边的值为4,左上角的:a和e不相同,所以加1,即2+1,左上角的为3。
在(2,4,3)中取最小的为C处 的值。
f.于是依次推得到
| a | b | c | ||
| 0 | 1 | 2 | 3 | |
| a | 1 | A处 0 | D处 1 | G处 2 |
| b | 2 | B处 1 | E处 0 | H处 1 |
| e | 3 | C处 2 | F处 1 | I处 1 |
I处: 表示abc 和abe 有1个需要编辑的操作。这个是需要计算出来的。
同时,也获得一些额外的信息。
A处: 表示a 和a 需要有0个操作。字符串一样
B处: 表示ab 和a 需要有1个操作。
C处: 表示abe 和a 需要有2个操作。
D处: 表示a 和ab 需要有1个操作。
E处: 表示ab 和ab 需要有0个操作。字符串一样
F处: 表示abe 和ab 需要有1个操作。
G处: 表示a 和abc 需要有2个操作。
H处: 表示ab 和abc 需要有1个操作。
I处: 表示abe 和abc 需要有1个操作。
g.计算相似度
先取两个字符串长度的最大值maxLen,用1-(需要操作数除maxLen),得到相似度。
例如abc 和abe 一个操作,长度为3,所以相似度为1-1/3=0.666。
4.代码实现
package code;
/**
* @className:MyLevenshtein.java
* @classDescription:Levenshtein Distance 算法实现
* 可以使用的地方:DNA分析 拼字检查 语音辨识 抄袭侦测
* @author:donghai.wan
* @createTime:2012-1-12
*/
public class MyLevenshtein {
public static void main(String[] args) {
//要比较的两个字符串
String str1 = "今天星期四";
String str2 = "今天是星期五";
levenshtein(str1,str2);
}
/**
* DNA分析 拼字检查 语音辨识 抄袭侦测
*
* @createTime 2012-1-12
*/
public static void levenshtein(String str1,String str2) {
//计算两个字符串的长度。
int len1 = str1.length();
int len2 = str2.length();
//建立上面说的数组,比字符长度大一个空间
int[][] dif = new int[len1 + 1][len2 + 1];
//赋初值,步骤B。
for (int a = 0; a <= len1; a++) {
dif[a][0] = a;
}
for (int a = 0; a <= len2; a++) {
dif[0][a] = a;
}
//计算两个字符是否一样,计算左上的值
int temp;
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
temp = 0;
} else {
temp = 1;
}
//取三个值中最小的
dif[i][j] = min(dif[i - 1][j - 1] + temp, dif[i][j - 1] + 1,
dif[i - 1][j] + 1);
}
}
System.out.println("字符串\""+str1+"\"与\""+str2+"\"的比较");
//取数组右下角的值,同样不同位置代表不同字符串的比较
System.out.println("差异步骤:"+dif[len1][len2]);
//计算相似度
float similarity =1 - (float) dif[len1][len2] / Math.max(str1.length(), str2.length());
System.out.println("相似度:"+similarity);
}
//得到最小值
private static int min(int... is) {
int min = Integer.MAX_VALUE;
for (int i : is) {
if (min > i) {
min = i;
}
}
return min;
}
}
1. Levenshtein.hamming(str1, str2)
计算汉明距离。要求str1和str2必须长度一致。是描述两个等长字串之间对应位置上不同字符的个数。如
2. Levenshtein.distance(str1, str2)
计算编辑距离(也成Levenshtein距离)。是描述由一个字串转化成另一个字串最少的操作次数,在其中的操作包括插入、删除、替换。如
算法实现 参考动态规划整理:http://www.cnblogs.com/kaituorensheng/archive/2013/05/15/3080990.html。
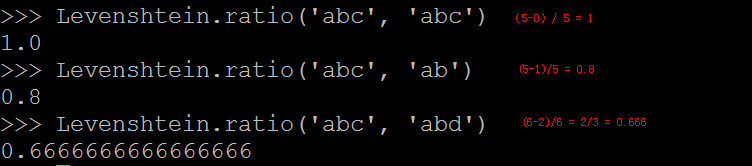
3. Levenshtein.ratio(str1, str2)
计算莱文斯坦比。计算公式 r = (sum - ldist) / sum, 其中sum是指str1 和 str2 字串的长度总和,ldist是类编辑距离
注意:这里的类编辑距离不是2中所说的编辑距离,2中三种操作中每个操作+1,而在此处,删除、插入依然+1,但是替换+2
这样设计的目的:ratio('a', 'c'),sum=2,按2中计算为(2-1)/2 = 0.5,’a','c'没有重合,显然不合算,但是替换操作+2,就可以解决这个问题。
4. Levenshtein.jaro(s1, s2)
计算jaro距离,
其中的m为s1, s2的匹配长度,当某位置的认为匹配 当该位置字符相同,或者在不超过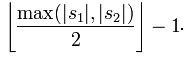
t是调换次数的一半
5. Levenshtein.jaro_winkler(s1, s2)
计算Jaro–Winkler距离![]()