2024牛客寒假算法基础集训营1
团购50块,一共6场。感觉难度比较适合,题型和cf上面不太一样,还挺新颖,比较有意思。解法很多,提供一下我自己的解法。题目顺序按我感觉的难度来排。顺序:AMLGEBC IHF KDJ
比赛链接
出题人B站直播视频讲解录播1,出题人B站直播视频讲解录播2 我个人觉得讲的是一坨
A DFS搜索
思路:
可以真的dfs爆搜,出题人考虑到有的萌新真的会上当所以数据范围给的爆搜也能过。
也可以这样搞:用个变量x记录一下匹配好了几个字符,遍历每个位置,如果x=0并且碰到了字符D,就x++,如果x=1并且碰到了字符F,就再++,如果x=2并且碰到了字符S,就再++。最后看一下x能不能统计到3就行了。同理dfs。
code:
#include M 牛客老粉才知道的秘密
思路:
相当于 紧贴左边向右滑动 和 紧贴右边向左滑动 两种情况之和,如果n能被6整除,两种情况是重合的,否则两种情况都算。
code:
#include L 要有光
思路:
感觉很简单啊为啥过的这么少。都被立体几何吓到了?
假设光源在某一个点,看看咋投影的:
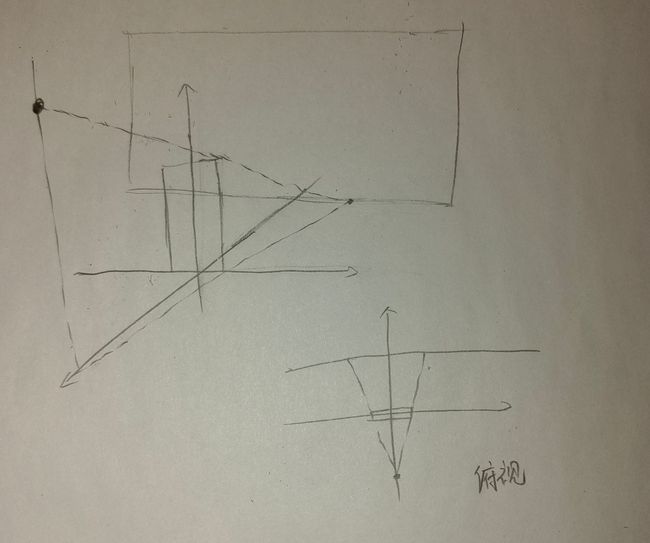
向上动会导致有的地面盖不到,向下动的话,覆盖范围也没有变,所以答案就是俯视图中梯形的面积,用相似三角形推一下边的长度关系可以算出来梯形面积为 3 c w 3cw 3cw。
code:
#include G why买外卖
思路:
判断一个优惠券能否使用看的是原价,如果原价确定了,能用的优惠券就确定了,肯定贪心地用掉所有能用的优惠券。这样实际要花的钱就确定了。
所以直接二分答案,检查这个答案合不合法即可。
另外一种方法:因为需要原价更高才能使用的优惠券使用时,需要原价低的优惠券一定能用,所以按需求原价排序,处理优惠钱数的前缀和,然后枚举每个 i i i,看看使用前 i i i 个优惠券需要的钱是否够用,够用的话,看看使用前 i i i 个优惠券可以买到的最大价格的烧鸡,存储最大值即可。
code:
#include E 本题又主要考察了贪心
思路:
诈骗题,出题人都是大猪蹄子。
一开始考虑贪心,但是发现找不到正确的贪心策略。首先有1的对局肯定1赢,如果贪心地让分数最少的对手赢的话,那么2 1 1,最后两人比一场怎么办?如果贪心地让所有人平局,那么3 3 0,最后两人比一场怎么办?反例太好找了。
看一眼数据范围,比赛数量太少了,少的可疑,遂直接放弃思考选择暴力dfs(实际上正解就是暴力,题目诈骗)
其实每场比赛就三种结果,一方赢了,另一方赢了,平局。所以还可以使用三进制压缩,用一个十位三进制数就可以说明所有比赛的结果了。
code:
#include B 关鸡
思路:
想法很多,但是都不好写。我考虑了很多种想法但是感觉都容易写出锅,所以直接写一串if枚举所有情况了。
看看左右两边(准确来说,是横坐标 [ 0 , ± ∞ ) [0,\pm\infty) [0,±∞) )出现什么情况可以堵死。首先是如果有两个点,横坐标差1或0,纵坐标不同,它就可以堵死一个方向。如果只有一个单个点,就可以在它上/下面放一把火,就堵死了。入果一个方向上一把火都没有,那就得放两把火。一般来说是这样。
但是发现横坐标为0,纵坐标为1的时候,这把火可以被两个方向共用,如果 ( 2 , 0 ) (2,0) (2,0) 有一把火,那么最多就在 ( 1 , 1 ) (1,1) (1,1) ( 1 , − 1 ) (1,-1) (1,−1) 放两把火就可以把两条路都堵死了。
所以设置7个bool变量,记录左边有没有堵死,有没有火,右边有没有堵死,有没有火, ( 2 , 0 ) (2,0) (2,0) ( 1 , 1 ) (1,1) (1,1) ( 1 , − 1 ) (1,-1) (1,−1) 这三个点有没有火。然后枚举情况:
- 左右都堵死了:答案为0
- 左右有一边堵死:
- 另一边有火:点一把火堵死
- 另一边没火:点两把火堵死
- 两边都没堵死:
- 两边都有火:
- ( 1 , 1 ) (1,1) (1,1) ( 1 , − 1 ) (1,-1) (1,−1)都有火:点一把火,在 ( 2 , 0 ) (2,0) (2,0)
- 点两把火
- 一边有火:
- ( 1 , 1 ) (1,1) (1,1) ( 1 , − 1 ) (1,-1) (1,−1)某一个位置有火( ( 2 , 0 ) (2,0) (2,0) 在中间,如果它本来有火,那么记录的应该两边都有火,所以这里一定不会有火):点两把火, ( 1 , 1 ) (1,1) (1,1) ( 1 , − 1 ) (1,-1) (1,−1) ( 2 , 0 ) (2,0) (2,0) 都有火
- 点三把火,在 ( 1 , 1 ) (1,1) (1,1) ( 1 , − 1 ) (1,-1) (1,−1) ( 2 , 0 ) (2,0) (2,0)
- 没火:
- 点三把火,在 ( 1 , 1 ) (1,1) (1,1) ( 1 , − 1 ) (1,-1) (1,−1) ( 2 , 0 ) (2,0) (2,0)
- 两边都有火:
然后就没了。
code:
#include C 按闹分配
思路:
排队接水,如果没有鸡插队的话,要保证总接水时间最短,就是一个简单贪心。按接水时间从小到大排序,这样接水的序列就确定了,假设 ∑ k = i j D k \sum_{k=i}^j D_{k} ∑k=ijDk 写成 D i ∼ j D_{i\sim j} Di∼j。如果把鸡插在第 i i i 个人后面,等待的总时间就变成了 S c = D 1 ∼ i + D i + 1 ∼ n + ( n − i ) ∗ t c (后面 n − i 个人每人多等 t c 时间) S_{c}=D_{1\sim i} +D_{i+1\sim n}+(n-i)*t_c\quad\text{(后面 $n-i$ 个人每人多等 $t_c$时间)} Sc=D1∼i+Di+1∼n+(n−i)∗tc(后面 n−i 个人每人多等 tc时间) = D 1 ∼ n + ( n − i ) ∗ t c = S m i n + ( n − i ) ∗ t c =D_{1\sim n} +(n-i)*t_c=S_{min}+(n-i)*t_c =D1∼n+(n−i)∗tc=Smin+(n−i)∗tc根据题目上 S c − S m i n ≤ M S_{c}-S_{min}\le M Sc−Smin≤M,得到: ( n − i ) ∗ t c ≤ M (n-i)*t_c\le M (n−i)∗tc≤M i ≥ n − M t c i\ge n- \dfrac M {t_c} i≥n−tcM由于 i i i 取最小整数,因此 i = ⌈ n − M t c ⌉ = n − ⌊ M t c ⌋ i=\left\lceil n- \dfrac M {t_c}\right\rceil=n- \left\lfloor\dfrac M {t_c}\right\rfloor i=⌈n−tcM⌉=n−⌊tcM⌋这时鸡的等待时间就是 ∑ k = 1 i t k + t c \sum_{k=1}^it_k+t_c ∑k=1itk+tc,前缀和处理前面那个就行了。
其实还想过加入鸡后 排好顺序后的人之间能不能换位置,但是题目好像没说可以,那就不考虑,那就简单了。
code:
#include I It’s bertrand paradox. Again!
思路1:
这题很神秘,就是很多做法其实都可以,因为两个人生成数据的方法不同,会导致有的数据会呈现一定规律,比如第一个人bit-noob生成的xy就会非常随机,出现在任何位置都有可能,但是r就会偏小(因为有的不满足的大r被重新生成为了小r)。而第二个人buaa-noob生成的xyr就会不那么随机。
所以核心思想就是:找到两种方法会使得哪个统计量有显著区别,尝试区分这个统计量的均值。
我是直接把两种生成数据的方法都真的敲出来,然后查看半径r的中位数,发现第一个人的r的中位数在11左右,而第二个的在20左右。那么我们对输入的r排一下序,然后看中位数大于还是小于15就行了。
code1:
#include
//
// for(int i=1,x,y,r,maxx;i<=n;i++){
// do{
// x=rand()%201-100;
// y=rand()%201-100;
// r=rand()%101;
// maxx=1e9;
// maxx=min(min(min(100-x,x+100),min(100-y,y+100)),maxx);
// }while(r>maxx);
// a[i]=r;
// }
// sort(a+1,a+n+1);
// cout<
cin>>n;
for(int i=1,x,y,r;i<=n;i++){
cin>>x>>y>>r;
a[i]=r;
}
sort(a+1,a+n+1);
if(a[n/2]<=15)puts("bit-noob");
else puts("buaa-noob");
return 0;
}
思路2:
题解是考虑圆心坐标在 { ( x , y ) ∣ − 70 ≤ x ≤ 70 , − 70 ≤ y ≤ 70 } \{(x,y)|-70\le x\le70,-70\le y\le70\} {(x,y)∣−70≤x≤70,−70≤y≤70} 区域的点的个数。显然横坐标本来的范围是 ( − 100 , 100 ) (-100,100) (−100,100) 共199个取值,范围内共141个取值(别忘了零点),同理纵坐标,所以一个点落在上述区域内的概率是 p = 141 ∗ 141 199 ∗ 199 p=\dfrac{141*141}{199*199} p=199∗199141∗141,一共 1 0 5 10^5 105 个点,均值也就是说大概会有 p ∗ 1 0 5 p*10^5 p∗105个点落在范围内,其实大概就是50000多个点。
一个点要么落在范围内,概率为 p p p,要么落在范围外,概率为 1 − p 1-p 1−p。概率论学的比较好的话可以比较敏锐地看出这是个二项分布,即一共 n = 1 0 5 n=10^5 n=105 个点,假设落在范围内的点的个数为 X X X,则有 X ∼ B ( n = 1 0 5 , p = 141 ∗ 141 199 ∗ 199 ) X\sim B(n=10^5,p=\dfrac{141*141}{199*199}) X∼B(n=105,p=199∗199141∗141),所以 X X X 满足正态分布 X ∼ N ( μ = n p , σ 2 = n p ( 1 − p ) ) X\sim N(\mu=np,\sigma^2=np(1-p)) X∼N(μ=np,σ2=np(1−p)),可以用计算器算出 p ≈ 0.502 , μ = n p ≈ 50203 , σ = n p ( 1 − p ) ) ≈ 25000 ≈ 158 p\approx0.502,\mu=np\approx50203 ,\sigma=\sqrt{np(1-p))}\approx \sqrt{25000}\approx 158 p≈0.502,μ=np≈50203,σ=np(1−p))≈25000≈158。
查表可知,正态分布分布在 μ − 3 σ ≤ X ≤ μ + 3 σ \mu-3\sigma \le X \le \mu+3\sigma μ−3σ≤X≤μ+3σ 范围的可能性在 0.9973 0.9973 0.9973 以上。在这个题里也就是说落在范围内的点的个数 X X X 在 ∣ X − μ ∣ = ∣ X − 50203 ∣ ≤ 3 σ = 474 |X-\mu|=|X-50203| \le 3\sigma=474 ∣X−μ∣=∣X−50203∣≤3σ=474 的概率在 99.73 % 99.73\% 99.73% 以上。所以可以近似看成如果 ∣ X − 50203 ∣ ≤ 474 |X-50203| \le 474 ∣X−50203∣≤474,那么这个数据就是第一个人bit-noob生成的。
正解写法(正解可能是不想算 σ \sigma σ 到底是啥了,直接猜了个2000):
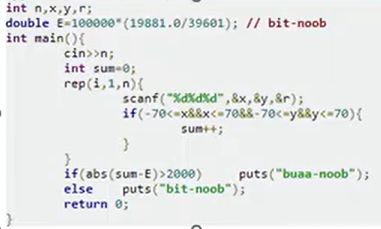
为啥会想到取 { ( x , y ) ∣ − 70 ≤ x ≤ 70 , − 70 ≤ y ≤ 70 } \{(x,y)|-70\le x\le70,-70\le y\le70\} {(x,y)∣−70≤x≤70,−70≤y≤70} 范围(我猜的):因为 141 ∗ 141 199 ∗ 199 \dfrac{141*141}{199*199} 199∗199141∗141 正好约等于 1 2 \dfrac 1 2 21。
code2:
#include H 01背包,但是bit
思路:
看着像背包,实际上是贪心。
考虑最后答案怎么样才能不超过 m m m,如果我们把 m m m 看成二进制数,最高位改成0,那么低位上所有的数都可以改成1,这意味着你可以拿所有二进制位是这个数子集的重量,直接贪心拿完。如果最高位不动,把次高位改成0,那么次高位的低位都可以改成1,可以拿所有二进制位是这个数子集的重量,类推。所以我们只需要枚举 m m m 所有二级制上的1,然后像样计算此时的答案,记录最大值即可。注意什么都不改的情况也成立,这个情况也算一下。
code:
#include F 鸡数题!
思路:
这个其实考的第二类斯特林数,会,看出来是,这个题就没什么意思。不会也能推出来,容斥定理。
为啥是斯特林数,其实这几个限制条件的意思就是把 2 n − 1 2^n-1 2n−1 二进制上的 n n n 个 1 1 1 分成 m m m 份(分好之后排序,就是一个满足条件的序列了。m个相同的组意味着唯一,排好序也是唯一,唯一对唯一,情况是一一对应的),每份不能为空,问你有多少种分法。
容斥定理推理:n个不同的物品分给m个相同的组,每组不能为空。
考虑每组可以为空,组组之间不同的情况,这时候每个物品有m个选择,一共是 m n m^n mn 种可能。
考虑有一组一定为空,其他组可以为空,组组之间不同的情况,这时候先选择一个组,这时候每个物品有m-1个选择,一共是 C m 1 ∗ ( m − 1 ) n C_m^1 * (m-1)^{n} Cm1∗(m−1)n 种可能。
同理,有两组一定为空的情况,一共是 C m 2 ∗ ( m − 2 ) n C_m^2 * (m-2)^{n} Cm2∗(m−2)n 种可能,后面的情况递推。
根据容斥定理,n个不同的物品分给m个不同的组,每组不能为空的情况一共是: C m 0 ∗ m n − C m 1 ∗ ( m − 1 ) n + C m 2 ∗ ( m − 2 ) n − ⋯ + ( − 1 ) k ∗ C m k ∗ ( m − k ) n + ⋯ + ( − 1 ) m ∗ C m m ∗ 0 n = ∑ i = 0 m ( − 1 ) i ∗ C m i ∗ ( m − i ) n C_m^0*m^n-C_m^1 * (m-1)^{n}+C_m^2 * (m-2)^{n}-\dots+(-1)^k*C_{m}^k * (m-k)^{n}\\+\dots+(-1)^m*C_{m}^m * 0^{n}=\sum_{i=0}^m(-1)^i*C_{m}^i * (m-i)^{n} Cm0∗mn−Cm1∗(m−1)n+Cm2∗(m−2)n−⋯+(−1)k∗Cmk∗(m−k)n+⋯+(−1)m∗Cmm∗0n=i=0∑m(−1)i∗Cmi∗(m−i)n
因为是不同的,如果是相同的组,不同的组会比它多乘一个全排列情况,也就是 m ! m! m!,除以它就是n个不同的物品分给m个相同的组,每组不能为空的情况数了。即: 1 m ! ∑ i = 0 m ( − 1 ) i ∗ C m i ∗ ( m − i ) n \dfrac 1 {m!}\sum_{i=0}^m(-1)^i*C_{m}^i * (m-i)^{n} m!1i=0∑m(−1)i∗Cmi∗(m−i)n = ∑ i = 0 m 1 m ! ( − 1 ) i ∗ m ! i ! ∗ ( m − i ) ! ∗ ( m − i ) n =\sum_{i=0}^m \dfrac {1} {m!} (-1)^i*\dfrac {m!} {i!*(m-i)!} * (m-i)^{n} =i=0∑mm!1(−1)i∗i!∗(m−i)!m!∗(m−i)n = ∑ i = 0 m ( − 1 ) i ∗ ( m − i ) n i ! ∗ ( m − i ) ! =\sum_{i=0}^m \dfrac {(-1)^i*(m-i)^{n}} {i!*(m-i)!} =i=0∑mi!∗(m−i)!(−1)i∗(m−i)n
预处理一下阶乘,然后递推累加即可。
code:
#include K 牛镇公务员考试
思路:
题面看起来不太好理解。就是第 i i i 个点到点 a i a_i ai 有一条单向边,当点 i i i 取字符 A ∼ E A\sim E A∼E 其中一个时,点 a i a_i ai 取后面的字符串中相应的字符,也就是说,A对应s[1],B对应s[2],C对应s[3],D对应s[4],E对应s[5]。
单说n个点n条边,每个点只有一个出边。这是一个内向基环树(当然也可能是基环树森林)。如果一个基环树的环上某个点取一个选项,那么它下一个点的选项也就确定了,同理整个环上的点都确定了选项,环上连着的树也都确定了选项。所以我们只需要随便取一个基环树上的点,假设它选择五个选项中的一个,看是否能成立,数一下这个基环树能产生几种可能的解,所有解的个数相乘即可。
如何判断成立:一个点的选项确定了,那么它的上一个点和下一个点的选项也都确定了,不会出现问题。问题出现在环上最后一个没有确定的点确定后,它还要满足 它下一个那个确定了的点的选项 和 它确定的下一个点的选项 要一致,一致的话就会产生一个可行的答案。
可以看到其实环上连的树时没有什么作用的,我们只要看环就可以了,环确定了,树也就确定了。所以可以直接无视。
code:
#include D 数组成鸡
思路:
参考了jiangly大佬和题解的做法。不知道哪里写的有问题,改吐了。这题很多做法都可以过,核心是要注意到:询问的M范围不大,所以数组稍微长一点儿,就很可能溢出 1 0 9 10^9 109 的范围,所以要考虑的方案其实很少。
先统计好每一个数和它的个数,可以直接用map来统计。考虑到其实如果有很多数是不一样的,那么即使把一些数变成了1或-1,无论怎么搞其他数乘起来还是会超过 1 0 9 10^9 109 。可以算出来大概 ( 8 ! ) 2 (8!)^2 (8!)2 就会超,也就是如果有16个不同的数,它们的乘积一定会会超过 1 0 9 10^9 109,直接就可以全部输出no了,不过这里有一个例外,0的话是可以凑出来的,这个数要特判。
现在就剩下16个不同的数了。全体加减一个数,结果快速幂累乘起来很快,一次计算最多也就是大常数log次(实际上快速幂乘到超出 1 0 9 10^9 109 时可以直接返回一个很大的数,大概率log都跑不满)。考虑如何乘出M。
考虑M可以分解成几个数的乘积(不是质因数,可以有正有负),如果改变后的数组恰好是这几个因数(可以有正有负)以及若干个1以及-1,那就凑出来了。因为数组中一个数确定了,其他的数也都随之确定了,那必然数组中有一个数变化后是M的一个因数,因为数组大小至少为2,那么M至少有一个因数绝对值是在 1 0 9 ≈ 3.2 ∗ 1 0 4 \sqrt{10^9}\approx 3.2*10^4 109≈3.2∗104 以内的。所以我们枚举数组中每一个数变化成绝对值为 1 0 9 \sqrt{10^9} 109 某个数时数组的乘积,就可以包含到所有可以凑出来的M。之后询问的时候直接查询即可。最坏时间复杂度是 O ( 16 l o g ∗ 1 0 9 ) O(16log*\sqrt{10^9}) O(16log∗109)。
这里题解有一个想法可以进行一步优化:因为数组要么最大值绝对值在 1 0 9 \sqrt{10^9} 109 内,要么次大值绝对值在 1 0 9 \sqrt{10^9} 109 内,否则,这两个数乘积的绝对值一定大于 1 0 9 10^9 109。两个数都是M的因子,而且两个之中一定有一个绝对值 ≤ 1 0 9 \le \sqrt{10^9} ≤109,因此只枚举这两个数绝对值等于 1 0 9 \sqrt{10^9} 109 内某个数,就可以包含到M了,不需要全都枚举一遍。
code:
#include J 又鸟之亦心
思路1:
说一下jiangly大佬的 O ( n l o g 2 n ) O(nlog^2n) O(nlog2n) 做法和某个大佬 O ( n l o g n ) O(nlogn) O(nlogn) 的做法。本着优先队列的思想,先说 O ( n l o g 2 n ) O(nlog^2n) O(nlog2n) 的。
因为如果距离最大值 小的可以成立,那么大的一定成立,考虑二分答案。对一个答案,考虑如何分配两人。
先想象一下这两人是怎么走的,应该是一个人走一连串的点,另一个人留在原地。然后这个人停在这一串点的最后一个点上,另一个人走下一串连续的点,以此类推,所以说,一个人如果想要一直停在一个点上,另一个人就要走完后面的所有点,可以这样做的前提就是后面所有点到这个点的距离小于等于答案。
那么当一个人走到点 a i a_i ai,另一个人有可能在前面的什么位置?就是所有满足 可能的这个位置到后面所有点一直到 a i a_i ai 这个点的距离都小于等于答案 的位置。只要满足,一个人可以停在任意一个这个可能在的位置,然后另一个人走完后面一串的点到 a i a_i ai。
我们设置一个集合set,存储一个人走到 a i a_i ai,另一个人可能出现的所有位置,从 a 1 a_1 a1 到 a n a_n an 递推。
而当一个人要走向 a i a_{i} ai 时,因为集合内的所有位置已经验证好了 可能的位置 到 a i − 1 a_{i-1} ai−1 之间所有点的距离都小于等于答案,所以一个人走到 a i − 1 a_{i-1} ai−1 另一个人可能在的所有位置再验证一下到 a i a_{i} ai 的距离小于等于答案,就得到了一个人走到 a i a_{i} ai 另一个人可能在的所有位置。如果验证完了发现没有可能的位置,说明无解,否则一直到走到 a n a_{n} an,说明有办法在不超过答案的前提下走到所有点。
如果一个人走到 a i a_{i} ai 是可以成立的,那么这个位置就可以是新的可能出现的位置。插入set。
code1:
#include 思路2:
O ( n l o g n ) O(nlogn) O(nlogn)做法。思路和上面一致,不过不再使用set来存储可能出现的位置。而是直接贪心。
从后往前看,如果一个人走了一串点最终到达了 a i a_i ai,贪心地向前寻找第一个位置 j j j,使得满足 j + 1 j+1 j+1 到 i i i 的所有点到 j j j 的距离都小于等于答案,让另一个人停留在这里,同理,这个另一个人再向前推。
为什么这么贪心一定是对的:使用mx记录 j + 1 j+1 j+1 到 i i i 位置最大的点,mi记录位置最小的点,其实就是需要点 j j j 正好既在 [ m x − d , m x + d ] [mx-d,mx+d] [mx−d,mx+d] 范围里,又在 [ m i − d , m i + d ] [mi-d,mi+d] [mi−d,mi+d] 范围里,其实就是在 [ m x − d , m i + d ] [mx-d,mi+d] [mx−d,mi+d] 范围内。如果点 j j j 坐标在这个范围里面,另一个人停留在这里会使得mx和mi重新赋值为 a j a_j aj,换句话说,逆推的时候范围从 [ m x − d , m i + d ] [mx-d,mi+d] [mx−d,mi+d] 扩大到了 [ a j − d , a j + d ] [a_j-d,a_j+d] [aj−d,aj+d],范围扩大了当然是好事。如果不让另一个人停在这里,那么逆推的时候需要在的范围就会越来越苛刻。所以让另一个人停在这里一定比不让另一个人停在这里更好。因此这样贪心是对的。
不过这样逆推的话,起点也要放进序列里。不过顺序无所谓,因为答案一定大于等于两个人的起始位置之差。
code2:
#include 