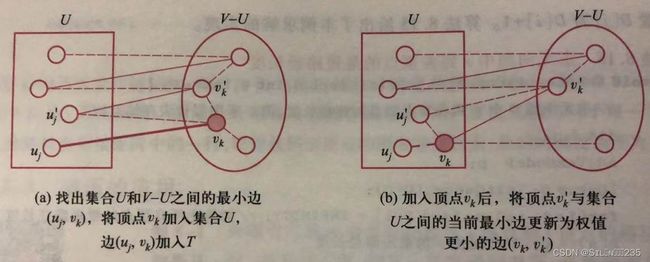
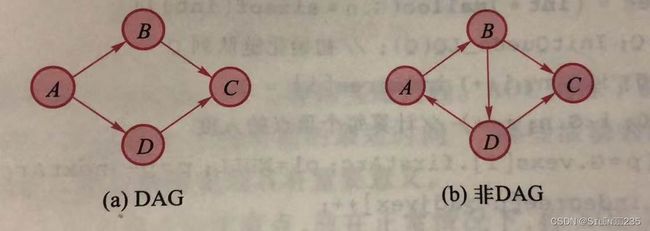
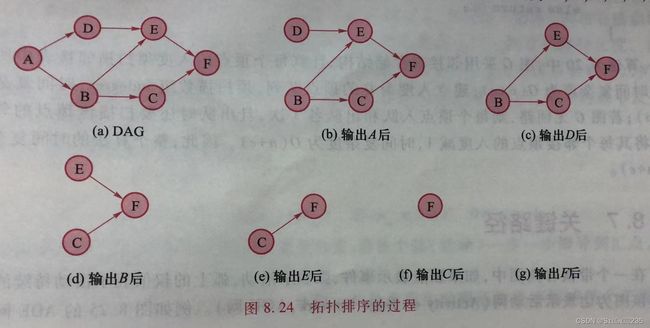
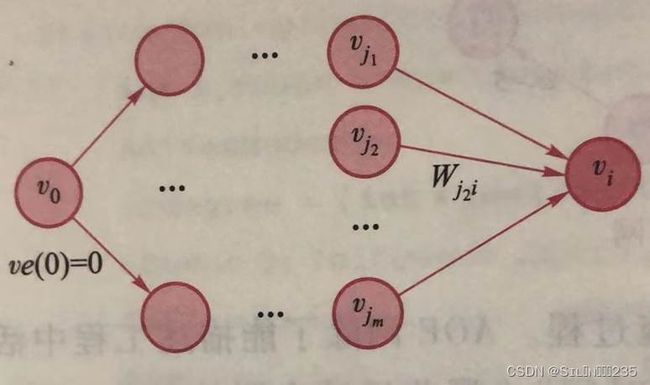
《数据结构》第八章:图
图是一种比树形结构更为复杂的非线性结构。在树形结构中,结点间有层次关系,每一层的一个结点能且只能和上一层的一个结点相关,但同时可以和下一层的多个结点相关,称为“多对多”关系。
8.1 图的基本概念
8.1.1 图的定义
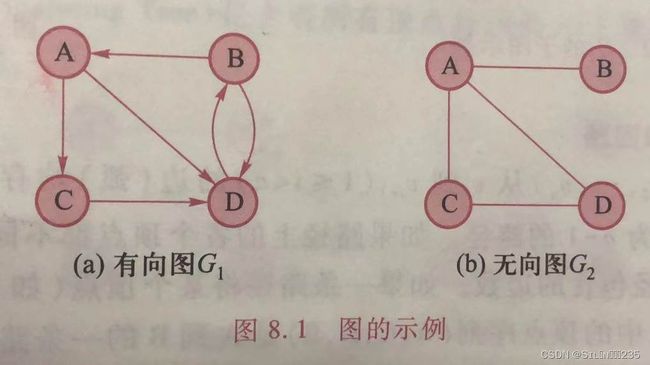
在图中,通常将数据元素称为顶点,顶点之间的关系称为边。图由有限顶点集V和有限边集E组成,记为
G=(V,E)
其中,顶点总数|V|记为n,边的总数|E|记为e。
8.1.2 图的术语
1.子图
假设两个图G=(V,E)和G’(V’,E’),如何V’ ⊆V且E’ ⊆E,则称G’为G的子图。
2.完全图
包含所有可能的边的图称为完全图。无向完全图包含n(n-1)/2条边,有向完全图包含n(n-1)条弧。
3.邻接顶点
有无向图,若存在边(v,w),则称v,w互为邻接顶点,或称v和w相邻接。
在有向图中,若存在弧
4.度、出度和入度
在图中,顶点的度是指依附于该顶点的边数。有向图顶点的度又分为出度和入度,出度是指以该顶点为起点的弧的数目,入度是指以该顶点为终点的弧的数目,顶点的度为出度和入度之和。
5.权和网
有时图中边或弧需要附加属性信息,比如表示两个顶点之间的距离、旅行时间或某种代价等,通常称此信息为权。带权的图称为带权图,或简称为网。
6.路径、简单路径和回路
如果顶点序列(v1,v2,…,vn)从vi到vi+1(1≤i≤n)的边(弧)均存在,则称顶点序列(v1,v2,…,vn)构成一条长度为n-1的路径。如果路径上的各个顶点都不同,则称这个路径为简单路径。路径长度是指路径博阿寒的边数。如果一条路径将某个顶点(如v1)连接到它自身,则称为回路。
7.连通图和强连通图
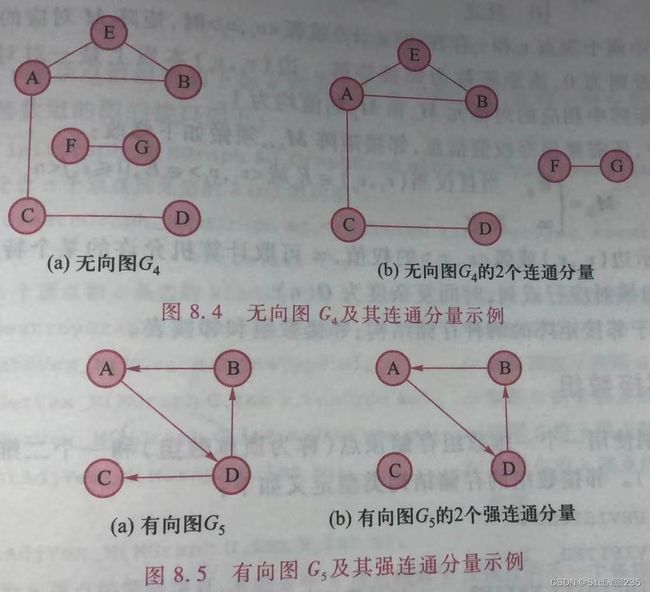
在无向图中,若顶点v到顶点w有路径,则称v和w是连通的。若图中任意两个顶点都是连通的,则称该图为连通图。连通分量是指无向图中的极大连通子图。
在有向图中,若图中任意两个顶点v和w,既有v到w的路径,又有w到v的路径,则称该图为强连通图。强连通分量是指有向图中的极大强连通子图。
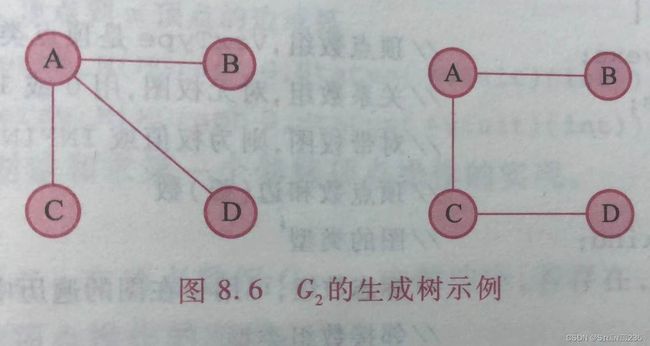
8.生成图
连通图的生成图是含有所有顶点且只有n-1条边的连通子图。
8.2 图的存储结构
图的任意两个顶点之间都可能存在边(弧)。在图的存储结构中,关键是如何表示边(弧)集。
假设图G=(V,E),顶点总数为n,边数为e。边(弧)集E的一种存储方法是用矩阵Mm×n表示:
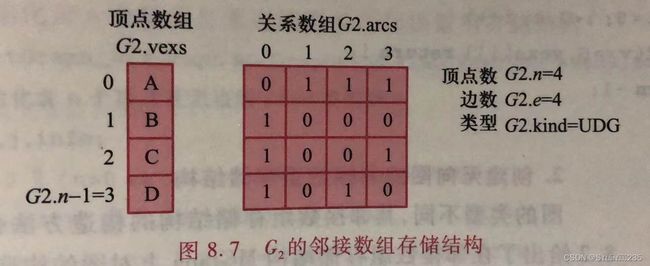
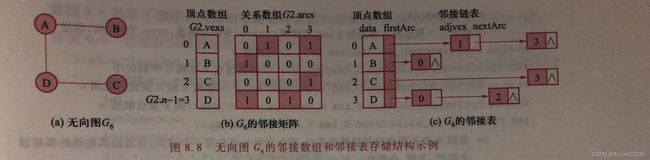
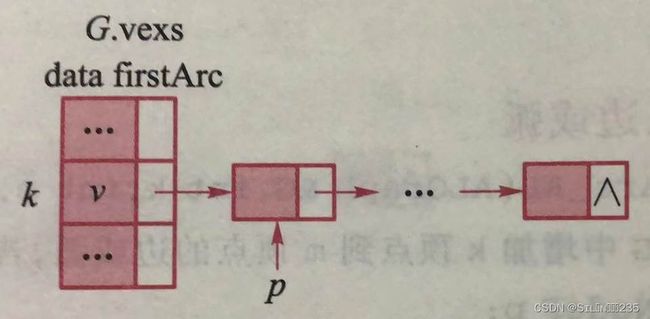
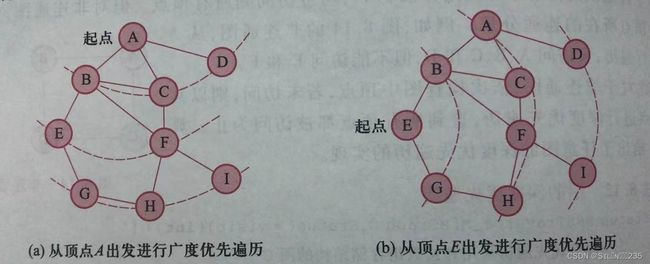
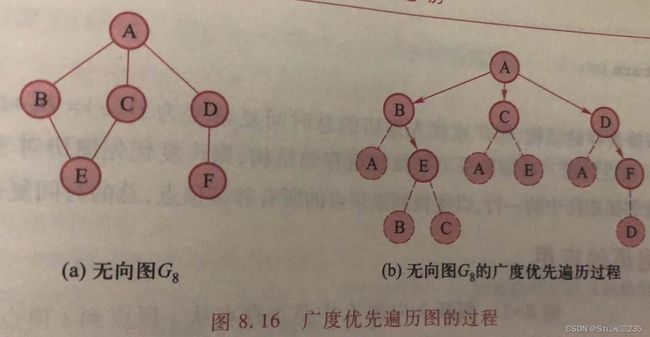
1 当且仅当(vi,vj)∈E或 M0={ 0 反之 其中,当图中两个顶点vi和vj存在边(vi,vj)或弧< vi,vj >时,矩阵M对应的第i行和第j列的元素值为1,否则为0,该矩阵称为邻接矩阵。边(vi,vj)本质上是一对对称弧 在带权图中,还需要保存权值信息,邻接矩阵Mn×n需做到如下修改: Wij 当且仅当(vi,vj)∈E或< vi,vj >∈E,0≤i,j<n Mij={ ∞ 反之 其中,Wij表示边(vi,vj)或< vi,vj >的权值,∞可取计算机允许的某个特定值。在该种方法中,查找边只需扫描对应的行或列,时间复杂度为O(n)。 邻接数组分别使用一个一维数组存储顶点(称为顶点数组)和一个二维数组存储邻接矩阵(称为关系矩阵)。邻接矩阵的存储结构类型定义如下: 采用邻接数组存储的无向图G2可定义如下: 图G的顶点v在顶点数组中的下标k称为称为v在G中的位序,也称v为G的第k顶点,简称k顶点。基于邻接数组的图的接口如下: 该操作查找图G的顶点v在顶点数组G。vexs中的位序,若存在,则返回其下标,否则返回-1. 算法:查找顶点 图的类型不同,其邻接数组存储结构的构造方法也不尽相同。 算法:创建图的邻接数组存储结构 无向图的创建过程如下: 算法:初始化含n个顶点且无边的图G的邻接数组存储结构 算法:创建无向图的邻接数组存储结构 图G中k顶点的第一个邻接顶点的位序是关系数组中第k行的第一个非零且非∞的元素的列号。 算法:求第一个邻接顶点 虽然采用邻接数组易于实现图的各种基本操作,但是,当图的边很少(即稀疏图)时,关系数组含有大量的0或者∞元素。为了节省存储空间,可采用邻接表存储结构,只存储非零或非∞元素。 图的邻接表由顶点数组和每个顶点的邻接链表组成。顶点数组元素除了含有存储顶点信息的data域外,还有指向其邻接链表的头指针firstArc域。每个顶点的邻接链表存储邻接顶点信息,链表的结点有3个域:adjvex存储邻接顶点的位序,nextArc是指向下一个结点的指针,info存储边(弧)的相关信息(如带权图的权值)。邻接链表中只存储了关系数组的非零元素信息,对于稀疏图,可有效节省存储空间。 邻接表存储结构的类型定义如下: 对于带权图,邻接链表中还需要存储权值信息(info域)。 基于邻接表的图的接口如下: 创建图的邻接表存储结构的操作CreateGraph_AL的实现与邻接数组相似。在CreateGraph_AL中调用的有向图的创建操作CreateDG_AL的过程如下: 算法:创建有向图的邻接表存储结构 对于弧 算法:插入边或弧 这个算法,需要判断边(弧)是否已经存在,因此需要遍历对应的邻接链表,其算法时间复杂度为O(e),但在邻接数组存储结构中,可直接判断无需查找,其算法时间复杂为O(1)。因此,若需频繁插入边(弧),宜采用邻接数组存储结构。 图G的k结点的第一个邻接顶点的位序存储在k结点的邻接链表的第一个结点。若结点存在,则令指针p指向它,并返回该结点存储的顶点位序,反之,则返回-1。 算法:求第一个邻接顶点 求k顶点的当前邻接顶点成功时,指针指向了邻接链表中环的相应结点。k顶点的下一个邻接顶点的位序就存储在p结点的下一个结点。 因此,若该结点存在,则令指针p指向它,并返回该结点存储的顶点位序,反之,返回-1. 算法:求下一个顶点位序 利用参数p使得求下一个邻接顶点操作的时间复杂度为O(1)。使用以上两个操作可一次访问k顶点的所有邻接顶点。算法时间复杂度为O(n)。 算法:求k顶点的所有邻接顶点 在实际应用中,经常需要基于顶点之间的关系依次访问图中的各个顶点。从概念上讲,图的遍历是对树的遍历的拓展。图的遍历从某一顶点出发,访问图中的所有顶点,且使每一顶点仅被访问一次。与树的遍历不同的是,图的遍历需要处理两种特殊情况:一是从某一顶点出发进行遍历时,可能访问不到所有其他顶点,比如非连通图;二是有些图存在回路,必须保证遍历过程不能因为回路陷入死循环中。 图的遍历时解决图的许多应用问题的基础,如路径问题、连通问题等。图的遍历有两种基本方法:深度优先遍历(深度优先搜索)和广度优先遍历(广度优先搜索) 类似于树的先序遍历,连通图的深度优先遍历的基本思路是,从图中指定顶点v出发,先访问该顶点;然后对v的所有邻接顶点wi依次检查,若wi未被访问,则以wi为新起点递归进行深度优先遍历。 为了能在递归过程中更好的判断顶点是否被访问过,需利用图G的标志数组G.tags,当访问i顶点时,将G.tags[i]值为VISITED。初始时所有顶点的标志值均为UNVISITED。 算法:连通图的深度优先遍历 对于连通图的任意顶点可以使用该算法均可访问到所有顶点。但对于非连通图,仅能访问到开始顶点所在的连通分量。 因此对于非连通图,依次检查图中所有顶点,若未访问,则以其为新起点进行深度优先遍历,直到所有顶点都被访问为止。 算法:图的深度优先遍历 如果采用邻接数组存储结构,在遍历中,需要扫描关系数组的对应行,才可以找到某个顶点的所有邻接存储结构,虽然邻接链表的结点共有2e个(无向图)或e个(有向图),但只需扫描e个结点即可完成遍历,加上访问n个头结点的时间,因此时间复杂度为O(n+e)。 类似于树的层次遍历,连通图的广度优先遍历的基本思想是,从图中指定顶点v出发,先访问该顶点;再依次访问v的所有未被访问的邻接顶点;然后再按之前邻接顶点被访问的先后次序依次访问它们的未被访问的邻接顶点;依次类推,直到所有从v可达的顶点被访问为止。 在实现广度优先遍历时,为保证能按顶点访问的顺序依次访问它们的未被访问的邻接顶点,需要借助队列,并利用标志数组判断顶点是否被访问过。广度优先遍历表述: 算法:图的广度优先遍历 如果采用邻接表存储结构,则广度优先遍历的总时间复杂度为O(e)=D1+ D2+ D3+…+ Di+…+ Dn-1,其中Di是i顶点的度。而如果采用邻接数组存储结构,则广度优先遍历对于每一个被访问的顶点,都要检查邻接矩阵中的每一行,以便找到该顶点的所有邻接顶点,总的时间复杂度为O(n2)。 例:判断有向图G中是否存在从是顶点到t顶点的路径。 如果从s到t的路径存在,则从s出发开始遍历。必能搜素到t,且一旦访问到t,遍历终止。此问题采用深度优先搜素和广度优先遍历均可。 算法:判断有向图中是否存在从s到t的路径 例:求无向图G中顶点s到其他顶点的最短路径长度 最短路径是指经过边数最少的路径。广度优先遍历访问过程正是按路劲长度递增次序依次访问所有可达到的顶点,因此,可基于广度优先遍历求解。 可引入一维数组D,D[i]存储s顶点到i顶点的最短路径长度,D[s]=0.在广度优先遍历中,当访问i顶点的未访问的邻接顶点j时,则置D[j]为D[i]+1。 算法:求无向图中s到各顶点的最短路径长度 在n个城市之间架设通信网络,如何实现成本最小化?显然可用连通带权图G建模,其中顶点表示城市,边表示路线,权值表示路线成本。图G可能存在多棵不同的生成树,其中一定存在一棵总成本最小的生成树,即该生成树上各边的权值之和最小,称为最小生成树。 常用的最小生成树构造法有两种:普里姆算法和克鲁斯卡尔算法。 假设对连通带权图G=(V,E)构造的最小生成树为子图T。普里姆算法的基本步骤如下: (2)找出集合U(已选入生成树的顶点集)和集合V-U(为选入生成树的顶点集)之间权值最小的边(uj,vk),其中uj∈U,vk∈V-U,简称最小边。 (3)重复步骤(2),直到U=V为止,T为所求的最小生成树。 普里姆算法的关键在于找出最小边,引入一维数组clsedge: 对于集合V-U中的每个顶点vi,closedge[i]存储该顶点与当前集合U之间的最小边信息。 在数组中按lowcost域找到最小值即为最小边的权值。顶点vi加入集合U时,将closedge[i].lowcost置为0.普里姆算法的步骤如下: (1)假设从顶点vi出发构造最小生成树,初始子图T只包含顶点vi: closedge[i].lowcost=0 vi∈U closedeg[j]={i,Wij} vj∈V-U (2)选择其余n-1个顶点,重复执行以下步骤。 ①在closedge数组中按lowcost域找到最小值closedge[k],k∈V-U,则最小边为(k,closedge[k].adjInd),将vk加入到集合U,即置closedge[k].lowcost=0,并将k顶点和边(k,closedge[k].adjInd)加入到子图T中。 更新closedge数组。由于集合U中新加入顶点vk,需判断集合V-U中所有顶点和顶点vk的边的权值是否更小,若是则更新closedge数组的值,即若Wkj 为了实现方便,调用函数InitGraph_M(T,G,kind,G.vexs,G.n)初始化一个包含n个顶点且无边的子图T,同时利用标志数组G.tags记录顶点是否已经被选入T,每当vi顶点入选时,置G.tags[i]为SELECTED。 算法:普里姆算法 当最小生成树T采用邻接数组存储结构时,初始化T的时间复杂度为O(n2),构造T是双重循环结构,外层循环n-1次,内层两个n-1次的并列循环,分别求当前最下边和更新closedge数组,整个算法的时间复杂度为O(n2),与带权图中的边数无关,因此适合于求有较多边或弧的图(稠密图)的最小生成树。 假设连通带权图G=(V,E),设构造的最小生成树为子图T。克鲁斯卡尔算法的基本思想为: 克鲁斯卡尔算法的实现有以下两个关键问题: 算法:克鲁斯卡尔算法 当图G和最小生成树T采用邻接表存储结构时,初始化T和并查集S的时间复杂度均为O(n);取G中边需遍历邻接表中所有顶点,时间复杂度为O(n+e);构造包含所有边的最小堆H的时间复杂度为O(e);构建T是双重循环结构,外层循环e次,内层循环是两个并列操作,分别取权值最小的边和并查集的合并,总时间复杂度为O(e+(loge+logn))。图中e的数量级一般不低于n,因此算法的时间复杂度为O(eloge),与带权图中的边数有关,适合于求有较少边或弧的图的最小生成树。 生活中常遇到路径选择问题,例如从城市A到城市B,有人选择最短时间的路径,有人选择最省钱的路径。如果用图的顶点表示城市,带权边表示城市之间的路径,权值表示是时间或价格,则上述路径选择均属于最短路径问题。在带权图中,路径长度为路径上各边的权值之和,最短路径是指路径长度最小的路径。 常见的最短路径问题有两种:单点源最短路径和顶点之间的最短路径。单点源最短路径问题求从源点到其他所有顶点的最短路径,迪杰斯特拉算法是解决这一问题的经典算法;而顶点之间的最短路径问题是求图中每一对顶点之间的最短路径,对每个顶点执行迪杰斯特拉算法即可,也可以直接利用弗洛伊德算法。 迪杰斯特拉算法的基本策略是按最短路径长度的升序求得源点v到其他所有顶点的最短路径,依次记为P1,P2,…,Pi,…,Pn-1,Pi的终点记为vi。 若源点v到其他所有顶点的最短路径集P={P1,P2,…,Pi,…,Pn-1 }是升序集,则P具有以下两种性质: 证明(反证法):假设下一条求得的最短路径Pi+1不经过以求得最短路径的顶点,而经过其他顶点vj(i+1 与求最小生成树的普里姆算法类似,迪杰斯特拉算法也将图G的顶点集V分成两个子集U和V-U,U是已经求得最短路径的顶点集。用一维数组Dist记录集合V-U中各顶点所求的当前最短路径信息。其定义如下: 借助Dist数组,迪杰斯特拉算法的步骤如下: (1)假设源点vi,初始: U={源点vi} V-U={除源点vi之外的其他顶点} Dist[i]={-1,0} vi∈U Dist[j]={i,Wij} vj∈V-U且 Dist[j].lowcost=INFINITY vj∈V-U且 为了实现方便,用标志数组G.tags记录顶点是否在集合U中,每当顶点vi加入集合U时,置G.tags[i]为SELECTED。 算法:迪杰斯特拉算法 算法:输出源点到顶点k的最短路径 和普利姆斯算法类似,迪杰斯特拉算法也是双重循环结构,外层循环n-1次,内层有两层并列循环,第一个求当前最短路径,循环n-1次,第二个更新Dist数组,循环次数与顶点的出度相关,整个算法的时间复杂度为O(n2)。 为一组任务制定进度计划,比如课程或建筑任务,任务之间通常存在一定的次序关系,必须在一些任务完成之后才能开始另一些任务。对于整个任务,人们通常关心这样的问题:如何以某种线性顺序组织这些任务,以便能在满足所有次序关系的基础上逐个完成各项任务。这一问题可以用有向无环图进行建模,有向无环图是指不存在回路的有向图(DAG),其中顶点代表任务,弧代表任务之间的次序关系。 在DAG中,将所有顶点在不违反前后次序关系的前提下排成的序列称为拓扑有序序列,简称拓扑序列。构造拓扑序列的过程称为拓扑排序。 对于任意一个有向图,其拓扑排序过程如下: 在实现时由于不能破坏图的结构,可将删除顶点及其所引出的弧改为将该顶点的所有邻接顶点的入度减1.为此,用一维数组indegree保存每个顶点的入度,并用队列Q保存当前所有为输出的入度为0的顶点。 算法:拓扑排序 图G采用邻接表存储结构,计算每个顶点的入度须扫描邻接表中所有顶点,时间复杂度为O(e+n);建立入度为0的顶点队列,需扫描数组indegree,时间复杂度为O(n);若G无回路,则每个顶点入队和出队一边,且出队时还要扫描该顶点的邻接顶点的邻接表,将其每个邻接顶点的入度减1,时间复杂度为O(n+e)。因此整个算法时间复杂度为O(n+e)。 在一个带权有向图中,如果顶点表示事件,弧表示活动,弧上的权值表示活动持续的时间,则称该图为边代表活动网(AOE网)。 在现实中,AOE网可以用来描述一个工程的实施过程。AOE网除了能描述工程中活动的次序关系之外,还能分析“完成整个工程所需的最短时间”,“哪些活动会影响整个工程工期”等关键问题,这些问题对工程的整体规划具有重要意义。 由于工程只有唯一一个开始点和结束点,故在正常情况下,称AOE网中唯一一个入度为0的点为源点,唯一一个出度为0的点为汇点。 要估算完成整个工程所需的最短时间,就是要找一条从源点到汇点的最长路径(即权值之和最大的路径),该路径称为关键路径,关键路径上的活动称为关键活动,这些活动是影响整个工程工期进度的关键。 假设AOE网包含n个事件v0,v1,…,vn-1,和m个活动a1,a2,…,am,v0是源点,vn-1是汇点。求关键路径的问题有以下4个相关概念。 (1)事件vi的最早发生时间ve(i)。根据AOE网的定义,只有进入事件vi的所有活动均完成,事件vi发生的最早时间是从源点v0到vi的最长路径长度。弧 ve(i)可定义为如此下的递推公式: ve(0)=0 ve(vi)=Maxmk=1{ve(vjk)+Wjk->i} 若 由递推公式可知,其计算过程是从源点出发,沿各个弧(活动)一步一步推导到汇点,其过程与拓扑排序过程一致。 (2)时间vi的最迟发生时间vl(i)。事件vi的最迟发生时间是指在不影响整个工程工期的情况下,时间vi可以最迟发生的事件。由此进一步可知,事件vi最迟发生时间不能影响其所有后继事件(若存在弧< vi,vj>,则称vj为vi的后继事件)的最迟发生时间。 vl(i)可定义为如下的递推公式: vl(n-1)=ve(n-1) vl(i)=Minmk=1{vl(vjk)-Wi->jk} 若 (3)活动ak的最迟开始时间al(k)。根据AOE网的定义,若存在表示活动ak的弧 ae(k)=ve(i) 1≤k≤m (4)活动ak的最迟发生时间al(k)。若存在表示活动ak的弧 al(k)=vl(j)-Wij 显然,若活动ak的最迟开始时间和最早开始时间相等,则表示活动ak必须如期完成,否则将影响整个工程进度,该活动是关键活动。 由上述定义可知,关键路径的计算过程是,首先,按拓扑排序过程,依次计算出所有事件的最早发生事件,对事件vi,更新其后继事件vj的最早发生时间,若ve(j) 其次,按逆拓扑序列,依次计算所有事件的最迟发生时间。对事件vi,更新其最迟发生时间,对于vi的所有后继事件vj,若vl(i)-Wij,vl(i)=vl(j)-Wij,否则不变。 然后,再计算活动的最早发生时间和最迟开始时间。存在弧 由计算过程的讨论可知,计算事件最早发生时间ve(i)须在拓扑排序基础上进行,因此,须对拓扑排序算法做如下修改: 算法:计算ve(i) 同理,计算事件最迟发生事件vl(i)需要进行如下操作: 在此基础上,根据定义计算每个活动(即弧)的最早开始时间ae和最晚发生时间al,若ae=al,则为关键活动。 算法:求解关键路径 整个计算过程要对邻接表中所有结点进行扫描,时间复杂度为O(n+e)。8.2.1 邻接数组
#define UNVISITED 0
#define VISITED 1
#define INFINITY MAXINT //计算机允许的整数最大值,即∞
typedef enum{DG,DN,UDG,UDN
}GraphKind;//图的4种类型,有向图、有向带权图、无向图、无向带权图
typedef struct{
VexType *vexs;//顶点数组,VexType是顶点类型,由用户定义
int **arcs; //关系数组,对无权图,用0或1表示相邻否
//对带权图,则为权值或INFINTY
int n,e;//顶点数和边(弧)数
GraphKind kind;//图的类型
int *tags;//标示数组,可用于在图的遍历中标记顶点访问与否
}MGraph;MGraph G2Status InitGraph_M(MGraph &G,GraphKind kind,VexType *vexs,int n);//初始化含有n个顶点且无边的kind类的图G
Status CreateGraph_M(MGraph &G,GraphKind kind,VexType *vexs,int n,ArcInfo *arcs,int e);//创建n个顶点和e条边的kind类图G,vexs为顶点信息,arcs为边信息
StatusDestoryGraph_M(MGraph &G);//销毁图G
int LocateVex_M(MGraph G,VexType v);//查找顶点v在图G中的位序
Status GetVex_M(MGraph G,int k,VexType &w);//取图G的k顶点的值到w
Status GetVex_M(MGraph &G,int k,VexType w);//将w的值赋给G的k顶点
int FirstAdjVex_M(MGraph G,int k);//求图G中k顶点的第一个邻接顶点的位序
int NextAdjVex_M(MGraph G,int k,int m);//m顶点为k顶点的邻接顶点,求图G中k顶点相对于m顶点的下一个邻接顶点的位序
Status AddArc_M(MGraph &G,int k,int m,int info);//在图G中增加k顶点到m顶点的边或弧,若为带权图,info为权值,否则为1
Status RemoveArc_M(MGraph &G,int k,int m);//在图G中删除k顶点到m顶点的边或者弧
Status DFSTraverse_M(MGraph G,Status(*visit)(int));//深度优先遍历图G
Status BFSTraverse_M(MGraph G,Status(*visit)(int));//广度优先遍历图G1.查找顶点
int LocateVex_M(MGraph G,VexType v)
{
//查找顶点v在图G中的位序
int i;
for(i=0;i2.创建无向图的邻接数组存储结构
typedef struct{
VexType v,w;//边(弧)的端点
int info;//对带权图,为权值
}ArcInfo;//边(弧)信息
Status CreateGraph_M(MGraph &G,GraphKind kind,VexType *vexs,int n,ArcInfo *arcs,int e)//创建n个顶点和e条边的kind类图G,vexs为顶点信息,arcs为边信息
{
if(n<0||e<0||(n>0&&NULL==vexs)||(e>0||NULL==arcs))\
{
return ERROR;
}
G.kind=kind;
switch(G.kind)
{
case UDG:
return CreateUDG_M(G,vexs,n,arcs,e);//创建无向图
case DG:
return CreateDG_M(G,vexs,n,arcs,e);//创建有向图
case UDN:
return CreateUND_M(G,vexs,n,arcs,e);//创建无向带权图
case DN:
return CreateDN_M(G,vexs,n,arcs,e);//创建有向带权图
default:
return ERROR;
}
}
Status InitGraph_M(MGraph &G,GraphKind kind,VexType *vexs,int n)//初始化含有n个顶点且无边的kind类的图G
{
int i,j,info;
if(n<0||(n>0&&NULL==vexs))
{
return ERROR;
}
if(kind==DG||kind==UDG)
{
info=0;//带权图
}
else if(kind==DN||kind==UDN)
{
info=INFINITY;//无权图
}
else
{
return ERROR;
}
G,n=n;G.e=e;//顶点数和边数
G.kind=kind;
if(n==0)
{
return OK;//空图
}
if(NULL==(G.vexs=(VexType *)malloc(VexType)))
{
return OVERFLOW;
}
for(i=0;iStatus CreateUDG_M(MGraph &G,VexType *vexs,int n,ArcInfo *arc,int e)
{
//创建含n个顶点和e条边的无向图G,vexs为顶点信息,arcs为边信息
int i,j,k;
VexType v,w;
if(InitGraph_M(G,G.kind,vexs,n)!=OK)
{
return ERROR;//初始化
}
G.e=e;//边数
for(k=0;k3.求第一个邻接顶点
int FirstAdjVex_M(MGraph G,int k)//求图G中k顶点的第一个邻接顶点的位序
{
int i;
if(k>0||k>G.n)
{
return -1;//k顶点不存在
}
for(i=0;i8.2.2邻接表
typedef struct AdjVexNode{
int adjvex;//邻接顶点在顶点数组中的位序
struct AdjVexNode *nextArc;//指向下一个邻接顶点(下一条边或弧)
int info;//存储边(弧)相关的=信息(如带权图的权值)
}AdjVexNode,*AdjVexNodeP;//邻接链表的结点类型
typedef struct VexNode{
VexType data;//顶点值,VexType是顶点类型,由用户定义
struct AdjVexNode *firstArc;//邻接链表的头指针
}VexNode;//顶点数组的元素类型
typedef struct{
VexNode *vexs;//顶点数组,用于存储顶点信息
int n,e;//顶点数和边(弧)数
GraphKind kind;//图的类型
int *tags;//标记数组,可用于在图的遍历中标记顶点访问与否
}ALGraph;//邻接表类型Status CreateGraph_AL(ALGraph &G,GraphKind kind,VexType *vexs,int n,ArcInfo *arcs,int e);//创建n个顶点和e条边的kind类图G,vexs为顶点信息,爱如潮水、为边(弧)信息
Status DestroyGraph_AL(ALGraph &G);//销毁图G
int LocateVex_AL(ALGraph G,VexType v);//查找顶点v在图G中的位序
Status GetVex_AL(ALGraph G,int k,VexType &w);//取图G的k顶点的值到w
Status PutVex_AL(ALGraph &G,int k,AdjVexNode w);//对图G的k顶点赋值w
int FirstAdjVex_AL(ALGraph G,int k,AdjVexNodeP &p);//若图G中k顶点的邻接链表非空,则令指针p指向第一个结点,并返回其存储的邻接顶点的位序,否则,令指针p为NULL,并返回-1
int NextAdjVex_AL(ALGraph G,int k,AdjVexNodeP &p);//在k顶点的邻接链表中,令p指向下一结点。若p非空,返回存储在p结点中的下一个邻接结点的位序,否则返回-1
Status AddArc_AL(ALGraph &G,int k,int m,int info);//在图G中增加k顶点到m顶点的边或弧,若为带权图,info为权值,否则为1
Status RemoveArc_AL(ALGraph &G,int k,int m);//在图G中删除k顶点到m顶点的边或弧
Status DFSTraverse_AL(ALGraph G,Status(*visit)(int));//深度优先遍历图G
Status BFSTraverse_AL(ALGraph G,Status(*visit)(int));//广度优先遍历图G1.创建有向图的邻接表存储结构
Status CreateDG_AL(ALGraph &G,VexType *vexs,int n,ArcInfo *arcs,int e)
{
//创建含有n个顶点和e条弧的有向图G,vexs为顶点信息,arcs为边信息。
int i,j,k;
VexType v,w;
AdjVexNodeP p;
G.n=n;G.e=e;//读入顶点数和弧数
G.vexs=(VexNode*)malloc(n*sizeof(VexNode));
G.tags=(int *)malloc(n*sizeof(int));
for(i=0;i2.插入边(弧)
Status AddArc_AL(ALGraph &G,int k,int m,int info){
//在图G中增加k顶点到m顶点的边或弧,若为带权图,info为权值,否则为1
AdjVexNodeP p;
if(k<0||k>=G.n||m<0||m>=G.n)
{
return ERROR;//k或m顶点不存在
}
if((UDG==G.kind||DG==G.kind)&&info!=1)
{
return ERROR;//info和图的类型不匹配
}
p=G.vexs[k].firstArc;
while(p!=NULL)//判断弧是否已存在
{
if(m==p->adjvex)//弧存在,返回
{
return ERROR;
}
p=p->nextArc;
}
p=(AdjVexNode*)malloc(sizeof(AdjVexNode));//为m顶点分配p结点
if(NULL==p)
{
return OVERFLOW;
}
p->adjvex=m;
p->info=info;
p->nextArc=G.vexs[k].firstArc;//在k顶点的邻接链表表头插入p结点
G.vexs[k].firstArc=p;
if(UDG==G.kind||UDN==G.kind)
{
p=(AdjVexNode*)malloc(sizeof(AdjVexNode));//为k顶点分配p结点
if(NULL==p)
{
return OVERFLOW;
}
p->adjvex=k;
p->info=info;
p->nextArc=G.vexs[m].firstArc;//在m顶点的邻接链表表头插入p结点
G.vexs[m].firstArc=p;
}
G.e++;
return OK;
}2.求第一个邻接顶点
int FirstAdjVex_AL(ALGraph G,int k,AdjVexNodeP &p)
{
if(k<0||k>=G.n)
{
return -1;//k顶点不存在
}
p=G.vexs[k].firstArc;
if(p!=NULL)
{
return p->adjvex;//返回第一个结点存储的顶点位序
}
else return -1;//k顶点无邻接顶点
}3.求下一个邻接顶点
int NextAdjVex_AL(ALGraph G,int k,AdjVexNodeP &p)
{
if(k<0||k>=G.n)
{
return -1;//k顶点不存在
}
if(NULL==p)
{
return -1;//指针p为空
}
p=p->nextArc;//令p指针指向下一个结点
if(p!=NULL)
{
return p->adjvex;//返回p结点存储的下一个邻接顶点的位序
}
else
{
return -1;//k顶点无下一个邻接顶点
}
}Status visitAllAdjVex(ALGraph G,int k,Status(*visit(int)))
{
int i;
AdjVexNodeP p=NULL;
if(k<0||k>G.n)
{
return ERROR;
}
for(i=FirstAdjVex_AL(G,k,p);i>=0;i=NextAdjVex(G,k,p))
{
if(ERROR==visit(i))
{
return ERROR;
}
}
return OK;
}8.3 图的遍历
8.3.1 深度优先遍历
Status DFS_M(MGraph G,int k,Status(*visit)(int))
{
//从连通图G的顶点出发进行深度优先遍历,图G采用邻接数组存储结构
int i;
if(ERROR==visit(k))
{
return ERROR;//访问顶点k失败
}
G.tags[k]=VISITED;
for(i=FirstAdjVex_M(G,k);i>=0;i=NextAdjVex_M(G,k,i))
{
if(UNVISITED==G.tags[i])//位序为i的邻接顶点违背访问过
{
if(ERROR==DFS_M(G,i,visit))
{
return ERROR;//对i顶点递归深度遍历
}
}
}
}Status DFSTraverse_M(MGraph G,Status(*visit)(int))
{
//深度优先遍历次啊用邻接数组存储结构的图G
int i;
for(i=0;i8.3.2 广度优先遍历
Status BFSTraverse_AL(ALGraph G,Status(*visit)(int)){
//广度优先遍历采用邻接表存储结构的图G
int i,j,k;
AdjVexNodeP p;
LQueue Q,InitQueue_LQ(Q);//初始化链队列Q
for(i=0;i8.3.3 遍历的应用
Status isReachable_DFS(MGraph G,int s,int t)
{
//判断有向图G中是否存在从顶点s到顶点t的路径,图G采用邻接数组存储结构
int i;
Status found=FALSE;//标识是否找到终点t
G.tags[s]=VISITED;
if(s==t)
{
return TRUE;//一旦遇到终点t,遍历终止
}
for(i=FirstAdjVex_M(G,s);i>=0&&FALSE==found;i=NextAdjVex_M(G,s,i))
{
if(UNVISITED==G.tags[i])
{
found=isReachable_DFS(G,i,t);//保存查找结果
}
}
return found;//继续返回查找结果
}void ShortestPathLength_BFS(ALGraph G,int s,int *D)
{
//求无向图G中s到各顶点的最短路径长度,图G采用邻接表存储结构
int i,j;
AdjVexNodeP p;
LQueue Q;InitQueue_LQ(Q);
for(i=0;i8.4 最小生成树
8.4.1普里姆算法
(1)若从G的顶点vi开始构造最小生成树,则T初始为只包含顶点vi且无边的图,即T=({vi},{})。typedef struct
{
int adjInd;//U中顶点的位序
int lowcost;//边的权值
}ClosedgeInfo;//U-V的顶点和当前U之间的最小边信息
ClosedgeInfo *closedeg;#define SELECTED 1
#define UNSELECTED 0
Status Prim(MGraph G,int i,MGraph &T){
//用普里姆算法从i顶点出发构造图G的最小生成树T,图G和T采用邻接数组存储结构
int j,min,k,m=0;
ClosedgeInfo*closedge;
closedge=(ClosedgeInfo*)malloc(G.n*sizeof(ClosedgeInfo));
InitGraph_G(T,G,kind,G.vexs,G.n);//初始化含n个顶点且无边的T
for(j=0;j8.4.2 克鲁斯卡算法
typedef struct{
int v,w;
KeyType key;//边的权值
}RcdType;//边的信息
Status Kruskal(ALGraph G,ALGraph &T){
//用克鲁斯卡尔算法构造图G的最小生成树T,图G和T采用邻接表存储结构
int i,j,v,w;
MFSet S;
Heap H;
RcdType temp,*arcs;
AdjVexNodeP p;
T.n=G.n;
T.e=0;
T.kind=G.kind;//初始化T
T.vexs=(VexNode*)malloc(G.n*sizeof(VexNode));
for(i=0;i8.5 最短路径
typedef struct{
int prev;//当前最短路径上该顶点的前驱顶点的位序
int lowcost;//当前最短路径的长度
}DisInfo;//V-U中顶点的当前最短路径信息
DisInfo *Dist;
Status Dijkstra(ALGraph G,int i,DistInfo &*Dist){
//求图G中从顶点i到其他顶点的最短路径,并由Dist返回
int j,m,k,min;
AdjVexNodeP p;
Dist=(DistInfo*)malloc(G.n*sizeof(DistInfo));
for(j=0;jvoid Outputpath(ALGraph G,DistInfo *Dist,int k)
{
//沿Dist数组prev域,可递归获得源点到k顶点的最短路径
if(-1==k)
{
return ;
}
Outputpath(G,Dist,Dist[k].prev);//逆向递归获取路径上的顶点
printf("%c",G.vexs[k].data);//正向输出当前路径上的顶点
}8.6 拓扑排序
Status ToplogicalSort(ALGraph G){
//对采用邻接表存储结构的图G进行拓扑排序
int i,cout=0,*indegree;
AdjVexNodeP p;
indegree=(int *)malloc(G.n*sizeof(int));
LQueue Q;
InitQueue_LQ(Q);//初始化链队列Q
for(i=0;i8.7 关键路径
Status VE_TologicalSort(ALgraph G,SqStack &S,int *ve){
int i,j,count=0,*indegree;
AdjVexNodeP p;
indegree=(int *)malloc(G.n*sizeof(int));
LQueue Q;InitQueue_LQ(Q);//初始化链队列Q
for(i=0;i
typedef struct{
VexType v,w;
int info;
int ae,al,le;//活动的最早开始时间、最晚开始时间以及两者之差
}Activity;//活动信息
Status CriticalPath(ALGraph G,Activity *A){
int i,j,*ve,*vl,ae,al,k=0;
AdjVexNodeP p;
SqStack S;InitStack_Sq(S,G.n,G.n);
ve=(int *)malloc(G.n*sizeof(int));
vl+(int *)malloc(G.n*sizeof(int));
if(ERROR==VE_ToplogicalSort(G,S,ve)){
return ERROR;
}
for(i=0;i