pytorch入门第一天

今天作为入门pytorch的第一天。打算记录每天学习pytorch的一些理解和笔记，以用来后面回顾。当然如果能帮到和我一样的初学者，那也是不胜荣幸。作为一名初学者，难免有些地方会现错误，欢迎各位大佬指出

预备知识

这里主要介绍pytorch的矩阵一些相关知识。矩阵总所周知是神经网络里重要内容，信号传递等都需要用到矩阵的一些知识。
这里的矩阵和numpy库中基本相似。使用基本运算符+-*/和另一个矩阵相乘都是对应元素进行运算。如果需要矩阵间的乘法(主要使用的运算)这需要使用方法a.mm(b)这里就是矩阵a和矩阵b使用矩阵乘法

torch和numpy里矩阵的一些区别

首先在numpy里矩阵一般都是直接作为数字计算，不会纠结变量类型，但是在torch中有矩阵元素类型。如果两个矩阵类型不相同进行运算操作（例如矩阵乘法）可能会导致报错。在初始化时可以直接定义类型

import torch
a=torch.tensor([1,2],dtype=float)#定义时声明类型为float

其次在torch中tensor在较高版本的torch中和自动微风变量合并了。如果需要声明此变量是自动微分变量（自动微分变量通俗理解就是可以自动求导，方便更新参数），需要在定义时声明requires_grad参数为True

a=torch.tensor([1,2],requires_grad=True,dtype=float)

自动微分变量可以用来更新神经网络权重等。例如以下代码

x = torch.linspace(0, 100,100).type(torch.FloatTensor)
rand =torch.randn(100)* 10
y = x + rand
x_train = x[: -10]
x_test = x[-10 :]
y_train = y[: -10]
y_test = y[-10 :]
learning_rate = 0.0001
for i in range(1000):# 计算在当前a、b条件下的模型预测值
    predictions = a.expand_as(x_train) * x_train +b.expand_as(x_train)
    loss = torch.mean((predictions - y_train) ** 2) #损失
    loss.backward() # 对损失函数进行梯度反传
    a.data.add_(- learning_rate * a.grad.data)   
    b.data.add_(- learning_rate * b.grad.data)  
    a.grad.data.zero_() # 清空a的梯度数值   
    b.grad.data.zero_() # 清空b的梯度数值

上述代码可以实现对一个一元函数更新。
这里另一个需要注意的点时一个变量被声明为自动微分变量后将损失传递后会有梯度信息，这个信息如果再次更新是通过相加更新的，也就是说如果用完梯度信息后如果不对梯度进行清空会导致梯度累加，影响模型的训练

激活函数

目前我所学的激活函数有三种，分别是：

• sigmoid()函数，也就是logist函数，图像是
  
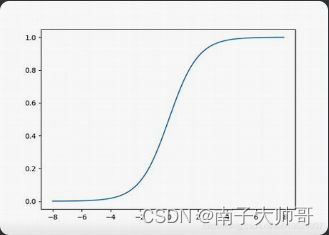
• softmax()函数，此函数就是使得结果相加等于1。目的是为了使结果为1。通常用于分类问题，使得所有输出节点值相加等于1.
• relu()函数，这也是通常用于分类问题。图像特点是
• 

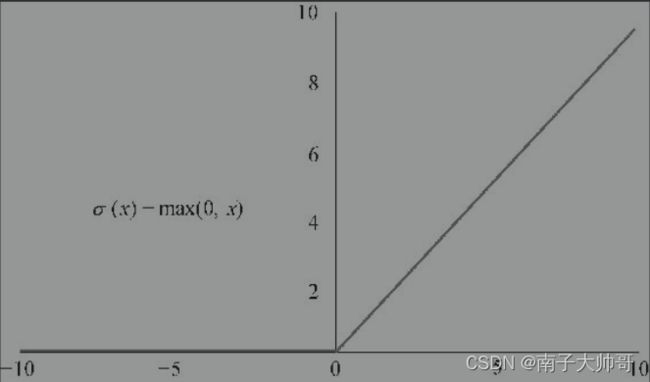
上述三个函数各有特点，目前学的就是在隐藏层用sigmoid激活函数，在输出层使用下面两个函数

编码处理

这里的编码处理是指神经网络输出结果的编码。对于问题通过有两种类型

• 对数字大小不敏感，数字只是作为一个结果或者现象的表示。例如天气，1代表天气，2代表下雨。此时大小无意义
• 对数字大小敏感，数字大小是结果的。例如重量

此时对这两种问题有两种不同措施：

• 对于第一种问题，通常采用一种名为独热编码的方式。就是将输出层设置多个节点，一个节点代表一个类型（例如表示天气，一个节点表示晴天一个表示雨天）结果有几个类型就有几个输出节点。输出节点中值最大的就是最终答案。

• 对于第二种问题，无需多少就是常规的方法，一个输出。但是这里通常需要使用归一化，这样可以加快训练速度。

torch自带的容器

torch自带神经网络容器（我也不知道是不是叫容器）。使用该容器可以快速构建一个神经网络。

import torch.nn as nn
model = nn.Sequential(   
	 	nn.Linear(len(diction), 10),
    	nn.ReLU(),    
   		nn.Linear(10, 2),  
     	nn.LogSoftmax(dim=1),)

Linear(a,b)函数是创建一个线性层，输入a个节点，输出节点数是b
这里有四个参数。分别是输入层到达隐藏层的权重、隐藏层的激活函数、隐藏层到达输出层的权重、输出层的激活函数。
使用该网络时直接将输入传入就会返回一个输出结果

output=model(input)

数据集的划分

一般的一个数据集通常划分为三个部分。分别是训练集、校验集、测试集。
其中训练集用来训练。
校验集用来验证是否出现过拟合等现象，这样可以及时调整超参数（学习率等）。如果出现过拟合现象通常是校验集的损失曲线上升等。
验证集用来验证最终训练结果的正确率。
通常上述三个集合比例是8：1：1。
很明显只要训练集的参数用来训练调整参数，校验集和验证集都不能用来训练调整参数，否则就失去了意义。