二值图像分析：轮廓形状逼近与拟合

1.二值图像轮廓逼近

1.1 轮廓逼近函数

在[二值图像分析：二值图像轮廓提取]，通过findContours()函数可以找到二值图像中的轮廓信息。对图像二值图像的每个轮廓，OpenCV提供了一个函数approxPolyDP()来对每个轮廓逼近它的的真实几何形状，从而通过轮廓逼近的输出结果判断一个对象是什么形状，或者得到一些其他信息。

OpenCV轮廓逼近的函数原型如下：

void cv::approxPolyDP(InputArray curve,OutputArray approxCurve,
					double epsilon,bool closed)

参数介绍：

• Curve：表示轮廓曲线，通常可以是findContours()中参数Contours里的元素，即一个由点集组成的轮廓。
• approxCurve： 可以设为vector保存轮廓逼近输出的折点。
• epsilon： 轮廓逼近的顶点距离真实轮廓曲线的最大距离，该值越小表示越逼近真实轮廓。
• close： 表示是否为闭合区域。

1.2 轮廓逼近算法原理分析

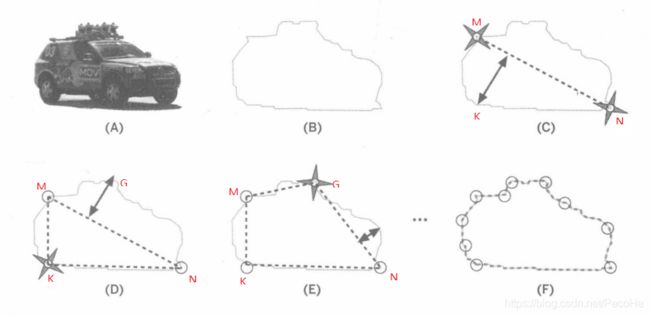
这里借用一下《学习OpenCV3》一书中的图像：

如上图，(A)为原始图像，（B）为经过一定处理后提取出来的轮廓。则轮廓逼近算法会对于该轮廓：

• 首先找到轮廓中距离最远的两个点，如图（C）中的M、N，将这2点连接，至此将轮廓逼近成了一条线段。
• 然后在原来的轮廓上找一点使得其离MN线段的距离最大，如K点，将MK，NK连接，至此将轮廓逼近成了一个三角形。
• 再在原来的轮廓上找一点使得其三角形MNK的距离最大，如G点，去除MN，将MG，NG连接，至此将轮廓逼近成了一个四边形。
• 如此反复迭代，将新的点加入到逼近的几何多边形状中去，直到轮廓上任意一点到多边形的距离小于设定的精度参数epsilon。

2.代码实践

#include 
#include 
#include 

using namespace std;
using namespace  cv;

int main(int argc,char**argv)
{

    Mat srcImage = imread("/mnt/hgfs/winshare/images/dp.png");

    if(srcImage.empty())
    {
        cout<<"load image failed."<<endl;
        return -1;
    }

    Mat grayImage,binaryImage;
    cvtColor(srcImage,grayImage,COLOR_BGR2GRAY);
	
	//处理成前景白色，背景黑色
    bitwise_not(grayImage,binaryImage);

	//轮廓提取
    vector<vector<Point>> contours;
    vector<Vec4i> hierarchy;
    findContours(binaryImage,contours,hierarchy,RETR_TREE,CHAIN_APPROX_SIMPLE,Point());

	//保存每一个轮廓的折点集
    vector<vector<Point>> contours_poly(contours.size());

    for(int i=0;i<contours.size();++i)
    {
        approxPolyDP(contours[i],contours_poly[i],10,true);
        for(int j=0;j<contours_poly[i].size();++j)
        {
        	//绘制出每一个折点
            circle(srcImage,contours_poly[i][j],2,Scalar(0,0,255),2,8,0);
        }

    }

    imshow("res",srcImage);
    waitKey(0);

    return 0;
}

运行结果：

3.最小外接圆拟合

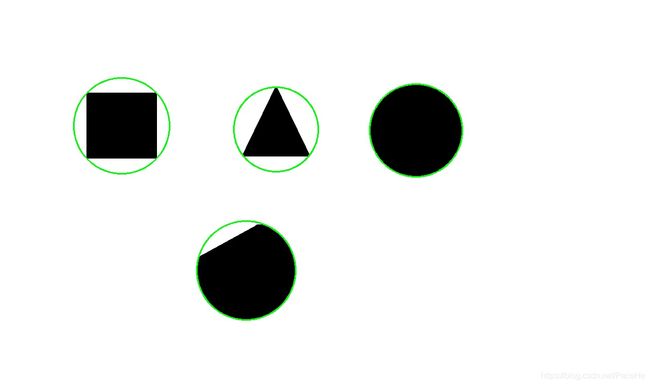
在上面的图中，下面一个圆明显缺了一角，实际应用中经常会有这样的情况，这个时候一般的圆检测算法，如霍夫圆检测就会失效。这种情况下可以使用最小包围圆逼近算法，前提是要把前景目标的轮廓弄平滑了，否则噪点会影响拟合结果。

OpenCV提供了一个函数来完成对一个轮廓的最小包围圈逼近：

void minEnclosingCircle( InputArray points,Point2f& center, 
				 float& radius );

参数解释：

• points：由点集组成的轮廓。
• center：输出圆心坐标。
• radius：输出圆的半径。

值得注意的是，C++语法不支持函数有多个返回值，所以没法将圆心坐标和半径一起返回，因此需要提前定义好坐标（Point2f类）和半径（float类型）来传递引用，作为输出型参数接收结果传递给函数。

代码实践：

#include 
#include 
#include 

using namespace std;
using namespace  cv;

int main(int argc,char**argv)
{
    Mat srcImage = imread("/mnt/hgfs/winshare/images/dp.png");

    if(srcImage.empty())
    {
        cout<<"load image failed."<<endl;
        return -1;
    }

    Mat grayImage,binaryImage;
    cvtColor(srcImage,grayImage,COLOR_BGR2GRAY);

    bitwise_not(grayImage,binaryImage);
    //imshow("binaryImage",binaryImage);

    vector<vector<Point>> contours;
    vector<Vec4i> hierarchy;
    findContours(binaryImage,contours,hierarchy,RETR_TREE,CHAIN_APPROX_SIMPLE,Point());

    vector<vector<Point>> contours_poly(contours.size());

    for(int i=0;i<contours.size();++i)
    {
    	//定义center和r用来接收结果
        Point2f center;
        float r;
        minEnclosingCircle(contours[i],center,r);

        circle(srcImage,center,r,Scalar(0,255,0),2,8,0);
    }

    imwrite("/home/peco/Desktop/resDP.jpg",srcImage);

    waitKey(0);

    return 0;
}

运行结果如下，可以看到对于不完整的圆也有很准确的检测效果：

4.最大内接圆拟合

4.1 点轮廓位置测试函数

OpenCV提供了一个函数来帮助判断一个点和轮廓的位置关系：

double pointPolygonTest( InputArray contour, Point2f pt, 
						bool measureDist );

该函数可以准确计算出一个点距离某个轮廓的距离，如果该点在轮廓上，返回的距离就是0；如果是在外部或者内部，则分别返回负数和正数表示距离。它的参数解释如下：

• contour：点集组成的轮廓。
• pt：要判断的点。
• measureDist：设为True时返回实际点到轮廓的距离，设为False返回0（表示点在轮廓上）或者1（表示点在轮廓外）或者-1（表示点在轮廓内）三者中的一个。

4.2 获取轮廓最大内接圆

有了上面的函数之后，获取轮廓最大内接圆就很容易了。由于点轮廓测试函数返回的是点到轮廓的最短像素距离，那么我们只要扫描轮廓内部的点，找到内部点中到轮廓距离最大的点，这个距离就是最大内接圆的半径，该点就是圆心。

对于下面的输入图像：

代码实践：

#include 
#include 
#include 

using namespace std;
using namespace  cv;


int main(int argc,char**argv)
{
    Mat srcImage = imread("/mnt/hgfs/winshare/images/dp_1.png");

    if(srcImage.empty())
    {
        cout<<"load image failed."<<endl;
        return -1;
    }

    Mat grayImage,binaryImage;
    cvtColor(srcImage,binaryImage,COLOR_BGR2GRAY);

    vector<vector<Point>> contours;
    vector<Vec4i> hierarchy;
    findContours(binaryImage,contours,hierarchy,RETR_EXTERNAL,CHAIN_APPROX_SIMPLE,Point());

    Mat dstIMage(srcImage.size(),CV_32F);
    for(int i=0;i<srcImage.rows;++i)
    {
        for(int j=0;j<srcImage.cols;++j)
        {
            dstIMage.at<float>(i,j) = (float)pointPolygonTest(contours[0],
                    Point2f((float)j,(float)i),true);
        }
    }

    double min,max;
    Point minLoc,maxLoc;
    minMaxLoc(dstIMage,&min,&max,&minLoc,&maxLoc);

    cout<<"Min :"<<min<<",Loc:("<<minLoc.x<<","<<minLoc.y<<")."<<endl;
    cout<<"Max :"<<max<<",Loc:("<<maxLoc.x<<","<<maxLoc.y<<")."<<endl;

    circle(srcImage,minLoc,2,Scalar(0,0,255),2,8,0);
    circle(srcImage,maxLoc,2,Scalar(0,0,255),2,8,0);
    circle(srcImage, maxLoc, (int)max, Scalar(0, 255, 0),2,8,0);


    imwrite("/home/peco/Desktop/resDP.jpg",srcImage);

    waitKey(0);

    return 0;
}

输出：

Min :-610.021,Loc:(1262,747).	#输出结果右下角红点
Max :107.336,Loc:(574,345).		#中心处红点

运行结果：