华为第二批难题五：AI技术提升六面体网格生成自动化问题

有CAE开发商问及OCCT几何内核的网格方面的技术问题。其实，OCCT几何内核的现有网格生成能力比较弱。

HybridOctree_Hex的源代码，还没有仔细去学习。

“HybridOctree_Hex”的开发者说：六面体网格主要是用在数值模拟领域的，比如汽车飞机或者是医疗影像行业给病人核磁共振扫描后做数字孪生的。图形学领域由于主要是服务游戏和影视行业，一般只关注物体的表面，用三角形网格，因此不是这个软件的受众。

Marching Cubes算法和六面体网格划分在空间处理和结果表示上有所不同，前者是一种等值面的提取和可视化表示的算法，而后者是后续的空间的数值计算和分析。在比较复杂的网格上直接用Marching Cube生成的体积网格不仅有可能不是全六面体的（全六面体一般在数值模拟里精度最高最受青睐），而且在表面附近大概率是有自交叉或者是负雅可比的。我们这个算法主要是聚焦对表面区域网格质量的优化，同时确保所有点都贴合在原始表面上。你如果对六面体网格生成有兴趣的话，可以看看这篇综述：dl.acm.org/doi/pdf/10.1。

总的来说，四面体网格的自动生成已经被内嵌到一些商业软件里了（HyperMesh, ANSYS, ICEM, Cubit），一些自研的小软件也很好用（TetGen, TetWild）。六面体-四面体混合网格在之前提到的软件里也有比较成熟的解决方案。但是纯六面体网格目前还是一个开放问题，在速度-鲁棒-质量三角中没有任何一个算法能够通吃。目前比较有竞争力的算法有我们这种基于背景网格点的八叉树法（速度快，非常鲁棒），还有frame field算法（slides.games-cn.org/pdf）和基于polycube的算法（dl.acm.org/doi/pdf/10.1，质量高）。这三种算法在那个综述里都有介绍，后两种算法在可预见的几年里应该仍然会停留在实验室阶段，因为虽然其质量高，但剩下两个板子太短了，速度非常慢，鲁棒性上frame field无法保证切出来的每个多面体都是六面体，所以网格可能是六面体-四面体混合的。polycube算法在将规则的几何体变形贴合到输入形状时有大量的超参数要调教，在复杂的几何体上没有人为干预很有可能会失败。八叉树法最大的短板是网格内奇异点多，以及部分因为这个原因导致的网格质量差。我们这次的工作主要是解决了网格质量差的问题，利用能量最小化算法，证实了八叉树法生成的网格质量也可以提高到非常高，以至于和其他算法的网格质量在缩放雅可比这一最广泛使用的网格指标上分庭抗礼甚至超越。在我们这个算法之前，八叉树法赛道下的最好算法是onlinelibrary.wiley.com和dl.acm.org/doi/pdf/10.1这两篇。他们是用了表面映射技术，去搜索一个原始表面到core mesh表面（有棱有角的内部网格）的映射。结果表明我们新算法在速度和质量上都会比这种映射算法高/快很多

基于混合八叉树和能量最小化方法的六面体网格划分程序——“HybridOctree_Hex”。不仅功能强大，而且操作简单。

HybridOctree_Hex全六面体网格生成的五个步骤。

(a)从表面三角形（红色）初始化八叉树网格，自动识别大曲率和狭窄区域；

（b）将初始化的八叉树转换为强平衡八叉树，满足平衡规则和配对规则；

（c）使用预定义模板构建全六面体对偶网格；

（d）清除边界外和周围的元素；

（e）全局坐标优化

首先在(a)中，HybridOctree_Hex能够自动检测输入模型的曲率和狭窄区域，从而识别出关键表面特征，并据此初始化一个八叉树结构。这步操作相当关键，因为它能帮助我们快速找到模型中的重要信息。

接下来在(b)中，这款软件会构建一个强平衡八叉树。这一步是借鉴了我们之前的工作，通过一些特殊的规则来确保树结构满足平衡规则和配对规则。有了这个强平衡八叉树，我们就可以直接生成全六面体的对偶网格(c)。这里有个小技巧，我们预先定义了一些模板，这样就可以跳过复杂的切割和对偶构建步骤，提高了效率。

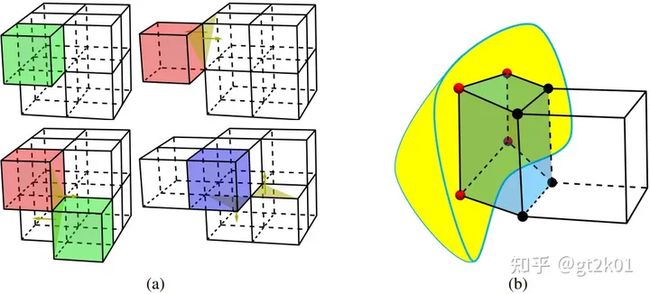
八叉树转换预定义模板。(a-e) 展示了强平衡的八叉树（第一行），混合对偶网格（第二行），以及转换模板（第三和第四行）

然后在(d)中，HybridOctree_Hex会移除网格外部和边界周围的部分，只保留内部网格。这个核心网格的边界点会与表面上的对应点相连，从而填充缓冲区并构建最终的网格。这里有一个小细节，我们从雅可比行列式的矢量三重积形式出发，对表面上会导致在填充缓冲区时形成低雅可比，甚至非流形网格的单元进行删除。这一步骤也是最终能够将最小缩放雅可比提高到0.5以上的关键。

（a）与组里之前的表面移除方法的对比。两种方法均去除的六边形为红色，之前的工作去除的六边形为绿色，通过我们的方法去除的六边形是蓝色。阴影的黄色三角形表示它们的法线满足我们的移除规则；（b）缓冲层的形成

最后在(e)中，为了将缓冲区的点全部投影到三角形网格边界上，并同时控制网格质量，HybridOctree_Hex还结合了Laplacian平滑算法和能量最小化算法。能量项由表面拟合度（此项最终需要严格降到0以确保对原始表面的还原）、Jacobian和缩放Jacobian三项组成，使用梯度下降算法进行优化。这里是我们文章的主要创新点，我们对雅可比行列式的性质进行了深入研究，详细内容可看文章。

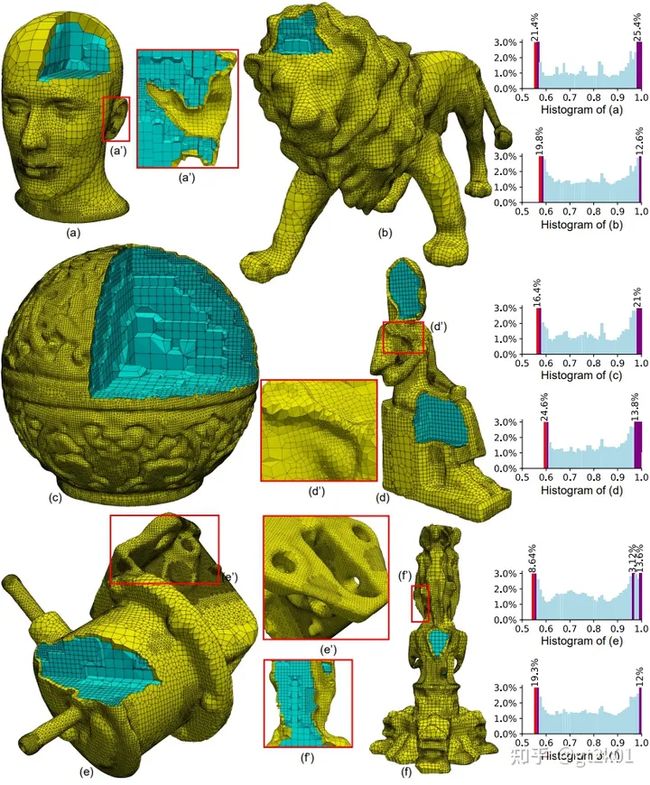
我们用HybridOctree_Hex对几十个复杂的3D模型进行了处理，结果都非常满意。无论是模型的细节还原还是网格质量，都处理得相当到位。我们的质量优化算法能够将最小缩放雅可比提升到0.5以上，远远超过以往算法。我们在文中挑出了最难的12个模型进行展示。

（a）瓶子1；（b）兔子；（c）大卫；（d）变形的犰狳；（e）龙台；（f）石像鬼。最后一列显示了缩放后的雅可比直方图。红色条代表最小缩放雅可比，紫色条由于频率较高（≥ 3%）而被截断

（a）头部；（b）狮子重建；（c）红色圆形盒子；（d）拉姆西斯；（e）油泵；（f）泰国雕像

这一方法还存在一些缺陷。最大的缺陷是计算时间。虽然相比之前的方法，我们在时间上已经取得了提升，但当前的计算速度还无法满足工程实际需求。不过这里也有代码实现的问题。我们的代码在很多细节没有对时间和空间复杂度进行优化，更多是进行了可行性的研究，感兴趣的朋友可以深入研究代码细节！另一缺陷则是在于算法本身——雅可比行列式只是网格合格的必要不充分条件，因此在未来的改进中，需要在能量项中引入更加全面的指标来确保网格的可使用性。

[Submitted on 11 Jan 2024 (v1), last revised 14 Jan 2024 (this version, v2)]

HybridOctree_Hex: Hybrid Octree-Based Adaptive All-Hexahedral Mesh Generation with Jacobian Control

Hua Tong, Eni Halilaj, Yongjie Jessica Zhang

We present a new software package, "HybridOctree_Hex," for adaptive all-hexahedral mesh generation based on hybrid octree and quality improvement with Jacobian control. The proposed HybridOctree_Hex begins by detecting curvatures and narrow regions of the input boundary to identify key surface features and initialize an octree structure. Subsequently, a strongly balanced octree is constructed using the balancing and pairing rules. Inspired by our earlier preliminary hybrid octree-based work, templates are designed to guarantee an all-hexahedral dual mesh generation directly from the strongly balanced octree. With these pre-defined templates, the sophisticated hybrid octree construction step is skipped to achieve an efficient implementation. After that, elements outside and around the boundary are removed to create a core mesh. The boundary points of the core mesh are connected to their corresponding closest points on the surface to fill the buffer zone and build the final mesh. Coupled with smart Laplacian smoothing, HybridOctree_Hex takes advantage of a delicate optimization-based quality improvement method considering geometric fitting, Jacobian and scaled Jacobian, to achieve a minimum scaled Jacobian that is higher than 0.5. We empirically verify the robustness and efficiency of our method by running the HybridOctree_Hex software on dozens of complex 3D models without any manual intervention or parameter adjustment. We provide the HybridOctree_Hex source code, along with comprehensive results encompassing the input and output files and statistical data in the following repository

源码：stoneold/HybridOctree_Hex

难题五：AI技术提升六面体网格生成自动化问题

技术背景

1. 业务场景：在使用工业软件对各物理场问题分析过程中，相对于其他网格，六面体网格具有更好的计算精度、更高的计算效率、更强的抗畸变能力并能更自然地顺应边界和物理场的走向。目前，六面体网格主要依赖半自动半手工模式--扫掠法来得到。

2. 技术选题的关键性：六面体剖分以扫掠法为主，对一些复杂的工程问题，所需工作量要以人月甚至人年记。如能提升六面体网格生成自动化程度，将大幅减轻工程师的劳动强度，显著提升工作效率，缩短仿真时间和产品开发周期。

3. 技术选题的泛用性：六面体网格生成技术是工业软件和一些相关领域的通用技术，并不局限于某个特定的应用场景。

 

技术挑战

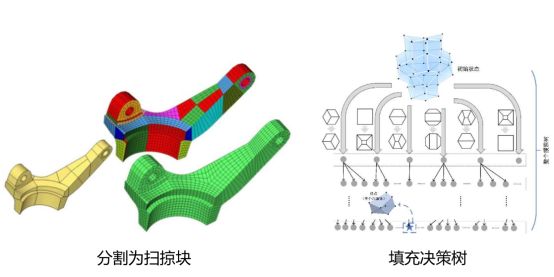
1. 设计基于AI的三维几何体分块算法，将物体分割为一些适合于扫掠的块。

2. 对于分割后剩余的不可扫掠块，设计AI指导下的空腔填充算法，以填充剩余块内部。

3. 空腔填充算法也应适用于四面体网格。

 

技术诉求

1. 可自动剖分模型的复杂程度：用基本体素进行10次以内布尔运算得出的几何模型(占比30%)。

2. 对更复杂模型可减少交互工作量30%以上。

3. 单元质量要求：雅可比值不低于0.1。

 

参考文献

[1] Pietroni N, Campen M, Sheffer A, et al. Hex-mesh generation and processing: a survey[J]. ACM TOG , 2022,42(2): 1-44.

[2] Fang X, Xu W, Bao H, and Huang J. All-Hex Meshing using Closed-Form Induced Polycube. ACM TOG , 2016; 35(4).

[3] Tautges TJ, Blacker T, Mitchell SA. The whisker weaving algorithm: A connectivity-based method for constructing all-hexahedral finite element meshes. IJNME, 1996; 39(19): 3327–3349.

[4] Price MA, Armstrong CG. Hexahedral mesh generation by medial surface subdivision: part II. Solids with flat and concave edges. IJNME, 1997; 40: 111-136.

[5] Livesu M, Pietroni N, Puppo E, Sheffer A, and Cignoni P. LoopyCuts: practical feature-preserving block decomposition for strongly hexdominant meshing. ACM TOG(SIGGRAPH) ; 2020: 39(4).

[6] Lu Y, Gadh R, Tautges TJ. Feature based hex meshing methodology: feature recognition and volume decomposition. Computer Aided Design, 2001; 33(3): 221–32.

[7] Lei, Na , et al. "Quadrilateral mesh generation II: Meromorphic quartic differentials and Abel-Jacobi condition." Computer Methods in Applied Mechanics and Engineering , 2020.

[8] Liu JF, Sun SL, Chen YQ. A new method of quality improvement for quadrilateral mesh based on small polygon reconnection, Acta Mechanica Sinica , 2012, 28(1):140-145.

[9] Biesbroeck A V , Shang F , Bassir D . CAD Model Segmentation Via Deep Learning[J]. International Journal of Computational Methods, 2020.

 

联系人：吴瑾    [email protected]