优化|复杂度分析——用于凸约束非凸优化问题的光滑化近似点增广拉格朗日算法
1. 简介
对于无约束的非凸优化问题,算法复杂度的下界为 Ω ( 1 / ϵ 2 ) \Omega(1/\epsilon^2) Ω(1/ϵ2);在目标函数光滑时,这个下界可以通过标准梯度下降算法来取到. 对于带约束的非凸优化问题,这个下界依旧适用;到这里,我们自然会提出疑问:它是否也能通过某个一阶算法来取到?
对此,本文 [ 1 ] ^{[1]} [1]作出了回答. 文中介绍了一种简单的一阶算法——光滑化近似点增广拉格朗日方法(Smoothed Proximal Augmented Lagrangian Method),并证明它可以取到这样的复杂度下界.
2. 问题与算法
2.1 问题背景
考虑
min f ( x ) s.t. A x = b , x ∈ X , ( 1 ) \begin{aligned} & \min ~ f(x) \\ \text{s.t.~} & Ax = b, ~x \in \mathcal{X}, \end{aligned} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (1) s.t. min f(x)Ax=b, x∈X,(1)
其中 A ∈ R m × n , b ∈ R m A \in\mathbb{R}^{m\times n},~ b \in \mathbb{R}^m A∈Rm×n, b∈Rm, X = { x ∣ h i ( x ) ≤ 0 , i = m + 1 , ⋯ m + l } \mathcal{X} = \{x ~| ~h_i(x)\leq 0, ~i = m+1,\cdots m+l\} X={x ∣ hi(x)≤0, i=m+1,⋯m+l} 是凸集, h i ( ⋅ ) : R n → R h_i(\cdot): \mathbb{R}^n \to \mathbb{R} hi(⋅):Rn→R 是光滑的凸函数. 目标函数 f ( ⋅ ) : R n → R f(\cdot): \mathbb{R}^n \to \mathbb{R} f(⋅):Rn→R 未必是凸的,其梯度满足 Lipschitz 连续条件. 不妨将 X \mathcal{X} X 的指示函数记作 ι ( ⋅ ) \iota(\cdot) ι(⋅),即
ι ( x ) = { 0 , 当 x ∈ X , ∞ , 其他 . \iota(x) = \begin{cases}0, & \text {当}~ x\in \mathcal{X}, \\ \infty, & \text {其他}. \end{cases} ι(x)={0,∞,当 x∈X,其他.
在实际应用中,我们的目标通常是找到问题 (1) 的一个 ϵ \epsilon ϵ-稳定点,它的定义为:
定义一 ( ϵ \epsilon ϵ-稳定点) 我们称 x ∈ X x\in\mathcal{X} x∈X 是问题 (1) 的一个 ϵ \epsilon ϵ-稳定点( ϵ ≥ 0 \epsilon\geq0 ϵ≥0),当且仅当存在 y ∈ R n y\in\mathbb{R}^n y∈Rn 和 v ∈ ∇ f ( x ) + A T y + ∂ ι ( x ) v \in\nabla f(x) + A^T y + \partial\iota(x) v∈∇f(x)+ATy+∂ι(x),满足 ∥ v ∥ ≤ ϵ \|v\|\leq\epsilon ∥v∥≤ϵ 和 ∥ A x − b ∥ ≤ ϵ \|Ax-b\|\leq \epsilon ∥Ax−b∥≤ϵ.
不难看出,取 ϵ = 0 \epsilon=0 ϵ=0 即对应问题 (1) 的稳定点.
2.2 算法框架
对于上述问题,常用的算法有增广拉格朗日算法(ALM)、交替乘子法(ADMM)以及罚函数方法等. 本文所考虑的是一种光滑化的近似点增广拉格朗日算法. 定义投影算子 P X ( x ˉ ) = arg min x ∈ X ∥ x − x ˉ ∥ 2 \mathcal{P}_{\mathcal{X}}(\bar{x}) = \arg \min _{x \in \mathcal{X}}\|x-\bar{x}\|^2 PX(xˉ)=argminx∈X∥x−xˉ∥2, 以及函数
K ( x , z ; y ) = f ( x ) + y T ( A x − b ) + γ 2 ∥ A x − b ∥ 2 + p 2 ∥ x − z ∥ 2 , K(x, z ; y)=f(x)+y^T(A x-b)+\frac{\gamma}{2}\|A x-b\|^2+\frac{p}{2}\|x-z\|^2, K(x,z;y)=f(x)+yT(Ax−b)+2γ∥Ax−b∥2+2p∥x−z∥2,
其中常数 γ ≥ 0 , p > 0 \gamma \geq 0,~ p>0 γ≥0, p>0.(当 p = 0 p=0 p=0 时, K ( ⋅ ) K(\cdot) K(⋅) 即对应问题 (1) 的增广拉格朗日函数.) 算法框架可以写成如下形式:
定义
d ( y , z ) = min x ∈ X K ( x , z ; y ) , x ( y , z ) = arg min x ∈ X K ( x , z ; y ) , d(y,z) = \min_{x\in\mathcal{X}}K(x,z;y), \quad x(y,z) = \arg\min_{x\in\mathcal{X}}K(x,z;y), d(y,z)=x∈XminK(x,z;y),x(y,z)=argx∈XminK(x,z;y),
P ( z ) = min x ∈ X , A x = b f ( x ) + p 2 ∥ x − z ∥ 2 , x ( z ) = arg min x ∈ X , A x = b f ( x ) + p 2 ∥ x − z ∥ 2 . P(z) = \min_{x\in\mathcal{X}, Ax=b} f(x)+\frac{p}{2}\|x-z\|^2, \quad x(z) =\underset{x\in\mathcal{X}, Ax=b}{\arg \min} f(x)+\frac{p}{2}\|x-z\|^2. P(z)=x∈X,Ax=bminf(x)+2p∥x−z∥2,x(z)=x∈X,Ax=bargminf(x)+2p∥x−z∥2.
可以证明,问题 (1) 等价于
min z P ( z ) , s.t. z ∈ R n . ( 2 ) \min_z P(z), \quad \text{s.t.}~ z \in \mathbb{R}^n. \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (2) zminP(z),s.t. z∈Rn.(2)
对于问题 (2) 的最优解 z ∗ z^{*} z∗ 而言, x ( z ∗ ) x(z^*) x(z∗) 是问题 (1) 的稳定点. 考虑求解问题 (2). 一方面,根据 Danskin 定理可知
∇ P ( z ) = p ( z − x ( z ) ) . \nabla P(z) = p(z-x(z)). ∇P(z)=p(z−x(z)).
由于涉及 x ( z ) x(z) x(z) 的求解, ∇ P ( z ) \nabla P(z) ∇P(z) 的精确值往往需要较大的计算量. 另一方面,我们可将算法中对 y t + 1 y^{t+1} yt+1 和 x t + 1 x^{t+1} xt+1 的更新看作是为求解 x ( z t ) x(z^t) x(zt) 而对原始、对偶变量进行的一步更新,因此 x t + 1 x^{t+1} xt+1 相当于 x ( z t ) x(z^t) x(zt) 的一个近似. 这样一来,算法中对于 z t + 1 z^{t+1} zt+1 的更新可看作是为求解问题 (2) 而做的一步近似梯度下降.
3. 收敛性结论
3.1 假设条件
结合 2.1 节的描述,文章做出如下假设:
假设1
(1) X \mathcal{X} X 是一个紧凸集;
(2) f f f 在 X \mathcal{X} X 上是下有界的函数(存在 f ‾ \underline{f} f,对任意 x ∈ X x \in \mathcal{X} x∈X 满足 f ( x ) > f ‾ > − ∞ f(x)>\underline{f}>-\infty f(x)>f>−∞);
(3) f f f 的梯度在 X \mathcal{X} X 上 L L L-连续,对应 Lipschitz 常数为 L f L_f Lf;
(4) h i ( i = m + 1 , ⋯ , m + l ) h_i ~(i = m+1, \cdots, m+l) hi (i=m+1,⋯,m+l) 是光滑凸函数,其梯度 L L L-连续,对应 Lipschitz 常数为 L h L_h Lh;
(5) Slater 条件成立.
其中,我们通过 Slater 条件可知 x ∗ ∈ R n x^* \in \mathbb{R}^n x∗∈Rn 是问题 (1) 的稳定点当且仅当它满足对应的 KKT 条件.
为了对算法在凸集 X \mathcal{X} X 上的收敛性进行分析,本文又提出了一个正则性假设. 我们用 J ( x ) ∈ R n × l J(x) \in \mathbb{R}^{n\times l} J(x)∈Rn×l 表示 ( h 1 ( x ) , ⋯ , h l ( x ) ) \left(h_1(x),\cdots,h_l(x)\right) (h1(x),⋯,hl(x)) 对应的 Jaccobian 矩阵,记 [ m ] = { 1 , ⋯ , m } [m]=\{1,\cdots,m\} [m]={1,⋯,m} 以及 [ m : n ] = { m , m + 1 , ⋯ , n } [m:n] = \{m,m+1,\cdots,n\} [m:n]={m,m+1,⋯,n}. 在此基础上,定义 Q ( x ) = [ A T J T ( x ) ] T Q(x) = [A^T~ J^T(x)]^{T} Q(x)=[AT JT(x)]T,积极不等式约束对应的指标集 I x = { i ∈ [ m + 1 : m + l ] ∣ h i ( x ) = 0 } \mathcal{I}_x = \{i \in [m+1:m+l] ~| ~h_i(x)=0\} Ix={i∈[m+1:m+l] ∣ hi(x)=0} 以及所有积极约束对应的指标集 S x = [ m ] ∪ I x \mathcal{S}_x =[m]\cup\mathcal{I}_x Sx=[m]∪Ix. 另外,对于 S ⊆ [ m + l ] \mathcal{S} \subseteq [m+l] S⊆[m+l],我们用 Q S ( x ) Q_{\mathcal{S}}(x) QS(x) 表示 Q ( x ) Q(x) Q(x) 取出 S \mathcal{S} S 对应列所得到的矩阵. 利用这些符号,正则性假设可以写成:
假设2 对任意的最优解 x ∈ X ∗ x \in \mathcal{X}^{*} x∈X∗, 都存在一个邻域,使得邻域内任意点 x x x 对应的矩阵 Q S x ( x ) Q_{\mathcal{S}_x}(x) QSx(x) 有相同的秩.
在这些条件下,可证明算法对于问题 (1) 有着 O ( 1 / ϵ 2 ) O(1/\epsilon^2) O(1/ϵ2) 的收敛速率. 实际上,如果 h i ( i = m + 1 , ⋯ , m + l ) h_i ~(i=m+1, \cdots, m+l) hi (i=m+1,⋯,m+l) 都是线性的,那么 X \mathcal{X} X 的紧性、Slater 条件和正则性假设都可以省去,我们只需要假设 2.1 中的条件 (2) 和 (3) 就可以证明上述收敛性结论 [ 2 ] ^{[2]} [2].
3.2 收敛率证明
结合 3.1 节的内容,本文将势能函数定义为:
ϕ t = K ( x t , z t ; y t ) − 2 d ( y t , z t ) + 2 P ( z t ) . \phi^{t} = K(x^t,z^t;y^t) - 2d(y^t,z^t) + 2P(z^t). ϕt=K(xt,zt;yt)−2d(yt,zt)+2P(zt).
关于势能函数,可以证明:
引理1 令参数 p , γ , c , α p, \gamma, c, \alpha p,γ,c,α 满足条件 p ≥ 3 L f , γ ≥ 0 , c < 1 / ( L f + γ σ max 2 ( A ) + p ) , α < c ( p − L f ) 2 4 σ max 2 ( A ) p \geq 3L_f, \quad \gamma \geq 0, \quad c<1/(L_f + \gamma\sigma^2_{\max}(A) + p), \quad \alpha < \frac{c(p-L_f)^2}{4\sigma^2_{\max}(A)} p≥3Lf,γ≥0,c<1/(Lf+γσmax2(A)+p),α<4σmax2(A)c(p−Lf)2.此时存在 β ′ > 0 \beta' >0 β′>0,使得对任意的 β ≤ β ′ \beta\leq\beta' β≤β′ 都有
ϕ t − ϕ t + 1 ≥ 1 8 c ∥ x t − x t + 1 ∥ 2 + α 2 ∥ A x ( y t + 1 , z t ) − b ∥ 2 + p 6 β ∥ z t − z t + 1 ∥ 2 . ( 3 ) \phi^t-\phi^{t+1} \geq \frac{1}{8 c}\left\|x^t-x^{t+1}\right\|^2+\frac{\alpha}{2}\left\|A x\left(y^{t+1}, z^t\right)-b\right\|^2+\frac{p}{6 \beta}\left\|z^t-z^{t+1}\right\|^2.\quad \quad \quad (3) ϕt−ϕt+1≥8c1 xt−xt+1 2+2α Ax(yt+1,zt)−b 2+6βp zt−zt+1 2.(3)
引理的证明过程主要分为三个部分:
(1) 在一定的参数条件下,分别估计 K ( x t , z t ; y t ) − K ( x t + 1 , z t + 1 ; y t + 1 ) K(x^t,z^t;y^t)-K(x^{t+1},z^{t+1};y^{t+1}) K(xt,zt;yt)−K(xt+1,zt+1;yt+1), d ( y t + 1 , z t + 1 ) − d ( y t , z t ) d(y^{t+1},z^{t+1})-d(y^t,z^t) d(yt+1,zt+1)−d(yt,zt)和 P ( z t ) − P ( z t + 1 ) P(z^t)-P(z^{t+1}) P(zt)−P(zt+1) 的下界表达式,从而得到 ϕ t − ϕ t + 1 \phi^t - \phi^{t+1} ϕt−ϕt+1 的下界;
(2) 通过原始误差界(Primal Error Bound)的相关结论,结合平方差公式、柯西-施瓦茨公式等简单的运算,将 ϕ t − ϕ t + 1 \phi^t - \phi^{t+1} ϕt−ϕt+1 的下界进行放缩,得到一个新的下界,它可以被写作几个(带有系数的)范数平方项的代数和(不妨记作 A + B + C − D A+B+C-D A+B+C−D);
(3) 根据对偶误差界(Dual Error Bound)的相关理论,我们可以提出一些条件并进行分类讨论:(i) 如果条件成立,则可通过对偶误差界的结论证明 B ≥ 2 D B \geq 2D B≥2D ; (ii) 如果条件不成立,那么利用具体不成立的条件可证明 A , B , C A, B, C A,B,C 中的某一项大于等于 2 D 2D 2D. 总之可证明 ( A + B + C ) / 2 (A+B+C)/2 (A+B+C)/2 是 ϕ t − ϕ t + 1 \phi^t - \phi^{t+1} ϕt−ϕt+1 的一个下界,具体表达式如公式(3)所示.
利用势能函数的充分下降,可以证明算法具有 O ( 1 / ϵ 2 ) O(1/\epsilon^2) O(1/ϵ2) 的迭代复杂度.
定理1 记 { ( x t , y t ) } \{(x^t,y^t)\} {(xt,yt)} 为本文中算法所生成的迭代序列. 如果上一节的两个假设成立,且参数 p , γ , c , α p, \gamma, c, \alpha p,γ,c,α 满足 p ≥ 3 L f , γ ≥ 0 , c < 1 / ( L f + γ σ max 2 ( A ) + p ) , α < c ( p − L f ) 2 4 σ max 2 ( A ) , p \geq 3L_f, \quad \gamma \geq 0, \quad c<1/(L_f + \gamma\sigma^2_{\max}(A) + p), \quad \alpha < \frac{c(p-L_f)^2}{4\sigma^2_{\max}(A)}, p≥3Lf,γ≥0,c<1/(Lf+γσmax2(A)+p),α<4σmax2(A)c(p−Lf)2, 此时存在 β ′ > 0 \beta' >0 β′>0, 使得对任意的 β ≤ β ′ \beta\leq\beta' β≤β′ 都有以下结论成立:
(1) { ( x t , y t ) } \{(x^t,y^t)\} {(xt,yt)} 的每一个聚点都是问题 (1) 的 KKT 点;
(2) 对于 ϵ > 0 \epsilon >0 ϵ>0,算法能在 O ( 1 / ϵ 2 ) O(1/\epsilon^2) O(1/ϵ2) 次迭代中找到一个 ϵ \epsilon ϵ-稳定点.
对于 h i ( i = m + 1 , ⋯ , m + l ) h_i ~(i=m+1, \cdots, m+l) hi (i=m+1,⋯,m+l) 都是线性函数的情形,对应的定理证明已在 [2] 中给出. 更进一步,本文给出了如下证明:
(1) 可证明 f ‾ \underline{f} f是 { ϕ t } \{\phi^t\} {ϕt} 的一个下界 [ 3 ] ^{[3]} [3]. 结合引理1以及算法框架,可得
lim t → ∞ ∥ ( x t + 1 , y t + 1 , z t + 1 ) − ( x t , y t , z t ) ∥ = 0. \lim\limits_{t\to\infty}\|(x^{t+1},y^{t+1},z^{t+1})-(x^t,y^t,z^t)\| = 0. t→∞lim∥(xt+1,yt+1,zt+1)−(xt,yt,zt)∥=0.
定义 F ( x , y , z ) = ( x + , y + , z + ) F(x,y,z) = (x^+,y^+,z^+) F(x,y,z)=(x+,y+,z+),其中 ( x + , y + , z + ) (x^+,y^+,z^+) (x+,y+,z+) 表示由算法生成的下一个迭代点. 由上式和 F F F 的连续性,可证明 { ( x t , y t , z t ) } \{(x^t,y^t,z^t)\} {(xt,yt,zt)} 的任意聚点 ( x ˉ , y ˉ , z ˉ ) (\bar{x},\bar{y},\bar{z}) (xˉ,yˉ,zˉ) 都是 F F F 的不动点,这说明 ( x ˉ , y ˉ ) (\bar{x},\bar{y}) (xˉ,yˉ) 是问题 (1) 的稳定点.
(2) 根据 ϕ t ≥ f ‾ \phi^t \geq \underline{f} ϕt≥f,可知对任意的 t > 0 t>0 t>0,存在 s ∈ { 0 , ⋯ , t − 1 } s \in \{0,\cdots,t-1\} s∈{0,⋯,t−1} 使得 ϕ s − ϕ s + 1 ≤ ( ϕ 0 − f ‾ ) / t . \phi^s - \phi^{s+1} \leq (\phi^0-\underline{f})/t. ϕs−ϕs+1≤(ϕ0−f)/t. 结合公式 (3) 可得 ∥ x s − x s + 1 ∥ 2 < C / t , ∥ A x ( y s + 1 , z s ) − b ∥ 2 < C / t , ∥ x s + 1 − z s ∥ 2 < C / t , ( 4 ) \left\|x^s-x^{s+1}\right\|^2
其中 C C C 是适当的常数.
一方面,根据公式 (4) 以及原始误差界的理论可证明 ∥ A x s + 1 − b ∥ ≤ B 1 C / t \|Ax^{s+1}-b\|\leq\sqrt{B_1 C}/\sqrt{t} ∥Axs+1−b∥≤B1C/t,其中 B 1 B_1 B1 是适当的常数. 另一方面,根据算法具有性质
x s + 1 = arg min x { ⟨ ∇ x K ( x s , z s ; y s + 1 ) , x − x s ⟩ + 1 c ∥ x − x s ∥ 2 + ι ( x ) } , x^{s+1}=\arg \min _x\left\{\left\langle\nabla_x K\left(x^s, z^s ; y^{s+1}\right), x-x^s\right\rangle+\frac{1}{c}\left\|x-x^s\right\|^2+\iota(x)\right\}, xs+1=argxmin{⟨∇xK(xs,zs;ys+1),x−xs⟩+c1∥x−xs∥2+ι(x)},
可以借此找出一个 v v v满足 v ∈ ∇ f ( x s + 1 ) + A T y s + 1 + ∂ ( ι ( x s + 1 ) ) v \in \nabla f\left(x^{s+1}\right)+A^T y^{s+1}+\partial\left(\iota\left(x^{s+1}\right)\right) v∈∇f(xs+1)+ATys+1+∂(ι(xs+1));对 v v v表达式中的各项进行放缩,最终可得 ∥ v ∥ ≤ B 2 C / t \|v\| \leq \sqrt{B_2C}/\sqrt{t} ∥v∥≤B2C/t,其中 B 2 B_2 B2 是适当的常数. 因此可以看出 ( x s + 1 , y s + 1 ) (x^{s+1},y^{s+1}) (xs+1,ys+1) 是问题 (1) 的一个 ( B / t ) (\sqrt{B}/\sqrt{t}) (B/t)-稳定点,其中 B = C max { B 1 , B 2 } B = C\max\{B_1,B_2\} B=Cmax{B1,B2}. 收敛率即得证.
3.3 分块优化
考虑分块优化问题
min f ( x 1 , x 2 , ⋯ , x N ) s.t. ∑ i = 1 N A i x i = b , x i ∈ X i , ( 5 ) \begin{aligned} & \min ~ f(x_1,x_2,\cdots,x_N) \\ \text{s.t.~} & \sum_{i=1}^N A_ix_i = b, ~x_i \in \mathcal{X}_i, \end{aligned} \quad \quad \quad \quad\quad \quad \quad \quad \quad \quad \quad\quad\quad (5) s.t. min f(x1,x2,⋯,xN)i=1∑NAixi=b, xi∈Xi,(5)
其中 X i \mathcal{X}_i Xi均为紧凸集. 定义 x t ( i ) = ( x 1 t + 1 , x 2 t + 1 , ⋯ , x i − 1 t + 1 , x i t , ⋯ , x N t ) x^t(i)=\left(x_1^{t+1}, x_2^{t+1}, \cdots, x_{i-1}^{t+1}, x_i^t, \cdots, x_N^t\right) xt(i)=(x1t+1,x2t+1,⋯,xi−1t+1,xit,⋯,xNt),并用 P X i ( ⋅ ) P_{\mathcal{X}_i}(\cdot) PXi(⋅) 表示到 X i \mathcal{X}_i Xi 的投影.
根据 2.2 节的算法,我们可以提出适合问题 (5) 的算法框架,并对其证明与定理1相同的收敛性结论. 在具体证明过程上,它与定理1的不同之处在于:(i) 在引理证明的第(1)步中,关于 K ( x t , z t ; y t ) − K ( x t + 1 , z t + 1 ; y t + 1 ) K(x^t,z^t;y^t)-K(x^{t+1},z^{t+1};y^{t+1}) K(xt,zt;yt)−K(xt+1,zt+1;yt+1) 下界的证明不同;(ii) 对于部分原始误差界结论的证明不同. 具体算法框架如下:
4. 数值实验
考虑问题
min x f ( x ) : = 1 2 x T Q x + r T x s.t. A x = b , ∥ x ∥ ≤ c , \min_x f(x) := \frac{1}{2}x^T Q x + r^T x \quad \text{s.t.~} Ax=b,~ \|x\|\leq c, xminf(x):=21xTQx+rTxs.t. Ax=b, ∥x∥≤c,
其中 Q ∈ R n × n Q \in \mathbb{R}^{n \times n} Q∈Rn×n 是对称而未必半正定的矩阵, r ∈ R n r\in\mathbb{R}^n r∈Rn, A ∈ R m × n A\in\mathbb{R}^{m\times n} A∈Rm×n, b ∈ R m b\in\mathbb{R}^m b∈Rm且 c > 0 c>0 c>0.
定义 X = { x ∣ ∥ x ∥ ≤ c } \mathcal{X} = \{x ~|~ \|x\|\leq c\} X={x ∣ ∥x∥≤c} 以及它对应的指示函数 ι ( ⋅ ) \iota(\cdot) ι(⋅). 对任意的 ( x , y ) (x,y) (x,y),可以找到 ∇ f ( x ) + A T y + ∂ ι ( x ) \nabla f(x) + A^T y + \partial \iota(x) ∇f(x)+ATy+∂ι(x) 中范数最小的元素,不妨记作 v v v. 结合 ϵ \epsilon ϵ-稳定点的定义,本节以 ∥ v ∥ + ∥ A x − b ∥ \|v\| + \|Ax-b\| ∥v∥+∥Ax−b∥ 的大小来衡量 x x x 与稳定点的距离.
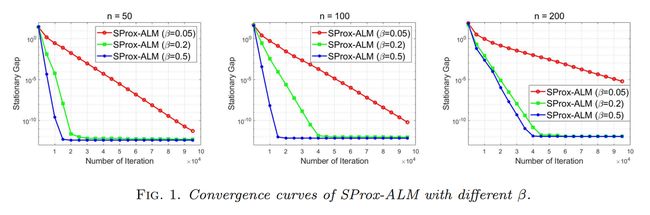
首先考察参数对本文算法的影响. 取 m = 20 m=20 m=20, n = { 50 , 100 , 200 } n = \{50,100,200\} n={50,100,200},固定的 p , γ , c , α p,\gamma,c,\alpha p,γ,c,α 及 β = { 0.05 , 0.2 , 0.5 } . \beta = \{0.05,0.2,0.5\}. β={0.05,0.2,0.5}.结果显示,对于不同规模的问题,较大的 β \beta β 值都有助于算法的收敛.
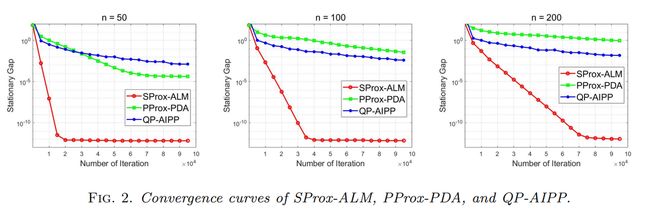
接下来将本文算法与其他方法进行比较. 在先前参数选择的基础上,固定 β = 0.2 \beta = 0.2 β=0.2. 将本文算法(SProx-ALM)、Pprox-PDA 算法 [ 4 ] ^{[4]} [4](Perturbed Proximal Primal-dual Algorithm)和 QP-AIPP 算法 [ 5 ] ^{[5]} [5](Quadratic Penalty Accelerated Inexact Proximal Point Method)进行比较. 结果显示,本文算法在 QP 问题的求解上具有更快的收敛速度.
参考文献
- Zhang, Jiawei, Wenqiang Pu and Zhi-Quan Tom Luo. “On the Iteration Complexity of Smoothed Proximal ALM for Nonconvex Optimization Problem with Convex Constraints.” (2022).
- Zhang, Jiawei and Zhi-Quan Tom Luo. “A Global Dual Error Bound and Its Application to the Analysis of Linearly Constrained Nonconvex Optimization.” SIAM J. Optim. 32 (2022): 2319-2346.
- Zhang, Jiawei and Zhi-Quan Tom Luo. “A Proximal Alternating Direction Method of Multiplier for Linearly Constrained Nonconvex Minimization.” SIAM J. Optim. 30 (2018): 2272-2302.
- Hajinezhad, Davood and Mingyi Hong. “Perturbed proximal primal–dual algorithm for nonconvex nonsmooth optimization.” Mathematical Programming 176 (2019): 207 - 245.
- Kong, Weiwei, Jefferson G. Melo and Renato D. C. Monteiro. “Complexity of a Quadratic Penalty Accelerated Inexact Proximal Point Method for Solving Linearly Constrained Nonconvex Composite Programs.” SIAM J. Optim. 29 (2018): 2566-2593.