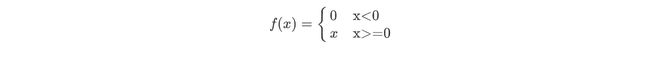常用激活函数代码+图像
![]()
文章目录
- 常见激活函数
-
- 1.ReLu函数
- 2.Sigmoid函数
- 3.tanh函数
- 4.总结
常见激活函数
如下图所示,在神经元中,输入的 inputs 通过加权,求和后,还被作用了一个函数,这个函数就是激活函数。引入激活函数是为了增加神经网络模型的非线性。没有激活函数的每层都相当于矩阵相乘。就算你叠加了若干层之后,无非还是个矩阵相乘罢了。
%matplotlib inline
import torch
import numpy as np
import matplotlib.pylab as plt
import sys
sys.path.append('..')
import d21zh_pytorch as d21
#绘制图形
def xyplot(x_vals,y_vals,name):
d21.set_figsize(figsize=(10,8))
d21.plt.plot(x_vals.detach().numpy(),y_vals.detach().numpy(),color='red')
d21.plt.tick_params(axis='x',colors='white',size=10,labelsize=20)#labelsize=20设置刻度字体大小
d21.plt.tick_params(axis='y',colors='white',size=10,labelsize=20)#labelsize=20设置刻度字体大小
d21.plt.xlabel('x',color='white',fontdict={'size':20})#设置标签的字体大小
d21.plt.ylabel(name+'(x)',color='white',fontdict={'size':20})#设置标签的字体大小
点我了解matplotlib—pyplot和pylab区别
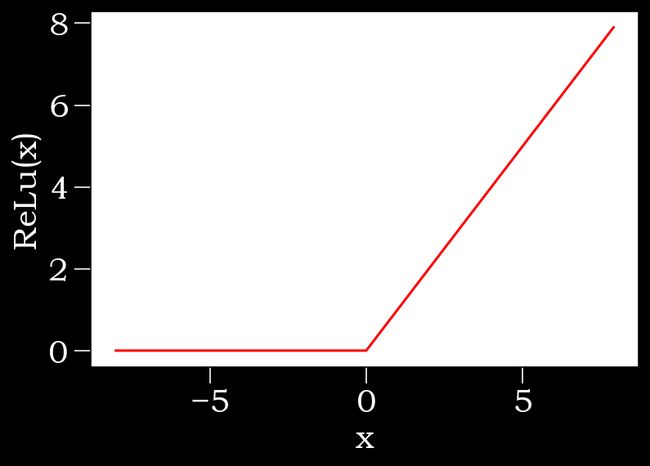
1.ReLu函数
Relu激活函数(The Rectified Linear Unit),用于隐层神经元输出。公式:
f ( x ) = m a x ( 0 , x ) f(x)=max(0,x) f(x)=max(0,x)即
x=torch.arange(-8.0,8.0,0.1,requires_grad=True)
y=x.relu()
xyplot(x,y,'ReLu')
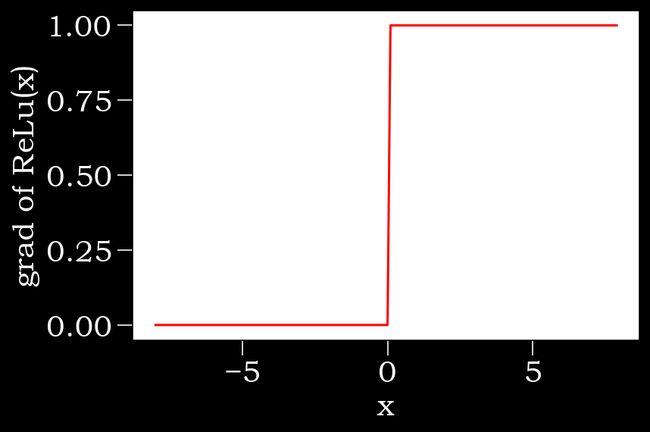
#ReLu函数的导数
y.sum().backward()
xyplot(x,x.grad,'grad of ReLu')
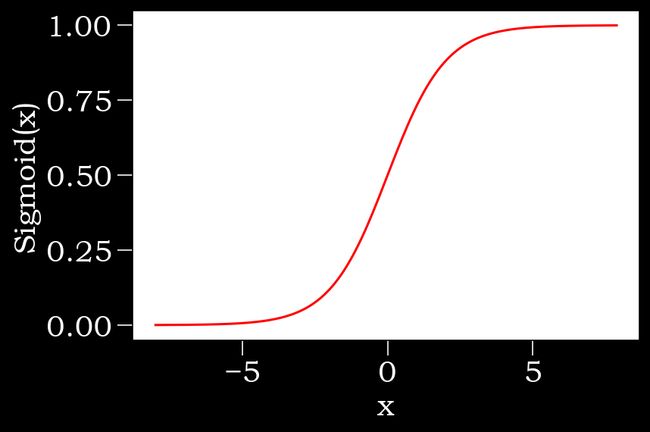
2.Sigmoid函数
Sigmoid它能够把输入的连续实值变换为0和1之间的输出,特别的,如果是非常大的负数,那么输出就是0;如果是非常大的正数,输出就是1,公式如下:
s i g m o i d ( x ) = 1 1 + e − x sigmoid(x)=\frac{1}{1+e^{-x}} sigmoid(x)=1+e−x1
y=x.sigmoid()
xyplot(x,y,'Sigmoid')
#Sigmoid函数的导数
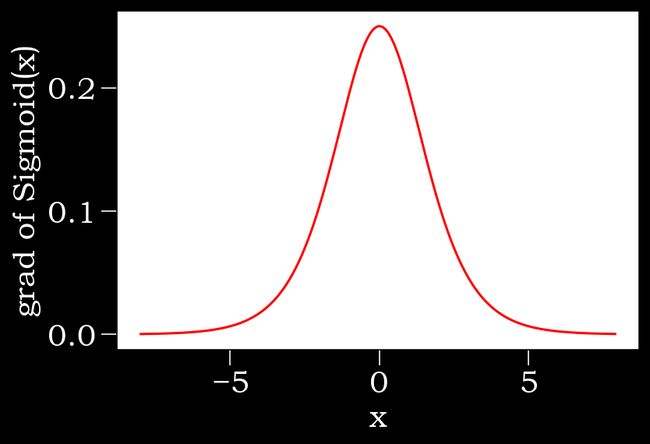
#当输入接近0时,Sigmoid函数的导数达到最大值0.25;当输入偏离0时,Sigmoid函数的倒数接近0
x.grad.zero_()#清除前面函数的梯度,梯度归零
y.sum().backward()
xyplot(x,x.grad,'grad of Sigmoid')
3.tanh函数
tanh读作Hyperbolic Tangent,它解决了Sigmoid函数的不是zero-centered输出问题。这两个函数之间的⼀个差异就是tanh 神经元的输出的值域是(-1; 1) ⽽⾮(0; 1)。这意味着如果你构建基于tanh 神经元,你可能需要正规化最终的输出(取决于应⽤的细节,还有你的输⼊),跟sigmoid ⽹络略微不同。当输入接近0时,tanh函数接近线性变换。虽然形状和Sigmoid函数的形状很像,但tanh函数在坐标系原点对称。公式如下:
t a n h ( x ) = 1 − e − 2 x 1 + e − 2 x tanh(x)=\frac{1-e^{-2x}}{1+e^{-2x}} tanh(x)=1+e−2x1−e−2x
y=x.tanh()
xyplot(x,y,'tanh')
#tanh函数的导数
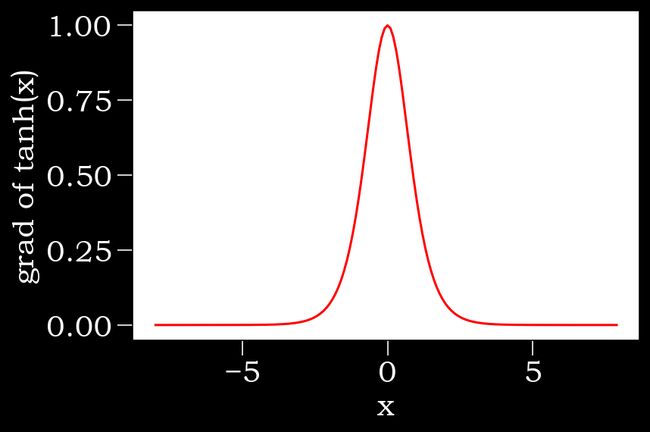
#当输入为0时,tanh函数的导数达到最大值1;当输入偏离0时,tanh函数的导数越接近0.
x.grad.zero_()#清除前面函数的梯度,梯度归零
y.sum().backward()
xyplot(x,x.grad,'grad of tanh')
4.总结
各种激活函数,有其各自的适用范围与优缺点。具体比较信息可参考此篇博客:常用激活函数(激励函数)理解与总结