紫书第6章 数据结构基础 例题（E-H)

H-Tree

Description
You are to determine the value of the leaf node in a given binary tree that is the terminal node of a path of least value from the root of the binary tree to any leaf. The value of a path is the sum of values of nodes along that path.

Input
The input file will contain a description of the binary tree given as the inorder and postorder traversal sequences of that tree. Your program will read two line (until end of file) from the input file. The first line will contain the sequence of values associated with an inorder traversal of the tree and the second line will contain the sequence of values associated with a postorder traversal of the tree. All values will be greater than zero and less than 500. You may assume that no binary tree will have more than 25 nodes or less than 1 node.

Output
For each tree description you should output the value of the leaf node of a path of least value. In the case of multiple paths of least value you may pick any of the appropiate terminal nodes.

Samples
Input
3 2 1 4 5 7 6
3 1 2 5 6 7 4
7 8 11 3 5 16 12 18
8 3 11 7 16 18 12 5
255
255
Output
1
3
255

题目大意
给出一个树的中根遍历顺序和后根遍历顺序
对树进行还原，求出从根节点出发到一个任意一个叶子节点路径的最小权值和
如果权值和相同，选择叶子节点值最小的那个
最后输出路径最小的这个叶子的节点值

思路分析
1.输入遍历顺序
2.根据顺序对树进行还原
3.搜索整个树

具体思路
中根遍历的顺序：左根右
后根遍历的顺序：左右根
所以我们针对一个大树，可以先在后根遍历中找到他的根
在后根遍历中找到根很简单，其实就是后根遍历的最后一个元素
然后在中根序列中找到刚才找到的这个根

根据中根序列：根的左边是左子树，右边是右子树
我们可以以根为分界线，不断的对中根遍历进行分裂
并且更新中根遍历，后根遍历。

这样不断的分离出左子树和右子树
然后用一对数组存储他们
lleft数组存储 根节点连接的左子树 的根 的权值
rright数组存储 根节点连接的右子树 的根 的权值

以上这些是建树的过程---------------

对于树的构建来说，不管是建树还是搜索树
很多时候都会用到递归或者dfs的思想

我们利用dfs搜索整个树，深度一直到树的叶子节点
在搜索到叶子节点时取一个最小的值即为答案

代码

#include
using namespace std;
const int maxn=1e4+10;//110
int zhong[maxn],hou[maxn],lleft[maxn],rright[maxn];
int n;
int sum;
int ans;
bool input(int *a)
{
	string t;//255
	if(!getline(cin,t))
	return 0;
	n=1;//1
	stringstream ss(t);
    while(ss>>a[n]) 
	n++;//2

    return n>1;
}
int build(int l1,int r1,int l2,int r2)
{
	if(l1>r1)
	return 0;
	int root=hou[r2];
	int p=l1;
	while(zhong[p]!=root)
	p++;
	
	int cnt=p-l1;
	
	lleft[root]=build(l1,p-1,l2,l2+cnt-1);
	rright[root]=build(p+1,r1,l2+cnt,r2-1);
	return root;
}
void dfs(int x,int ssum)
{
	ssum+=x;
	if(lleft[x]==0&&rright[x]==0)
	{
		if(ssum

难度偏高
抬走！下一题！

G-Trees on the level

Description
Trees are fundamental in many branches of computer science (Pun definitely intended). Current stateof- the art parallel computers such as Thinking Machines’ CM-5 are based on fat trees. Quad- and octal-trees are fundamental to many algorithms in computer graphics.

This problem involves building and traversing binary trees.

Given a sequence of binary trees, you are to write a program that prints a level-order traversal of each tree. In this problem each node of a binary tree contains a positive integer and all binary trees have have fewer than 256 nodes.

In a level-order traversal of a tree, the data in all nodes at a given level are printed in left-to-right order and all nodes at level k are printed before all nodes at level k + 1.

For example, a level order traversal of the tree on the right is: 5, 4, 8, 11, 13, 4, 7, 2, 1.

In this problem a binary tree is specified by a sequence of pairs ‘(n,s)’ where n is the value at the node whose path from the root is given by the string s. A path is given be a sequence of ‘L’s and ‘R’s where ‘L’ indicates a left branch and ‘R’ indicates a right branch. In the tree diagrammed above, the node containing 13 is specified by (13,RL), and the node containing 2 is specified by (2,LLR). The root node is specified by (5,) where the empty string indicates the path from the root to itself. A binary tree is considered to be completely specified if every node on all root-to-node paths in the tree is given a value exactly once.

input
The input is a sequence of binary trees specified as described above. Each tree in a sequence consists of several pairs ‘(n,s)’ as described above separated by whitespace. The last entry in each tree is ‘()’. No whitespace appears between left and right parentheses.

All nodes contain a positive integer. Every tree in the input will consist of at least one node and no more than 256 nodes. Input is terminated by end-of-file.

Output
For each completely specified binary tree in the input file, the level order traversal of that tree should be printed. If a tree is not completely specified, i.e., some node in the tree is NOT given a value or a node is given a value more than once, then the string ‘not complete’ should be printed.

Samples
Input
(11,LL) (7,LLL) (8,R)
(5,) (4,L) (13,RL) (2,LLR) (1,RRR) (4,RR) ()
(3,L) (4,R) ()
Output
5 4 8 11 13 4 7 2 1
not complete

题目大意
给出二叉树中所有节点的权值，和该节点从根节点出发的路径
一组数据输入完毕时后跟一个 “（）”作为结束标志
首先判断是否是一个正确的二叉树，每个节点是否只出现过一次
如果该二叉树合法，从上到下，从左到右输出他的每个节点的权值！

具体思路
首先，这个题很有好的给出了每个节点的路径
并且要求输出是从上到下，从左到右
此时我们可以很容易的想到字典序排序
L 在长度不一样的情况下，先输出长度小的
长度一样，先输出字典序小的那个

配合字典序排序，我们利用结构体存储每个节点
利用x表示 权值
利用y表示 路径长度-（其实不存也行，但是看着方便）

利用s表示 路径字符串

然后对于每个“（）”前的字符串，都对其进行拆解处理
分离出其中的x,y,s。并且用map数组记录字符串出现的次数
避免一个路径出现超过一次，

在输入“（）”时，对结构体机进行cmp排序，排序完之后进行
正确性检验：
首先检验在之前的输入中每个字符串是否只出现了一次
然后检验根节点的路径字符串长度是不是0
然后利用map数组对每个结构体点进行检验，检验除了根节点的每个节点是否有父节点，如果他的路径减去最后一位就是他父节点的路径，利用map检查父节点路径检查父节点是否存在。

这些都没问题之后判断该二叉树合法，输出
然后初始化所有的数组，map.，以便下一次计算！

代码

#include
using namespace std;
struct Stu
{
	int x,y;//x表示值，y表示路径长度！ 
	string s;//表示路径！ 
}stu[10001];
bool cmp(Stu a,Stu b)//字典序排序！ 
{
	if(a.y==b.y)
	return a.smmap;
        int flag=0;
	string t;
	while(cin>>t)
	{
		int num[1001]={0};//记录答案的数组！ 
		if(t=="()")//代表所有小数据处理完毕！ 开始排字典序！ 
		{
			sort(stu,stu+n,cmp);
			if(flag==1||stu[0].y!=0)
			{
				printf("not complete\n");
			}
			else//开始判断每个小数据有没有一个正确的父节点！ 
			{
				for(int i=0;i0)
					{
					string s;
					int l=stu[i].y;
					l--;
					for(int j=0;j=2)
			{
				flag=1;
			}
			stu[n].y=x;
			n++;
		}	
	}
	return 0;
}

题目难度一般，比较好想
只是处理数据有点麻烦
抬走，下一题！

F- Dropping Balls

Description
A number of K balls are dropped one by one from the root of a fully binary tree structure FBT. Each time the ball being dropped first visits a non-terminal node. It then keeps moving down, either follows the path of the left subtree, or follows the path of the right subtree, until it stops at one of the leaf nodes of FBT. To determine a ball’s moving direction a flag is set up in every non-terminal node with two values, either false or true. Initially, all of the flags are false. When visiting a non-terminal node if the flag’s current value at this node is false, then the ball will first switch this flag’s value, i.e., from the false to the true, and then follow the left subtree of this node to keep moving down. Otherwise, it will also switch this flag’s value, i.e., from the true to the false, but will follow the right subtree of this node to keep moving down. Furthermore, all nodes of FBT are sequentially numbered, starting at 1 with nodes on depth 1, and then those on depth 2, and so on. Nodes on any depth are numbered from left to right.
For example, Fig. 1 represents a fully binary tree of maximum depth 4 with the node numbers 1, 2, 3, …, 15. Since all of the flags are initially set to be false, the first ball being dropped will switch flag’s values at node 1, node 2, and node 4 before it finally stops at position 8. The second ball being dropped will switch flag’s values at node 1, node 3, and node 6, and stop at position 12. Obviously, the third ball being dropped will switch flag’s values at node 1, node 2, and node 5 before it stops at position 10.

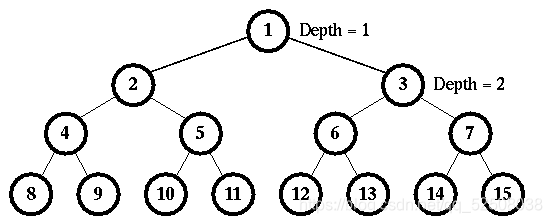
Now consider a number of test cases where two values will be given for each test. The first value is D, the maximum depth of FBT, and the second one is I, the Ith ball being dropped. You may assume the value of I will not exceed the total number of leaf nodes for the given FBT.

Please write a program to determine the stop position P for each test case.
For each test cases the range of two parameters D and I is as below:
2≤D≤20,and 1≤I≤524288

Input
Contains l+2 lines.

Line 1 I the number of test cases

Line 2 test case #1, two decimal numbers that are separated by one blank …

Line k+1 test case #k

Line l+1

test case #l

Line l+2−1 a constant -1 representing the end of the input file

Output
Contains l lines.

Line 1 the stop position P for the test case #1
…
Line k the stop position P for the test case #k …
Line l the stop position P for the test case #l

Samples
Input
5
4 2
3 4
10 1
2 2
8 128
-1
Output
12
7
512
3
255

题目大意
输入一个N，表示N个二叉树的滚球情况！
后面接N行，每行代表一个情况

题目背景：
有一个小球会从 根节点掉落
同时，二叉树的每个节点都有一个 1/0的值
当该节点的值为0时 ，球掉落到这个节点上，会先把这个节点的值从0改为1
然后从左边落下
当该节点为1时，球掉落到这个节点上，会先把这个节点的值从1改成0
然后从右边落下

接下来N行每行第一个数字表示 二叉树的层数
第二个数字表示 该球为掉落的第几个球

输出该球最后掉入的叶子节点编号

题目思路
这个题利用了二叉树的一些基本规律
利用这些规律解题就变得非常容易

如果父节点的编号是 i
那么他左子节点的编号就是 2 * i
右子节点的编号就是 2 * i+1

如果一个球 掉入入 父节点的次数是 i
那么这个球掉入他左子节点的 次数 是 （i+1）/2
掉入右子节点的次数是 i/2

利用这些规律，我们只需要每次判断小球掉入当前节点次数的奇偶，同时更新掉入当前节点次数的值和当前节点的值。

代码

#include
using namespace std;
int main()
{
	int n;
	while(cin>>n&&n!=-1)
	{
		for(int i=1;i<=n;i++)
		{
			int D,I;
			cin>>D>>I;//4 2
			int k=1;
			//1-3;
			for(int i=1;i

题目比较简单
抬走，下一题！

E-Self-Assembly

Description
Automatic Chemical Manufacturing is experimenting with a process called self-assembly. In this process, molecules with natural affinity for each other are mixed together in a solution and allowed to spontaneously assemble themselves into larger structures. But there is one problem: sometimes molecules assemble themselves into a structure of unbounded size, which gums up the machinery.

You must write a program to decide whether a given collection of molecules can be assembled into a structure of unbounded size. You should make two simplifying assumptions: 1) the problem is restricted to two dimensions, and 2) each molecule in the collection is represented as a square. The four edges of the square represent the surfaces on which the molecule can connect to other compatible molecules.

In each test case, you will be given a set of molecule descriptions. Each type of molecule is described by four two-character connector labels that indicate how its edges can connect to the edges of other molecules. There are two types of connector labels:

An uppercase letter (A, …, Z) followed by + or -. Two edges are compatible if their labels have the same letter but different signs. For example, A+ is compatible with A- but is not compatible with A+ or B-.
Two zero digits 00. An edge with this label is not compatible with any edge (not even with another edge labeled 00).
Assume there is an unlimited supply of molecules of each type, which may be rotated and reected. As the molecules assemble themselves into larger structures, the edges of two molecules may be adjacent to each other only if they are compatible. It is permitted for an edge, regardless of its connector label, to be connected to nothing (no adjacent molecule on that edge).

Figure A.1 shows an example of three molecule types and a structure of bounded size that can be assembled from them (other bounded structures are also possible with this set of molecules).

Input
The input consists of several test cases. A test case consists of two lines. The first contains an integer n (1≤n≤40000) indicating the number of molecule types. The second line contains n eight-character strings, each describing a single type of molecule, separated by single spaces. Each string consists of four two-character connector labels representing the four edges of the molecule in clockwise order.

Output

For each test case, display the word ‘unbounded’ if the set of molecule types can generate a structure of unbounded size. Otherwise, display the word ‘bounded’.

Samples
Input
3
A+00A+A+ 00B+D+A- B-C+00C+
1
K+K-Q+Q-
Output
bounded
unbounded

题目大意
先输入一个N表示正方形的种类数
每种正方形的个数是无限个

然后用一个字母 带一个 + 或 - 来标记 每个边
或者用00标记边

A+ 可以 和 A - 匹配 以此类推
00不能跟任何东西匹配

按顺时针的顺序输入正方形的四个边的 字母标记
输入N类这样的正方形
问这N类正方形是否能通过旋转，翻转，某种连接方式无限的延展
如果可以输出“unbounded”
如果不行输出“bounded”

思路
由于正方形数目不限，可以将正方形边上的符号看为点，正方形看做边，则可以根据正方形的边符号与符号的匹配规则构成一个有向图。则当且仅当途中存在有向环时有解。只需做一次拓扑排序即可。

思路2
由于本人不了解什么是拓扑排序
所以拓扑排序的方法没办法进行
查了一下：只要一个图有有向环的时候，这个图才可以无线延展下去
所以我们的任务就是查找是否存在有向环

1.输入每个方块的信息
2.创建2维数组，对他们进行编码，用二维数组表示两个节点的连接状态
3.对每个节点进行dfs操作，深度优先查找是否存在有向环！

注意事项
1.首先同组内的各各节点一定相连接的，把他们进行标记。

2.错位编码，区分+和-，在这里我们把+全部编码成偶数 -号全部编码成奇数
A+和 A-差1，利用异或操作，可以巧妙的找到跟自己相互补的节点的编码
一个数字跟1异或 ，如果是偶数 则+1，如果是奇数则 -1，所以我们这样编码可以巧妙的进行错位还能方便我们找到 跟自己互补的节点的编码

3.dfs，类似与双for循环暴力，每两个节点都进行一次查找，本着能走就走的原则进行dfs,如果发现这个两个节点之间相互联通并且在dfs的时候，发现又回到了自己，说明则产生了一个有向环，则证明可以无线延展。

代码

#include
using namespace std;
int g[52][52];//构建图的数组！
int vis[52];//相当于一个dfs的vis数组！
int ID(char a, char b) {
	if (b == '+') return (a - 'A') * 2;
	if (b == '-') return (a - 'A') * 2 + 1;
}
void connect(char a1, char a2, char b1, char b2) {
	//cout<>n&& n) {
		memset(g, 0, sizeof(g));
		while (n--) {
			char s[20];
			cin>>s;
			for (int i = 0; i < 4; i++) {
				for (int j = 0; j < 4; j++) {
					if (i != j && s[2*i]!='0' && s[2*j] != '0') {
						connect(s[2 * i], s[2 * i + 1], s[2 * j], s[2 * j + 1]);
					}
				}
			}
		}
		if (solve()) 
		puts("unbounded");
		else 
		puts("bounded");
	}
	return 0;
}