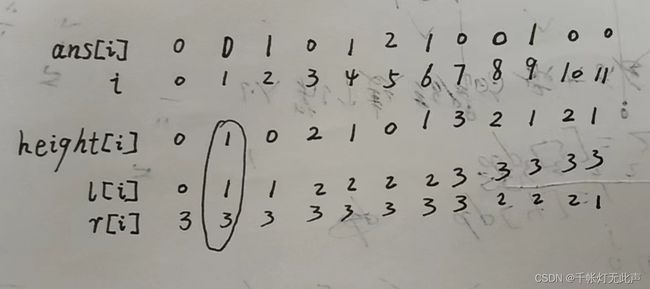力扣hot100 -- 双指针

目录

移动零

盛最多水的容器

三数之和

接雨水

前缀和 + 辅助数组

双指针

单调栈

---

移动零

283. 移动零 - 力扣（LeetCode）

关于swap

#include 
#include 
#include 

int main() {
    std::vector vec = {1, 2, 3, 4, 5, 6, 7};
    
    // 交换 vec 中第 1 个和第 7 个元素
    std::swap(vec[0], vec[6]);
    
    // 输出交换后的结果
    for (const auto &num : vec) {
        std::cout << num << " ";
    }
    std::cout << std::endl;

    return 0;
}

7 2 3 4 5 6 1

思路

i = 0, j = 0

为了保证 0 都在末尾，且顺序不变

i 指向 0 && j 指向 非0 元素时

交换两者（交换后，nums[x] <= i 都是非0元素； i < nums[x] <= j，都是 0）

坑

力扣核心代码模式，很容易越界，所以vector遍历时，要注意数组下标的问题 

AC  代码

O(n) 

class Solution {
public:
    void moveZeroes(vector& nums) {
        int i = 0, j = 0, n = nums.size();
        while (j < n && i < n) {
            if (!nums[i] && nums[j]) 
                swap(nums[i], nums[j]);
            if (nums[i] != 0) 
                i++; // 索引自增放后面，防止越界
            j++;
        }
    }
};

盛最多水的容器

11. 盛最多水的容器 - 力扣（LeetCode）

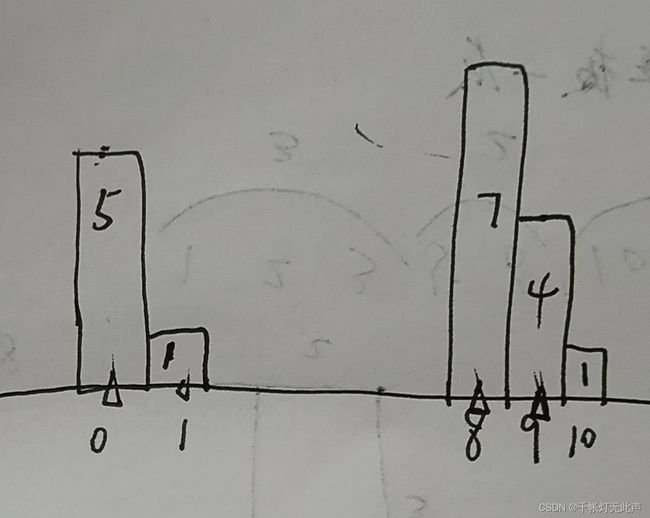
 i = 0, j = n - 1

ans = 距离 * 短板长度

所以，移动长板，距离变小，短板长度不可能变大，ans↓

只能移动短板

O(n) 

class Solution {
public:
    int maxArea(vector& height) {
        int ans = 0, n = height.size();
        int i = 0, j = n - 1;
        while (i < j) {
            int Min = min(height[i], height[j]); // 短板长度
            ans = max(ans, Min * (j - i));
            if (height[i] <= height[j]) i++;
            else j--;
        }
        return ans;
    }
};

三数之和

15. 三数之和 - 力扣（LeetCode）

思路

外层 for 遍历 i

内层 l, r 双指针

if( + +  == 0) 此时 l 和 r 都需要移动

否则，根据 > 0 或 < 0

只移动一个即可

坑

 关于去除重复解

1)
if (i > 0 && nums[i] == nums[i - 1])
    continue;

2)
while (l < r && nums[l] == nums[l + 1])
    l++; // 重复解
while (l < r && nums[r] == nums[r - 1])
    r--; // 重复解

1) 去掉下标 i 的重复解

2) 去掉下标 l, r 的重复解

AC  代码 

class Solution {
public:
    vector> threeSum(vector& nums) {
        if (nums.size() < 3) return {}; // 返回空数组

        vector > ans;
        sort(nums.begin(), nums.end()); // 排序

        int n = nums.size();
        for (int i = 0; i < n - 2; ++i) { // i l r
            if (nums[i] > 0) return ans; // 直接返回已有答案

            if (i > 0 && nums[i] == nums[i - 1])
                continue; // 去除重复解

            int l = i + 1, r = n - 1;

            while (l < r) { // 双指针循环判断

                if (nums[i] + nums[l] + nums[r] == 0) {
                    ans.push_back({nums[i], nums[l], nums[r]});
                    while (l < r && nums[l] == nums[l + 1])
                        l++; // 重复解
                    while (l < r && nums[r] == nums[r - 1])
                        r--; // 重复解
                    l++, r--; // 上面while结束后，还需要再移动一次
                }

                else if (nums[i] + nums[l] + nums[r] > 0)
                    r--;
                else
                    l++;
            }
        }
        return ans;
    }
};

接雨水

42. 接雨水 - 力扣（LeetCode）

前缀和 + 辅助数组

辅助数组 l[] 和 r[]

思路

每个柱子能盛水的高度，取决于左边最高和右边最高的柱子的短板

具体就是，min(l[i], r[i]) - h[i]

ans[] 可以省略，直接 res += ...

O(n) * 3

class Solution {
public:
    int trap(vector& h) {
        int n = h.size();
        // ans[] 某一根柱子上的雨水
        vector ans(n), l(n), r(n); // l[] 左边开始最高点, r[] 右边开始最高点
        
        l[0] = h[0], r[n - 1] = h[n - 1]; // 这里的赋值，需要以上面的分配空间为前提
        for (int i = 1; i < n; ++i) 
            l[i] = max(l[i - 1], h[i]); // 上一个l[]或当前h[] 取最大值
        for (int i = n - 2; i >= 0; --i)
            r[i] = max(r[i + 1], h[i]);

        // 对比 h[] 和 l[] / r[] 得到每个柱子接的雨水
        int res = 0;
        for (int i = 1; i < n - 1; ++i) // i==0 或 i==n-1，肯定没有雨水
            if (h[i] < l[i] && h[i] < r[i])
                res += min(l[i], r[i]) - h[i];
        
        return res;
    }
};

双指针

在  前缀和  思路的基础上，用两个指针 left, right 和两个变量 l_max, r_max ，代替两个辅助数组

优化空间复杂度 O(n) --> O(1)

补充解释

前缀和，是顺序遍历所有柱子

而双指针，是两个指针 left(顺序) 和 right(逆序)，双向同时向中间遍历

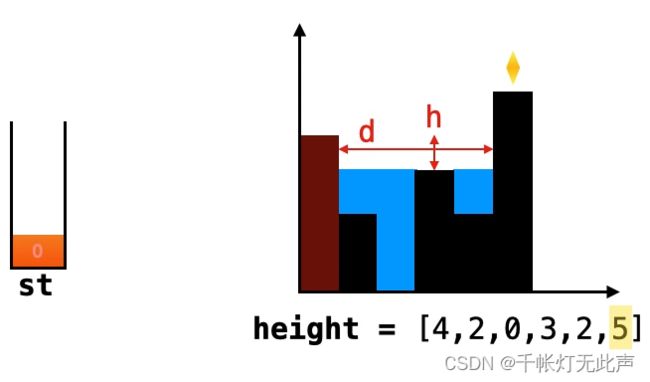
取较小那边的 max 值，用那边的 max 值，减去那边当前柱子的高度的 h[] 

为什么要选  较小  那边的来计算呢？（关键是  当前  两个字）

因为对于 当前的 left 或者 right 来说，较小那边的，一定是制约当前柱子雨水量的  短板

对照着理解下

AC  代码

O(n) * 1

class Solution {
public:
    int trap(vector& h) {
        int n = h.size(), res = 0;
        int l = 0, r = n - 1, l_max = 0, r_max = 0;
        while (l < r) { 
            l_max = max(h[l], l_max);
            r_max = max(h[r], r_max);
            // 注意 += 操作完后，对应一边的指针（l 或 r）要移动
            res += (l_max < r_max) ? (l_max - h[l++]) : (r_max - h[r--]); // 减去对应一边的柱子
        }
        return res;
    }
};

单调栈

简介

单调栈 - OI Wiki (oi-wiki.org)

模拟 

单调栈【基础算法精讲 26】_哔哩哔哩_bilibili

思路 

42. 接雨水 - 力扣（LeetCode）

力扣官方视频 -- 4'56开始看，13'56结束（9分钟）

关于代码中 st.pop() 以及 distance(积水宽度) 的计算 结合图理解

实际就是对单调栈的模拟，结合  += ( min(h1, h2) - h ) * 宽，即，(短板 - 当前) * 宽度 

过程

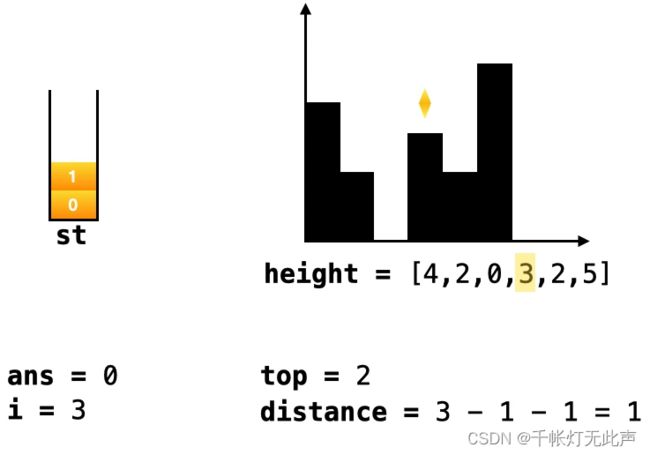
1）单调递减栈，储存可能形成 “低洼处” 的柱子

2）遇到更低的柱子，就插入 索引

3）遇到更高的柱子，意味着和前面 更低的，形成了低洼，就进入 内层 while 循环计算积水

4）被弹出的索引 top，h[top] 作为被积水的柱子高度，弹出栈顶后的新栈顶 left，作为 左端点

5）右端点即 当前 for 循环的 i， i - left - 1 即 积水宽度

6）高度取 当前高度 h[i] 和 左端点高度 h[left] 的 较小值

7）积水高度即，min( h[i], h[left] ) - h[top]

8）接着用积水 高度 * 宽度，即得到 += 的积水

9）while ( 栈非空 && 当前高度 h[i] > 栈顶高度 h[st.top()] ) ，重复 (3) ~ (8)

AC  代码

class Solution {
public:
    int trap(vector& h) {
        stack st; // 存储下标
        int n = h.size(), ans = 0;
        for (int i = 0; i < n; ++i) {
            while (!st.empty() && h[st.top()] < h[i]) { // 满足 低洼处 条件
                int top = st.top();
                st.pop(); // 弹出栈顶
                if (st.empty()) break; // 左边没有更高的柱子来形成积水

                int left = st.top();
                int height = min(h[i], h[left]) - h[top];
                int width = i - left - 1;

                ans += height * width;
            }
            // stack, queue 都是 push, vector 才是 push_back
            st.push(i); // 高度降低, 直接插入
        }
        return ans;
    }
};