python 基础知识点(蓝桥杯python科目个人复习计划33)
今日复习内容:以做题为主
例题1:小蓝的漆房
题目描述:
小蓝是一位有名的漆匠,他的朋友小桥有一个漆房,里面有一条长长的走廊,走廊两旁有许多相邻的房子,每间房子最初被涂上了一种颜色。
小桥来找小蓝,像让他把整个走廊都涂成一个颜色,小蓝告诉小桥,他每天只能涂一段长度为k的区间。对于每个区间,他可以选择将其中的房子重新涂上任何一种颜色,或者保持原来的颜色不变。
小桥想知道小蓝至少要涂几天,才能让整个走廊变得美丽。
请帮助小桥解决这个问题。
输入格式:
第一行包含一个整数t(1 <= t <= 100),表示测试用例的数量。
每个测试用例的第一行包含两个整数n和k(1 <= k <= n <= 10^4),第二行包含n个整数a1,a2,a3,...an(1 <= ai <= 60),表示每个房子最初的颜色。
保证所有的测试样例中n的总和不超过10^4。
输出格式:
对于每个测试用例,输出一个整数,表示小蓝需要涂漆的最少天数。
参考答案:
t = int(input()) # 测试用例的数量
for i in range(t):
n,k = map(int,input().split())
li = list(map(int,input().split()))
ans = 1e9 # 记录最终答案
for i in range(1,61):
cnt = 0 # 当前颜色的最小天数
j = 0
while j < n:
if li[j] != i:
cnt += 1
j += k
else:
j += 1
ans = min(ans,cnt)
print(ans)运行结果:
例题2:小蓝和小桥的挑战
题目描述:
小蓝和小桥是游戏世界里的两个好友,他们正在玩一个有趣的挑战,他们手中有一个长度为n的神秘物品序列,每个物品都有一个数字ai表示他们的价值。他们可以执行以下操作:
选择一个物品,并将其价值加1。
小蓝和小桥希望通过若干次操作使得这个序列的价值之和与价值的积都不为0。
请你帮他们计算,至少要执行多少次操作才能完成这个挑战。
输入格式:
第一行包含一个整数t(1 <= t <= 100),表示测试用例的数量。
接下来t行,每行包含两行数据,第一行为一个整数n(1 <= n <= 1000),表示物品的数量。第二行为n个整数a1,a2,...,an(-1000 <= ai <= 1000),表示初始的物品价值。
输出格式:
对于每个测试用例,输出一行一个整数,表示至少需要执行的操作次数。
参考答案:
t = int(input())
for i in range(t):
n = int(input())
li = list(map(int,input().split()))
s = 0
cnt = 0
for j in range(n):
if li[j] == 0:
cnt += 1
li[j] += 1
s += li[j]
if s == 0:
cnt += 1
print(cnt)运行结果:
例题3:DNA序列修正
题目描述:
在生物学中,DNA序列的相似性常被用来研究物种间的亲缘关系。现在我们有两条DNA序列,每条序列由A,T,C,G四种符号组成,长度相同。但是我们现在记录的DNA序列存在错误,为了严格满足DNA序列的碱基互补配对原则,即A-T和C-G,我们需要依据第一条DNA序列对第二条DNA序列进行以下操作:
1.选择第二条DNA序列的任意两个位置,交换它们的字符;
2.选择第二条DNA序列的任何一个位置,将其字符替换成A,G,C,T中的任意一个。
需要注意的是,每个位置上的碱基只能被操作一次。
你的任务是通过最小的操作次数,使第二条DNA序列和第一条DNA序列互补,并且已知初始两条DNA序列的长度是N。
输入格式:
第一行包含一个整数n(1 <= n <= 10^3) ,表示DNA序列的长度;
接下来的两行,每行包含一个长度为n的字符串,表示两条DNA序列。
输出格式:
输出一个整数,表示让第二条DNA序列和第一条DNA序列互补的最小操作次数。
参考答案:
x1 = {'A':'T','T':'A','C':'G','G':'C'}
n = int(input())
a = list(input())
b = list(input())
ans = 0
for i in range(n):
if x1[a[i]] != b[i]:
for j in range(i+1,n):
if x1[a[i]] == b[j] and x1[a[j]] == b[i]:
b[i],b[j] = b[j],b[i]
ans += 1
print(ans)运行结果:
例题4:无尽的石头
题目描述:
在一个古老的迷宫里,由一道无尽的通道,通道上每隔一定的距离就会有一块神秘的石头石头上刻着从1开始的连续整数。从1号石头开始,每块石头的编号都比前一块石头大1。
石头上的数字有特殊的意义。如果你站在编号为n的石头上,并向前走,你将会瞬间移动到编号为n + x的石头上,其中x为n的各数位之和。
例如,你站在编号为16的石头上,由于1 + 6 = 7,所以下一步你会移动到编号为16 + 7 = 23的石头上。
现在,会有多次询问,你需要对每个询问输出从1号石头出发,到达指定编号石头的的最少步数,如果无法到达,则输出-1。
输入格式:
输入包含一个整数t(1 <= t <= 100),表示有t个询问。
接下来t行,每行一个整数n(1 <= n <= 10^6),表示目标石头的编号。
输出格式:
对于每个询问,输出一行,表示从1号石头到达目标石头的最小步数。如果无法到达,输出-1。
参考答案:
stones = {} # key存放能走到哪块石头,value存放走到这块石头需要的步数
def pre():
x = 1
cnt = 0
while x <= 1e6:
stones[x] = cnt
x += sum(map(int,list(str(x))))
cnt += 1
pre()
t = int(input())
for i in range(t):
s = int(input())
if s in stones:
print(stones[s])
else:
print(-1)运行结果:
例题5:计算函数值
题目描述:
在一个神秘的世界中,存在一个传说中的神秘花园,被认为拥有无限的知识。但要进入这个花园,你必须解决花园入口处的一道神秘数学难题。这道难题与一个特殊的数学函数有关,称为“神秘函数”。
神秘函数S(x)的定义如下:
当x = 0 时,S(0) = 1;
当x为偶数时,S(x) = S(x/2);
当x为奇数时,S(x) = S(x - 1) + 1。
你需要编写一个程序,计算给定正整数x,神秘函数S(x)的值。只有当你正确解决了这道难题,才能获得通行证,进入神秘花园探索其中的神秘宝藏。
输入描述:
输入包含一个正整数x(1 <= x <= 10^6),表示你要解决的神秘函数问题。
输出描述:
输出一个整数,表示神秘函数S(x)的值,即你成功解决问题后得到的答案。
参考答案:
def S(x):
if x == 0:
return 1
elif x % 2 == 0:
return S(x / 2)
else:
return S(x - 1) + 1
t = int(input())
print(S(t))运行结果:
例题6:带分数
题目描述:
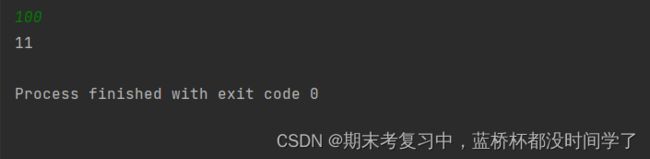
100可以表示为带分数的形式:100 = 3 + 69258 / 714
还可以表示为:100 = 82 + 3546 / 197
注意特征:带分数中,数字1到9分别出现且只出现一次(不包含0),
类似这样的带分数,100有11种表示法。
输入描述:
从标准输入读入一个正整数N(N < 1000 * 1000)。
输出描述:
程序输出该数字用数码1到9不重复不遗漏地组成带分数表示的全部种数。
注意:不要求输出每个表示,只统计有多少表示法!
参考答案:
n = int(input())
ans = 0 # 记录一共有几种答案
for st in itertools.permutations('123456789'):
st = ''.join(st)
for i in range(0,len(str(n))):
a = int(st[:i+1])
if a >= n:
break
bl = (n - a) * int(st[-1])%10 # b的最后一位
if bl == 0:
continue
b_ind = st.index(str(bl))
if b_ind <= i or b_ind >= 8:
continue
b = int(st[i+1:b_ind+1])
c = int(st[b_ind+1:])
if n == a + b/c:
ans += 1
print(ans)运行结果:
例题7:计票
题目描述:
学校对某建筑物征集命名。现在有N个候选名,有M个学生参与投票,每个学生只能投出一票。投票信息队列按学生投票时间先后顺序生成,系统按投票信息队列中的数据,按顺序依次处理每个投票。为了防止刷票,系统会记录投票时间(第几天,时,分,秒)。倘若现在处理的一个投票是在t时刻投票给x名字,系统会计算目前以t时刻为最后一秒的连续60秒内该名字的投票数(即若t为2分57秒,该60秒为从1分58秒开始),若得票数达到设定值K,则该名字在这60秒内的得票数永久清零,但是投票信息队列中系统还没有处理到的投票不会清零。给出投票队列,请你输出最终每个名字的得票数。
输入格式:
第一行输入为3个正整数N,M,K,含义如题目所述。
接下来M行,表示投票队列中的数据信息,每行5个整数d,h,m,s,x,分别表示第几天,时,分,秒投的票和投给的编号。
输出格式:
输出N行,每行一个数字,第i行表示编号为i的名字所得票数。
参考答案:
N,M,K = map(int,input().split())
date = [[0 for i in range(10 * 24 * 60 * 60)]for j in range(N+1)]
for i in range(M):
d,h,m,s,x = map(int,input().split())
tot = (d-1)*24*60*60 + m * 60 + s
date[x][tot] += 1
cnt = sum(date[x][max(0,tot - 60 + 1):tot + 1])
if cnt >= K:
for j in range(max(0,tot - 60 + 1),tot + 1):
date[x][j] = 0
for i in range(N+1):
print(sum(date[i]))
运行结果:
例题8:小蓝的数字
题目描述:
小蓝比较奇怪,他只对数字0和数字1感兴趣,给定一个正整数n,小蓝想知道数字1到n中有多少数字是仅由数字0和数字1组成的(包括数字1和n),请聪明的你帮小蓝计算一下吧。
输入描述:
输入仅包含一个正整数n,含义如上所示。
输出描述:
输出一个非负整数,表示答案。
参考答案:
n = int(input())
cnt = len(str(n)) # 统计n的位数
def dfs(d,value):
if d == cnt:
if n >= value >= 1:
return 1
else:
return 0
return dfs(d+1,value*10) + dfs(d+1,value*10 + 1)
print(dfs(0,0))运行结果:
OK,这篇就写到这里,下一篇继续!(感觉有点费命啊)