leetcode.78 子集

思路一：扩展法（暴力破解）

任何集合的子集都存在空集，取出原子集进行一一的扩展，如图所示，每一步结果子集的变化过程取出原有子集放入新建集合中（防止引用传递），将元素存入新集合构成新的子集，再将新的子集放入结果子集中【扩展结果子集】

这种解法适合不重复子集的情况（【1,2】【2,1】为相同子集）

代码实现如下：

class Solution {
    public List> subsets(int[] nums) {
        List> result=new ArrayList<>();
        result.add(new ArrayList());//初始化一个子集为空集
        for(int i:nums)
        {
            List> subset=new ArrayList<>();//二维数组，存放每一轮新加入的子集
            for(List list:result) //将新元素加入现有子集中
            {
        //创建一个新集合将子集存入，为了不改变原有的子集，防止引用传递，新元素的加入构成新的子集
                List temp=new ArrayList<>(list);
                temp.add(i);//扩展原子集
                subset.add(temp);//形成新的子集
            }
            for(List l:subset)    //将新的子集加入原有子集中
            {
                result.add(l);
            }
        }
        return result;
    }
}

时间复杂度 O(n^2)   ,空间O(n^2)  需要一个临时的二维数组

思路二：回溯

我把这个过程描述为，每次确定一个枝的深度（这里即子集的长度），由于空集已加入，枝的深度（子集长度）从1开始

当深度为1时，达到深度1开始回溯，如果1是枝，那么回溯就是后面的2、3剪枝，不再继续遍历，已经满足条件了

当深度为2时，达到深度2 开始回溯，3被剪枝，不再遍历

当深度为3时..............

迷宫的例子(重复回溯到上一步，尝试其它路径,只不过第一轮只走一步（子集元素个数为1）遍历有多少条路，第二轮走两步（子集元素个数为2）遍历有多少条路，第三轮（子集元素个数为3）遍历有多少条路)

代码如下：

注释版
class Solution {
    public List> subsets(int[] nums) {
    List> result = new ArrayList<>();//结果集
    result.add(new ArrayList());//加入空集
    for(int len=1;len<=nums.length;len++)//控制递归深度（这里是子集中的长度，即子集中有几个元素）
    {
        backTrack(nums,result,len,0,new ArrayList());//这个0看作是“迷宫每一次的入口”
    }
    return result;
    }
//回溯函数  为什么无返回值，因为子集已加入结果集，不需要返回值
//参数解释  每一个走过的“节点”从数组取，结果集，每一轮递归深度，每一轮起始，临时集合
    private void backTrack(int[] arrs, List> res,int length,int index,List subset)
    {
        if(subset.size()==length)//满足递归深度，加入子集
        {
            res.add(new ArrayList<>(subset));//创建一个新集合，防止引用传递，如果加入subset，最终返回的结果就都是空集，因为subset最终为[]
            return ;
        }
        for(int i=index;i

无注释

class Solution {
    public List> subsets(int[] nums) {
        List> result = new ArrayList<>();
        result.add(new ArrayList<>());
        for(int len=1;len<=nums.length;len++)
        {
            backTrack(nums,result,len,0,new ArrayList<>());
        }
        return result;
    }
    private void backTrack(int[] nums,List> result,int length,int index,List subset)
    {
        if(subset.size()==length)
        {
            result.add(new ArrayList(subset));
            return;
        }
        for(int i=index;i

 总结：思路捋清楚，代码就好写

*第二次写很快就写出来了，而且昨天不理解的点，好像一下就打开了

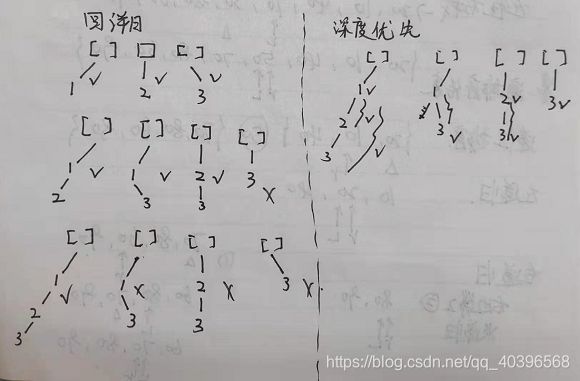
思路3：深度优先DFS 

打勾的地方是每一次加入的子集的顺序

代码实现如下：

class Solution {
    public List> subsets(int[] nums) {
        List> result = new  ArrayList<>();
        dfs(nums,result,0,new ArrayList<>());
        return result;
    }
    private void dfs(int[] arrs,List> res,int index, List subset)
    {
        res.add(new ArrayList<>(subset));//经过的每条路径都加入 结果集
        if(arrs.length==index)//到底了，无路可走，返回上一层
        {
            return;
        }
        for(int i=index;i

总结：深度优先，记录最开始的节点，然后记录走过的每一个节点，达到最大深度就不再走了，第二次写：没能完全写出来，但还是有了更多的理解，递归过程的变化也能一下子就想通了，没绕进去

回溯算法与 DFS 的区别就是有无状态重置 

回溯要重置，dfs不重置   可以看作回溯每次的进口一致（1），dfs不一致（1）（2）（3）