从0开始图形学（光栅化）

前言

        说起图形学，很多人就会提到OpenGL，但其实两者并不是同一个东西。引入了OpenGL加重了学习的难度和成本，使得一些原理并不直观。可能你知道向量，矩阵，纹理，重心坐标等概念，但就是不知道这些概念在图形学中具体是怎么使用的。

        本文不使用OpenGL，只用C代码实现光栅化过程，并配合OpenCV来显示渲染结果。让图形学的相关过程和原理变的直观和纯粹，本文结束后，我们将能够把一个3D模型文件只通过C语言渲染出来，如下结果。

环境准备

        首先需要安装开发环境，以Windows为例（Mac使用XCode，配置方法可以网上搜索）,开发工具首选Visual Studio。然后需要安装OpenCV环境，OpenCV在此只用来显示渲染结果，同时用到诸如画线和画点的简单功能，它不是必要的。参照Windows中安装OpenCV开发环境-CSDN博客

        完成开发环境搭建后，创建一个控制台项目，打开main函数所在的cpp文件，输入以下代码

// CGFromZero.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
//

#include 
#include 
#include 

const int gRstImgWid = 1000, gRstImgHei = 600;      // 结果图的长宽大小
unsigned char _rstImage[gRstImgHei][gRstImgWid][3]; // 结果图
const char _backColor[3] = {50, 100, 150};          // 结果图的背景颜色

void ShowCGRst()
{
    cv::Mat cvRst = cv::Mat(gRstImgHei, gRstImgWid, CV_8UC3);

    for (size_t y = 0; y < gRstImgHei; ++y)
    {
        for (size_t x = 0; x < gRstImgWid; ++x)
        {
            cvRst.data[y * cvRst.step + x * cvRst.channels() + 0] = _rstImage[y][x][2];     // 这里没有错，OpenCV中的数据存储顺序是BGR，而我们的数据顺序是RGB
            cvRst.data[y * cvRst.step + x * cvRst.channels() + 1] = _rstImage[y][x][1];
            cvRst.data[y * cvRst.step + x * cvRst.channels() + 2] = _rstImage[y][x][0];
        }
    }

    cv::imshow("愚 匠", cvRst);
    cv::imwrite("./Chapter0.png", cvRst);
    cv::waitKey(-1);
}

void CGRender()
{
}

int main()
{
    // 先将结果图画上背景色
    for (size_t y = 0; y < gRstImgHei; ++y)
    {
        for (size_t x = 0; x < gRstImgWid; ++x)
        {
            _rstImage[y][x][0] = _backColor[0];
            _rstImage[y][x][1] = _backColor[1];
            _rstImage[y][x][2] = _backColor[2];
        }
    }

    // 渲染
    CGRender();
    //
    // 显示渲染结果
    ShowCGRst();
}

        编译，运行，如果出现以下的图像，就说明环境准备就绪，我们后续的学习内容将在CGRender()这个函数上实现

第一章：从3D到2D

概念解说

        图形学渲染，就是将3D的东西“画”到2D的屏幕上，和拍照的效果是一样的，这也是为什么很多3D渲染引擎会有“相机”这个概念，这一节我们来看一下怎么把3D变成2D。

场景定义

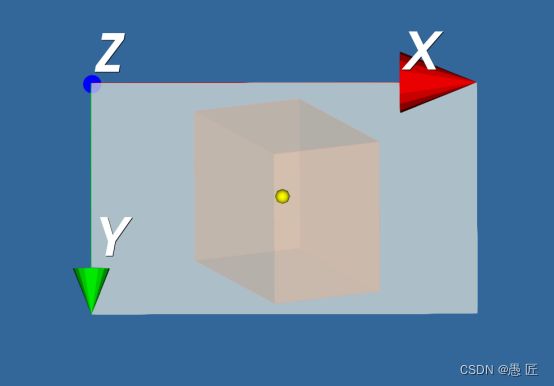
        首先，我们定义一个渲染场：一个定义好的坐标系中某个3D的箱子，黄色的球体代表相机，如下图所示

        我们的渲染结果就应该同相机视角看到的结果一样，如下图所示，透过半透明的“画布”，可以看到箱子在“画布”上的样子

问题提出

        那么，如何实现上面效果呢？我们先从箱子的整体轮廓入手，很简单，只要将箱子的八个顶点坐标的Z轴分量去掉，找到图片上对应的[X,Y]就是对应顶点的渲染位置（图中红色的点），再将点和点之间用线连接起来，也就是箱子的8条边（图中黄色的线）

是不是马上就有点立体感了！那代码上要怎么实现呢，很简单！

C核心代码

        首先，定义需要渲染的点，以及这些点的关系索引

// 定义渲染数据
float _points[8][3] =       // 点的数据
{
    {469.70839522142523, 181.86451044628149, 268.14698315693755}, // x, y, z
    {741.60073227608791, 149.05001503297740, 390.61234945175556},
    {741.60073227608791, 535.42034601093997, 494.13996576730500},
    {469.70839522142523, 568.23484142424411, 371.67459947248699},
    {258.39926772391209, 64.579653989059977, 705.86003423269506},
    {530.29160477857477, 31.765158575755891, 828.32540052751301},
    {530.29160477857477, 418.13548955371851, 931.85301684306251},
    {258.39926772391209, 450.94998496702260, 809.38765054824444},
};

int _planes[6][4] =      // 面的数据
{
    {0, 1, 2, 3},     // 每个面4个角的顶点对应于索引值
    {4, 5, 6, 7},
    {1, 5, 6, 2},
    {3, 2, 6, 7},
    {0, 4, 7, 3},
    {0, 1, 5, 4}
};

        第二步，根据上述的实现原理，将其画在结果图上，为方便，我们直接在ShowCGRst函数中对结果图进行修改，这里我们使用了OpenCV的画点函数cv::circle和画线函数cv::line

    // 将_points画到结果上
    int x, y, z;

    for (int i = 0; i < 8; ++i)
    {
        x = _points[i][0];
        y = _points[i][1];
        z = _points[i][2];
        cv::circle(cvRst, cv::Point(x, y), 5, cv::Scalar(0, 0, 255), -1);     // 使用OpenCV的画点函数
    }

    // 将点之间的关系（即箱子的边缘线）画出来
    int x1, y1, z1;

    for (int i = 0; i < 6; ++i)
    {
        for (int j = 0; j < 3; ++j)
        {
            x = _points[_planes[i][j]][0];
            y = _points[_planes[i][j]][1];
            z = _points[_planes[i][j]][2];
            x1 = _points[_planes[i][j + 1]][0];
            y1 = _points[_planes[i][j + 1]][1];
            z1 = _points[_planes[i][j + 1]][2];
            cv::line(cvRst, cv::Point(x, y), cv::Point(x1, y1), cv::Scalar(0, 255, 255), 2);
        }

        x = _points[_planes[i][0]][0];
        y = _points[_planes[i][0]][1];
        z = _points[_planes[i][0]][2];
        cv::line(cvRst, cv::Point(x, y), cv::Point(x1, y1), cv::Scalar(0, 255, 255), 2);
    }

下载完整代码

        这里已经画出了箱子的“骨”，下一步我们将绘制箱子的“皮”

第二章：三角面片及其填充

概念解说

        上一节中，我们画出了箱子的顶点和边缘线，箱子还只是一个骨架而已。这一节我们来将箱子的“皮”画出来，让箱子的形体更完整。

        首先，我们需要将箱子的面由四边形进一步切割成三角形，并进行填充。为什么要将其切割成三角形？原因大概有这么几个

        （1）三角形才是最简单的多边形，任何多边形都可以用三角形拼凑出来，或者说任何多边形都可以切割成多个三角形;

        （2）三角形能保证其面上所有的点都在同一个平面，其他形状就没有这个特性，例如将一张A4纸沿着对角线对折，它还是只有4条边，但是它就变成了两个三角面，而且这两个三角面不在同一个平面上；

        （3）绝大多数标准的3D数据都是由3角形构成，而且很多加载数据的软件一般都会提供将数据3角形化的接口！

数学计算

        下一步如何填充三角形呢？最关键的点就是如何判别一个点是否在一个3角形中。

        如下图，三角形ABC，任意点D，如果D在三角形内，则按顺序（如A->B->C）有：向量AB旋转到向量AD为逆时针，向量BC旋转到向量BD为逆时针，向量CA旋转到向量CD为逆时针，也就是说三个旋转的方向是一致的！而这个特性在数学上刚好有对应的表示方式----向量的叉乘

        向量的叉乘，简单来说就是两个向量、叉乘结果会生成另外一个向量，那么垂直于和组成的平面，而且的方向和旋转到的方向刚好对应！而且因为我们所有的操作都是在XY平面上，所以这里的得x和y分量都为0，其z分量就刚好表示这个方向。