3、计算机图形学——光栅化

简介

在进入具体的直线光栅化以及三角形光栅化算法之前，我们首先需要知道光栅化是一个什么样的过程。简单来说光栅化的目的就是将想要展现的物体给真正现实到屏幕上的过程，因为我们的物体其实都是一个个顶点数据来表示的，如何表这些蕴含几何信息的数据转化为屏幕上的像素就是光栅化所考虑的东西。比如说一条直线，究竟该用哪些像素点去逼近它，一个三角形，又用哪些像素集合表示它，这都是光栅化的过程。本节主要讨论介绍两个直线光栅化和一个三角形光栅化算法。

• 屏幕像素表示
  屏幕中的每一个像素点我们都用整数坐标进行表示，最大最小值与分辨率相对应，考虑到每个像素都有一定的面积，我们定义(x+0.5,y+0.5)为该(x,y)像素的中心，如图中黑圈所示
  

直线光栅化算法

DDA数值微分算法

DDA算法是一个非常简单直观的算法。
首先当任何一条直线知道任意两点时都可以用y = k x + b 来表示，其中k代表斜率，如果∣ k ∣ < 1，那么它的主要行进方向就是x轴，即x轴的变化要比y轴快，相反如果如果 |k| >1，那么它的主要行进方向就是y轴，即y轴的变化要比x轴快。如下图所示：

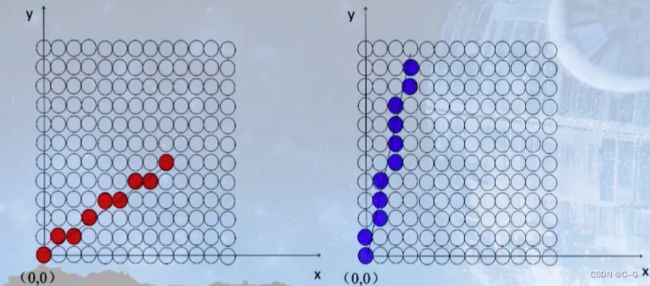
中点Bresenham算法

我们首先规定想要光栅化的线段的起点P 0 ( x 0 , y 0 )与终点P 1 ( x 1 , y 1 ),则该直线方程可以用y = kx + b的形式来表示，定义 f(x,y) = y - kx -b中点Bresenham算法的思想其实也比较简单，我们在这里只给出0 < k < 1 0

我们已经成功画出了前三个蓝色方格之后，所要考虑的便是第三个蓝色方格右边或者右上的橙色方格，此时我们取这两个橙色方格的中点，如图中圆圈符号所对应的那个点，倘若这个点在直线方程的下面，那么很明显我们应该选择右上的方格

第二种情况

此时中点位于直线方程的上方，此时选择右边的橙色方格。

至此，如何判断两种方格选择的条件已很明显，就是确定中点与直线的位置关系，这里就可以使用到一开始定义的f(x,y) = y - kx -b的方程了。

显然，当f(x+1,y+0.5) > 0的时候中点在直线上方，当f(x+1,y+0.5) < 0的时候中点在直线下方 （其中x+1，y+0.5是为了表示两个橙色方格的中点，此时x，y为前一个确定的像素坐标）

三角形光栅化算法

三角形是最基本的多边形，大部分的模型都是用一个个三角形面表示，且任意的其它多边形其实都可以转化成多个三角形的形式，因此三角形的光栅化可以说是图形学中最基础的部分了

其实有一个非常直观的做法，我们对屏幕中的每一个像素进行采样，如果这个像素点在三角形之中那么这个像素点就应该被采用！对，这其实就是该算法的做法。那么该如何去判断一个点在不在三角形内部呢，那么其中一种办法就是利用叉乘的性质了

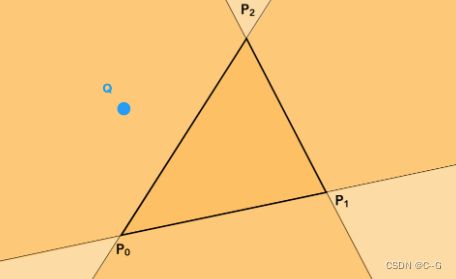
如图所示，我们事先知道想要光栅化的三角形的三个顶点P0，P1，P2，以及检测点Q。
只要分别计算P0P1P0Q，P1P2P1Q，P2P0*P2Q 如果三者同号则代表点P在三条线段的同一边，那么必然处于三角形内部，如果不同号则代表该点一定在三角形外部！

因此自然的，只需要遍历每一个点就可以得出三角形的光栅化结果了！当然我们还可以进一步的进行优化，因为显然并没有必要去测试屏幕中的每一个点，一个三角形面可能只占屏幕很小的部分，可以利用一个bouding box 包围住想要测试的三角形，只对该bounding box内的点进行采样测试，如下图：

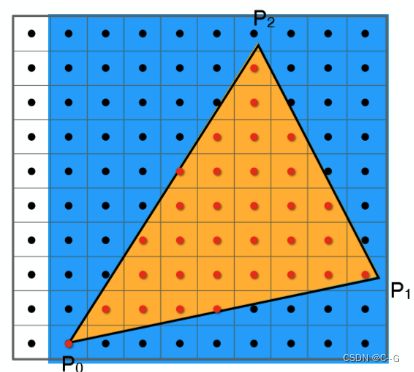
重心坐标

给定三角形的三点坐标A, B, C，该平面内一点(x,y)可以写成这三点坐标的线性组合形式，即 ( x , y ) = α A + β B + γ C (x,y) 且满足 α + β + γ = 1则称此时3个坐标A,B,C的权重α , β , γ 为点( x , y ) (x,y)(x,y)的重心坐标。

几何面积角度求解

重心坐标还有一个另外一个角度的等价定义

坐标系角度求解

针对重心坐标系的另外一种等价视角便是，以A点为原点，AB,AC分别为新的坐标系的单位向量构建坐标系，如图所示

其中给定任意点P的坐标可以用 β , γ \beta,\gammaβ,γ来表示，即P ( β , γ ) P(\beta,\gamma)P(β,γ),不难得出，P点坐标在原坐标系中的位置满足

到这里其实就可以发现，我们已经成功的把P用三角形的三个顶点的线性组合表示了，并且3个权重之和为1，完全符合定义，因此这是一种完全等价的角度

从这种角度出发，我们完全可以将上式表现成一个线性方程组来求解出β , γ \beta,\gammaβ,γ，两个未知量，两个式子，如下

重心坐标的运用

重心坐标在图形学中最重要的运用便是插值，他可以根据三个顶点A,B,C的属性插值出任意点的属性，无论是位置，颜色，深度，法线向量等等，而这些属性在之后的着色或是消除隐藏曲面都有很大的作用，光栅化三角行的具体运用，即判断一个点是否在三角形内，完全可以用本节的重心坐标是否都大于0来代替之前的叉乘(其实二者一定程度上是等价的)。利用该条件来进行sample 再判断是否画出该像素

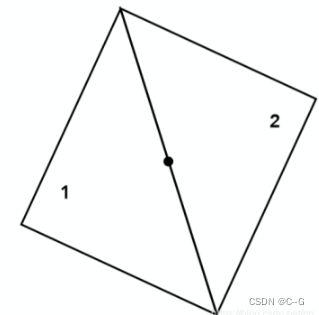
如果一个点正好处于两个三角形的公共边之上那么，这个点该算作是哪个三角的呢

答案是只要你自己规定好就行，无所谓算哪个三角形的