扒一扒那些叫欧拉的定理们（七）——欧拉线定理的证明

早点关注我，精彩不迷路！

在前面的文章中，我们已经从空间几何欧拉定理介绍到了平面几何欧拉定理的拓展——九点圆定理，相关内容请戳：

扒一扒那些叫欧拉的定理们（六）——九点圆定理的证明

扒一扒那些叫欧拉的定理们（五）——平面几何欧拉定理的证明

扒一扒那些叫欧拉的定理们（四）——平面几何欧拉定理美学鉴赏

扒一扒那些叫欧拉的定理们（三）——简单多面体欧拉定理的抽象形式

扒一扒那些叫欧拉的定理们（二）——简单多面体欧拉定理的证明

扒一扒那些叫欧拉的定理们（一）——基本介绍和简单多面体欧拉定理

今天我们接着上一讲，来继续看平面几何欧拉定理的最后一部分内容：欧拉线定理，它也是在上一讲的九点圆定理的基础上的。

欧拉线定理内容

欧拉线定理

在平面几何中，欧拉线，或称尤拉线（图中的红线）是指过三角形的垂心（蓝）、外心（绿）、重心（黄）和九点圆圆心（红点）的一条直线。这四个点共线的结论，我们称为欧拉线定理。示意图如图所示：

图1 欧拉线定理图

（纯纯的几何之美。）

欧拉线定理分析和证明第一部分

共线（以及其对偶形式共点）的证明，是平面几何里一类非常典型，分量很重的形式，在接触梅涅劳斯定理（对偶形式赛瓦定理）以前，证明这个简直就是瞎蒙乱撞，没有个章法，这两个定理直接为这类证明提供了模板。但是，也有很多特殊情况，并不是走这个模式，需要根据条件灵活选用。比如这个欧拉线定理，众多角的相等，垂直关系使得其并不适合直接去套用梅涅劳斯定理，就像本身外心内心垂心的存在性证明也是用的很朴素的方法来说明的。因此，我们应该更多地直接从角180度，以及点的实际构造角度出发，比较直接地说明问题。

我们来看具体的证明过程：

图2 欧拉线定理证明第一部分图

如图，三角形ABC，HGO分别是其垂心，重心和外心，连接BO并延长，和外接圆O相交于D，连接AH，AD，CD和CH。

因为BD为外接圆O的直径，所以CD垂直BC，AD垂直AB；

又H为垂心，所以AH垂直BC，CH垂直AB；

因此CD//AH，HC//AD，ADCH为平行四边形，AH = DC；

又O，M分别为BD和BC中点，OM为三角形DBC的中位线，OM = DC / 2 = AH / 2；

连接AM，OM，OH，OH交AM于G'；显然，三角形AHG'相似于三角形MOG'，且对应边的比为AH / OM = 2，因此AG' = 2G'M，由于重心是中线靠近边的三等分点，因此重心G和G'重合，因此OGH三点共线。

点评：这其实就是一道比较传统，标准地各种利用相似，平行，以及平行四边形，三角形等最基本的几何性质来完成证明的题目，不是梅涅劳斯那类解法。这里证明三点共线的思路是，直接连接线段交在某点上，然后证明该点就是第三点。这个逻辑也是在梅涅劳斯定理以前最常用的方法，还有同一法也是类似的思路了，都属于构造法。而要到这个证明思路，一方面重心是中线的三等分点的性质很关键，有了这个起点，后续通过相似，中位线得到结论基本就顺水推舟了。

平面几何题目之妙处就在于，你永远不可能凭记忆去记住这些知识点，所有的应用也都是灵活的，想不想得到除了运气，大概率取决于你对其理解有多深，有多热爱，有怎样的经验，怎样剖析过它的本质。因为要证明一个结论，给你的条件是很多的，也并不是每一个都有用，怎么用的方向也需要判断，甚至达到终点还有多条路径，具体怎么走要靠大量经验积累而来的灵感。一道题的竞赛是有可能有偏差的，但是像围棋一样，水平是可以有明显的级别之分的。

用平面几何素材去考察一个人的智力，包括耐心，细致，逻辑思维，思维的宽广度，创造力等，实在是再好不过的素材了。

欧拉线定理分析和证明第二部分

接着我们来证明，九点圆圆心也在OGH所在的直线上，并且在GO的中点上。

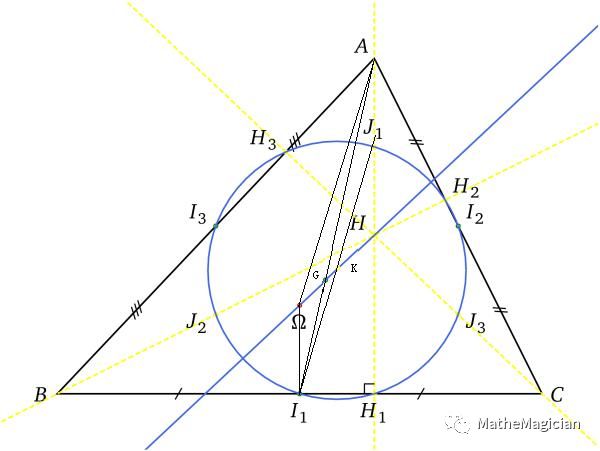
图3 欧拉线定理证明第二部分图

如图所示，H，G，Ω分别是图中的垂心，重心和外心。三角形三边中点为Ii，三高的垂足为Hi，顶点到垂心线段的中点为Ji，令HΩ和J1I1交于K。

显然，ΩI1为BC的中垂线，ΩI1垂直于BC，AH1也垂直BC，因此ΩI1//AH1，因此容易得到三角形GΩI1相似于三角形GHA；又由重心性质，AG = 2GI1，所以AH = 2ΩI1，因此，ΩI1 = J1H；

容易知道，三角形J1HK全等于三角形I1ΩK，于是，HK = KO；

同理，J2K = KI2，J3K = KI3，因此K为九点圆圆心，且K在OH连线的中点上，命题得证。

点评：我记得中学学平面几何那会，看到这么复杂的九点圆就怕，其实整体的宏伟，但是仍旧是由最基本的性质组成的，我们根据需要去逐步拆解挖掘就好，不能害怕复杂问题，要有顶层思维，拆解能力，才能在以后的工作生活中保持冷静的头脑，平面几何题目的训练就给了我这个机会，这么复杂的图都能攻克，其他的困难是不是只是换了个形式而已呢？

就本题的证明思路来看，和ΩGH三点共线的证明思路类似，还是把点通过相交找到，然后再证明就是我要的点，用到的也依然是相似，全等，中点，垂直，平行这些最基本的性质。但是把他们组合到一起，就能够形成一幅完整美丽的图形，形成一种整体美。就像泰姬陵，近处看一砖一瓦都是那么完美，而远处看起来整体的雄伟更是让人痴迷。魔术也是如此，每个动作都是基础的原理和手法，组合在一起就能脱胎于此变成一个真的魔术作品。

谨以此文纪念逝去的我曾为平面几何抛洒过热血的日子！

好了，平面几何的欧拉定理及相关的九点圆，欧拉线定理的内容到这里就全部介绍完毕了。

你以为欧拉定理就这么结束了了吗？欧拉就这么快没货了吗？

大错特错啦！接下来，我们进入复分析领域，看看在这个领域里，欧拉又给我们带来了怎样的惊喜！不要错过哦！

我们是谁：

MatheMagician，中文“数学魔术师”，原指用数学设计魔术的魔术师和数学家。既取其用数学来变魔术的本义，也取像魔术一样玩数学的意思。文章内容涵盖互联网，计算机，统计，算法，NLP等前沿的数学及应用领域；也包括魔术思想，流程鉴赏等魔术内容；以及结合二者的数学魔术分享，还有一些思辨性的谈天说地的随笔。希望你能和我一起，既能感性思考又保持理性思维，享受人生乐趣。欢迎扫码关注和在文末或公众号留言与我交流！

扫描二维码

关注更多精彩

扒一扒那些叫欧拉的定理们（六）——九点圆定理的证明

Si Stebbins Stack中的数学与魔术（十一）——《Woody on Stebbins》作品赏析

袁亚湘院士上《开讲啦》变数学魔术啦！

如果道具不能检查，那就毁了它！（二）——一般道具篇

利息浅谈（七）——万物皆投资

点击阅读原文，往期精彩不错过！