DAY2:有序数组的平方、长度最小的子数组和螺旋矩阵||(附带二维数组回形遍历)
有序数组的平方
977. 有序数组的平方 - 力扣(LeetCode)
暴力解:
class Solution {
public:
vector sortedSquares(vector& nums) {
for(int i=0;i 双指针
数组其实是有序的, 只不过负数平方之后可能成为最大数了。
那么数组平方的最大值就在数组的两端,不是最左边就是最右边,不可能是中间。
此时可以考虑双指针法了,i指向起始位置,j指向终止位置。
定义一个新数组result,和A数组一样的大小,让k指向result数组终止位置。
如果A[i] * A[i] < A[j] * A[j] 那么result[k--] = A[j] * A[j]; 。
如果A[i] * A[i] >= A[j] * A[j] 那么result[k--] = A[i] * A[i]; 。
如动画所示:(动画没法展示的话,可以看链接代码随想录 (programmercarl.com))
我在写这个代码遇到的困难是:
没有用一个新数组储存结果,直接在源代码上进行了修改,导致出现错误
class Solution {
public:
vector sortedSquares(vector& nums) {
int slow=0;
int fast=nums.size()-1;
int k=nums.size()-1;
vectornums1(nums.size(),0);
while(slow<=fast){
if(nums[slow]*nums[slow] 长度最小的子数组(leetcode:209)
老规矩,还是先暴力解
209. 长度最小的子数组 - 力扣(LeetCode)
暴力解:
思路很简单,两个for循环,复杂度为O(n)
注意:暴力解会超时的
class Solution {
public:
int minSubArrayLen(int target, vector& nums) {
int result=INT_MAX;
for(int i=0;i=target){
result=min(k,result);
break;
}
}
}
if(result==INT_MAX)return 0;
return result;
}
}; 滑动窗口
卡哥解释的这个较为详细
接下来就开始介绍数组操作中另一个重要的方法:滑动窗口。
所谓滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。
在暴力解法中,是一个for循环滑动窗口的起始位置,一个for循环为滑动窗口的终止位置,用两个for循环 完成了一个不断搜索区间的过程。
那么滑动窗口如何用一个for循环来完成这个操作呢。
首先要思考 如果用一个for循环,那么应该表示 滑动窗口的起始位置,还是终止位置。
如果只用一个for循环来表示 滑动窗口的起始位置,那么如何遍历剩下的终止位置?
此时难免再次陷入 暴力解法的怪圈。
所以 只用一个for循环,那么这个循环的索引,一定是表示 滑动窗口的终止位置。
那么问题来了, 滑动窗口的起始位置如何移动呢?
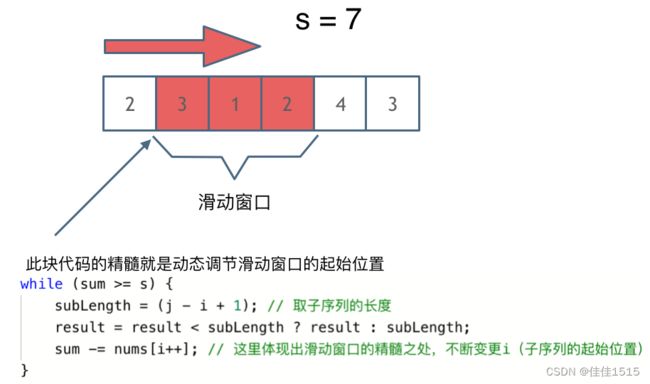
这里还是以题目中的示例来举例,s=7, 数组是 2,3,1,2,4,3,来看一下查找的过程:
最后找到 4,3 是最短距离。
其实从动画中可以发现滑动窗口也可以理解为双指针法的一种!只不过这种解法更像是一个窗口的移动,所以叫做滑动窗口更适合一些。
在本题中实现滑动窗口,主要确定如下三点:
- 窗口内是什么?
- 如何移动窗口的起始位置?
- 如何移动窗口的结束位置?
窗口就是 满足其和 ≥ s 的长度最小的 连续 子数组。
窗口的起始位置如何移动:如果当前窗口的值大于s了,窗口就要向前移动了(也就是该缩小了)。
窗口的结束位置如何移动:窗口的结束位置就是遍历数组的指针,也就是for循环里的索引。
解题的关键在于 窗口的起始位置如何移动,如图所示:
可以发现滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。
本人理解的话,就是双指针做法嘛,其实个人感觉暴力解也算一种不够先进的双指针,
这个滑动窗口移动结束位置属实是第一次见,通过一种独特的方式更新起始位置,将复杂度降到O(n),感觉很棒
class Solution {
public:
int minSubArrayLen(int target, vector& nums) {
int fast=0;
int slow=0;
int sum=0;
int result=INT_MAX;
for(fast=0;fast=target){
result=min(result,fast-slow+1);
sum-=nums[slow];
slow++;
}//注意这个是while,因为可能slow++一次后还大于等于target
}
if(result==INT_MAX)return 0;
else{return result;}
}
}; 螺旋矩阵II
59. 螺旋矩阵 II - 力扣(LeetCode)
本人第一印象是一个二维数组回形遍历的变形,也就是一个顺时针的遍历吧,而且比普通回形遍历简单一些,因为是个正方形嘛,在这里就直接给出代码了哈
class Solution {
public:
vector> generateMatrix(int n) {
vector>result(n,vector(n,0));
if(n==1){result[0][0]=1;
return result;
}
int cnt=1;
int i=0,j=0;
while(cnt<=n*n){
result[i][j]=cnt;
cnt++;
while(j+1=0&&result[i][j-1]==0){
result[i][--j]=cnt;
cnt++;
}
while(i-1>=0&&result[i-1][j]==0){
result[--i][j]=cnt;
cnt++;
}
j++;
}
return result;
}
}; 普通二维回形遍历
忘了连接北大了,这个好像打不开题目链接,我就在ppt上找一下
给你们看一下这两个思路
注意这个层数的计算方法是行数和列数中的较小值除以2向上取整
这个实现的代码为:
#include
#include
using namespace std;
int main() {
int row, col;
cin >> row >> col;
vector>nums(row, vector(col,0));
for (int i = 0;i < row;i++) {
for (int j = 0;j < col;j++) {
cin >> nums[i][j];
}
}
int n = row > col ? (col + 1) / 2 : (row + 1) / 2;
for (int a = 0;a < n;a++) {
int startrow = a, endrow = row - a - 1;
int startcol = a, endcol = col - a - 1;
if (startrow == endrow) {
for (int i = startcol;i <= endcol;i++) {
cout << nums[startrow][i]< startcol;i--) {
cout << nums[endrow][i] << endl;
}
for (int i = endrow;i > startrow;i--) {
cout << nums[i][startcol] << endl;
}
}
}
} 螺旋矩阵||就是采用一种贪吃蛇的做法
下面给出一种更普遍的代码(回形遍历的代码)
#include
#include
using namespace std;
int dx[4] = {0,1,0,-1};
int dy[4] = { 1,0,-1,0 };
int main() {
int row, col;
cin >> row >> col;
vector>nums(row, vector(col,-1));
for (int i = 0;i < row;i++) {
for (int j = 0;j < col;j++) {
cin >> nums[i][j];
}
}
int cnt = 1;
int x = 0, y = 0;
int d = 0;
cout << nums[x][y] << endl;
while (cnt < row * col) {
while (true) {
nums[x][y] = -1;
int tx = x + dx[d];
int ty = y + dy[d];
if (tx < 0 || tx >= row || ty<0 || ty>=col || nums[tx][ty] == -1)break;
cnt++;
cout << nums[tx][ty] << endl;
x = tx, y = ty;
if (cnt == row * col)break;
}
d = (d + 1) % 4;
}
}