华为机考108题(c++)(52-61)
HJ52 计算字符串的编辑距离
描述
Levenshtein 距离,又称编辑距离,指的是两个字符串之间,由一个转换成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符,插入一个字符,删除一个字符。编辑距离的算法是首先由俄国科学家 Levenshtein 提出的,故又叫 Levenshtein Distance 。
例如:
字符串A: abcdefg
字符串B: abcdef
通过增加或是删掉字符 ”g” 的方式达到目的。这两种方案都需要一次操作。把这个操作所需要的次数定义为两个字符串的距离。
要求:
给定任意两个字符串,写出一个算法计算它们的编辑距离。
数据范围:给定的字符串长度满足 1≤len(str)≤1000
输入描述:
每组用例一共2行,为输入的两个字符串
输出描述:
每组用例输出一行,代表字符串的距离
方法一:动态规划
#include
#include
#include
#include
using namespace std;
int main() {
string str1, str2;
while (cin >> str1 >> str2) {
vector> dp(str1.size() + 1, vector(str2.size() + 1, 0));
for (int i = 1; i <= str2.size(); i++) dp[0][i] = i;//str1从0个字符变成str2的i个字符需要i个插入操作
for (int i = 1; i <= str1.size(); i++) dp[i][0] = i;//str1从i个字符变成str2的0个字符也需要i个删除操作
for(int i=1;i<=str1.size();i++){
for (int j = 1; j <= str2.size(); j++) {
int op1 = dp[i-1][j] + 1;//删除字符str1[i-1]
int op2 = dp[i][j-1] + 1;//删除字符str2[j-1]
int op3 = dp[i-1][j-1];//替换操作
if(str1[i-1] != str2[j-1]){
op3++;
}
dp[i][j] = min(min(op1, op2), op3);//替换操作和删除操作取最小
}
}
cout << dp[str1.size()][str2.size()] << endl;
}
}
方法二:滚动数组+动态规划
#include
#include
#include
#include
using namespace std;
int main() {
string str1, str2;
while (cin >> str1 >> str2) {
vector dp(str2.size() + 1, 0);
for(int i = 0; i <= str2.size(); i++)//初始化第一行
dp[i] = i;
for(int i = 1; i <= str1.size(); i++){
dp[0] = i;//初始化dp[0],i->0需要i个删除操作
int l = dp[0] - 1;
for (int j = 1; j <= str2.size(); j++) {
int curr = dp[j];//保留当前的值,作为dp[j+1]的左上角值
dp[j] = min(min(dp[j] + 1, dp[j-1] + 1), ((str1[i-1] == str2[j-1])?0:1) + l);
l = curr;//更新左上角值
}
}
cout << dp[str2.size()]<< endl;
}
}
HJ53 杨辉三角的变形
描述
以上三角形的数阵,第一行只有一个数1,以下每行的每个数,是恰好是它上面的数、左上角数和右上角的数,3个数之和(如果不存在某个数,认为该数就是0)。
求第n行第一个偶数出现的位置。如果没有偶数,则输出-1。例如输入3,则输出2,输入4则输出3,输入2则输出-1。
数据范围: 1≤n≤109
输入描述:
输入一个int整数
输出描述:
输出返回的int值
方法一:数组模拟(超出空间)
#include
#include
using namespace std;
int main(){
int n;
while(cin >> n){
vector > matrix(n, vector(2 * n - 1, 0)); //一共n行,最下面一行最多有2*n-1个元素
matrix[0][n - 1] = 1; //顶角
matrix[n - 1][0] = matrix[n - 1][2 * n - 2] = 1; //两个底角
for(int i = 1; i < n; i++)
for(int j = 1; j < 2 * n - 2; j++)
matrix[i][j] = matrix[i - 1][j - 1] + matrix[i - 1][j] + matrix[i - 1][j + 1];
for(int i = 0; i < 2 * n - 1; i++){
if(matrix[n - 1][i] != 0 && matrix[n - 1][i] % 2 == 0){ //非0偶数
cout << i + 1 << endl; //输出下标加1;
break;
}
if(i >= n - 1 && matrix[n - 1][i] == 1){ //过一半还没有找到偶数且遇到了1代表永远找不到了
cout << -1 << endl;
break;
}
}
}
return 0;
}
方法二:数学规律
#include
using namespace std;
int main(){
int n;
while(cin >> n){
if(n <= 2) //小于等于2的行没有偶数
cout << -1 << endl;
else{
if(n % 2) //奇数行偶数在第2个
cout << 2 << endl;
else if(n % 4 == 2) //偶数除4余2的在第4个
cout << 4 << endl;
else if(n % 4 == 0) //整除4的在第3个
cout << 3 << endl;
}
}
return 0;
}
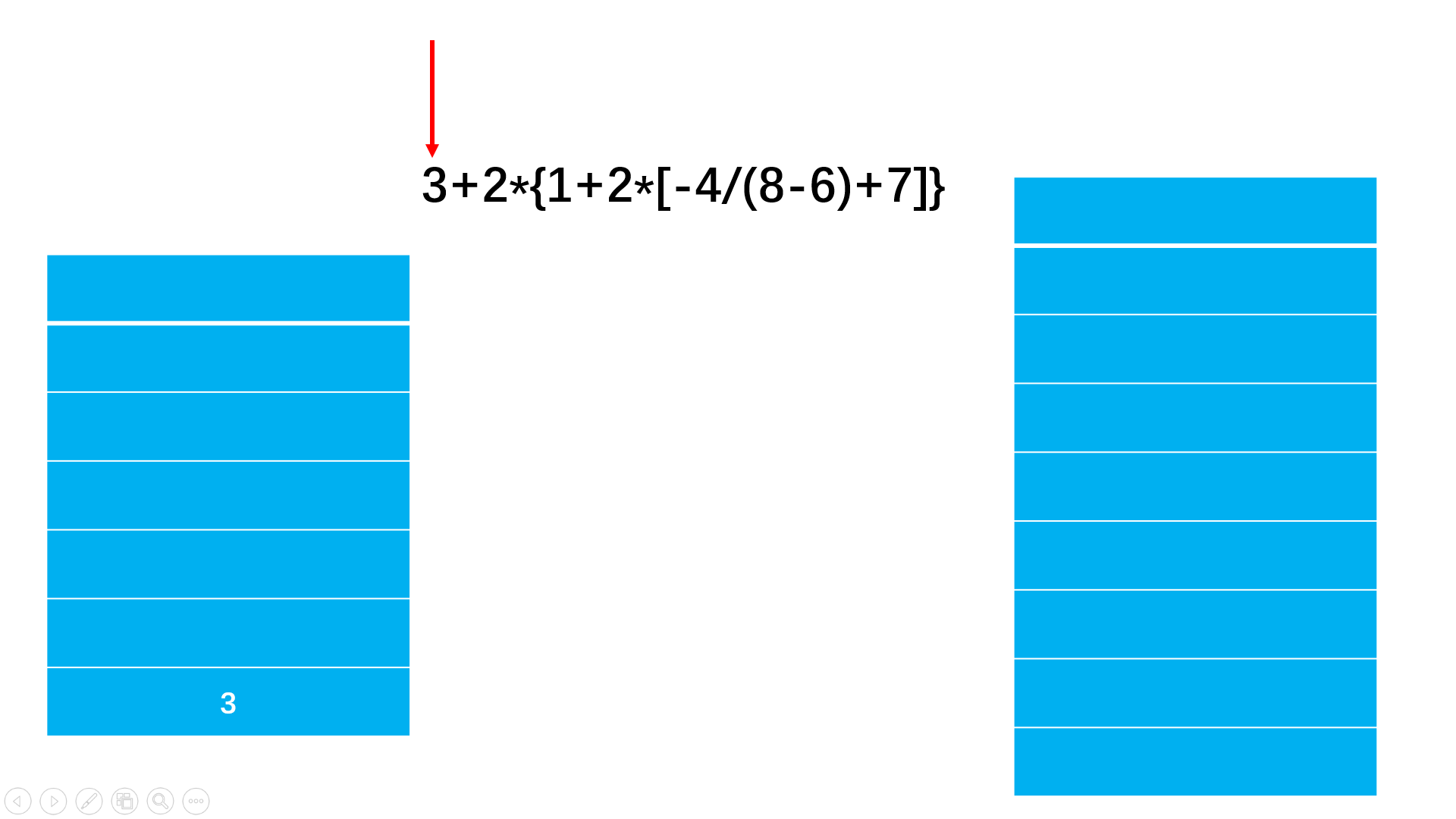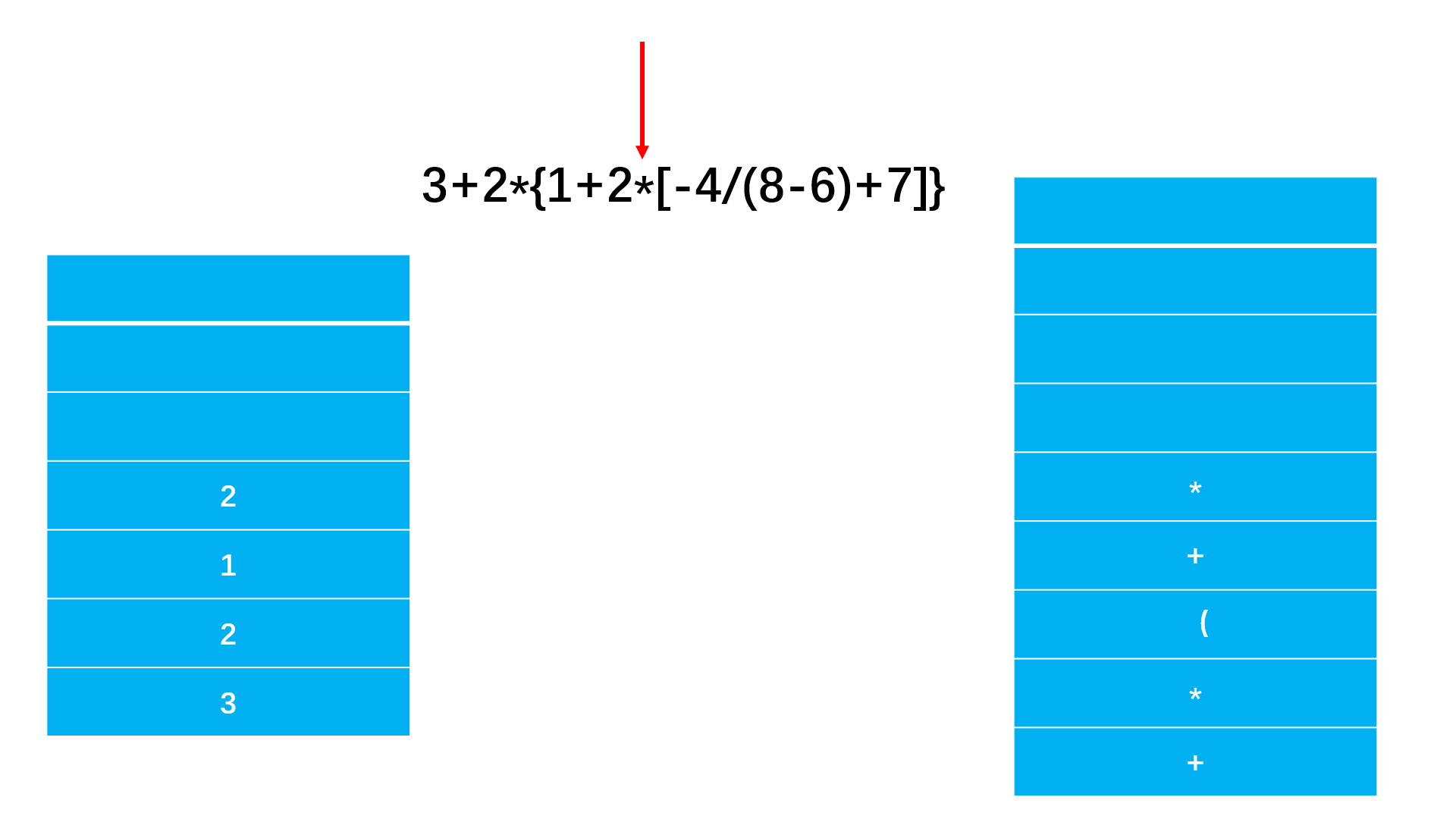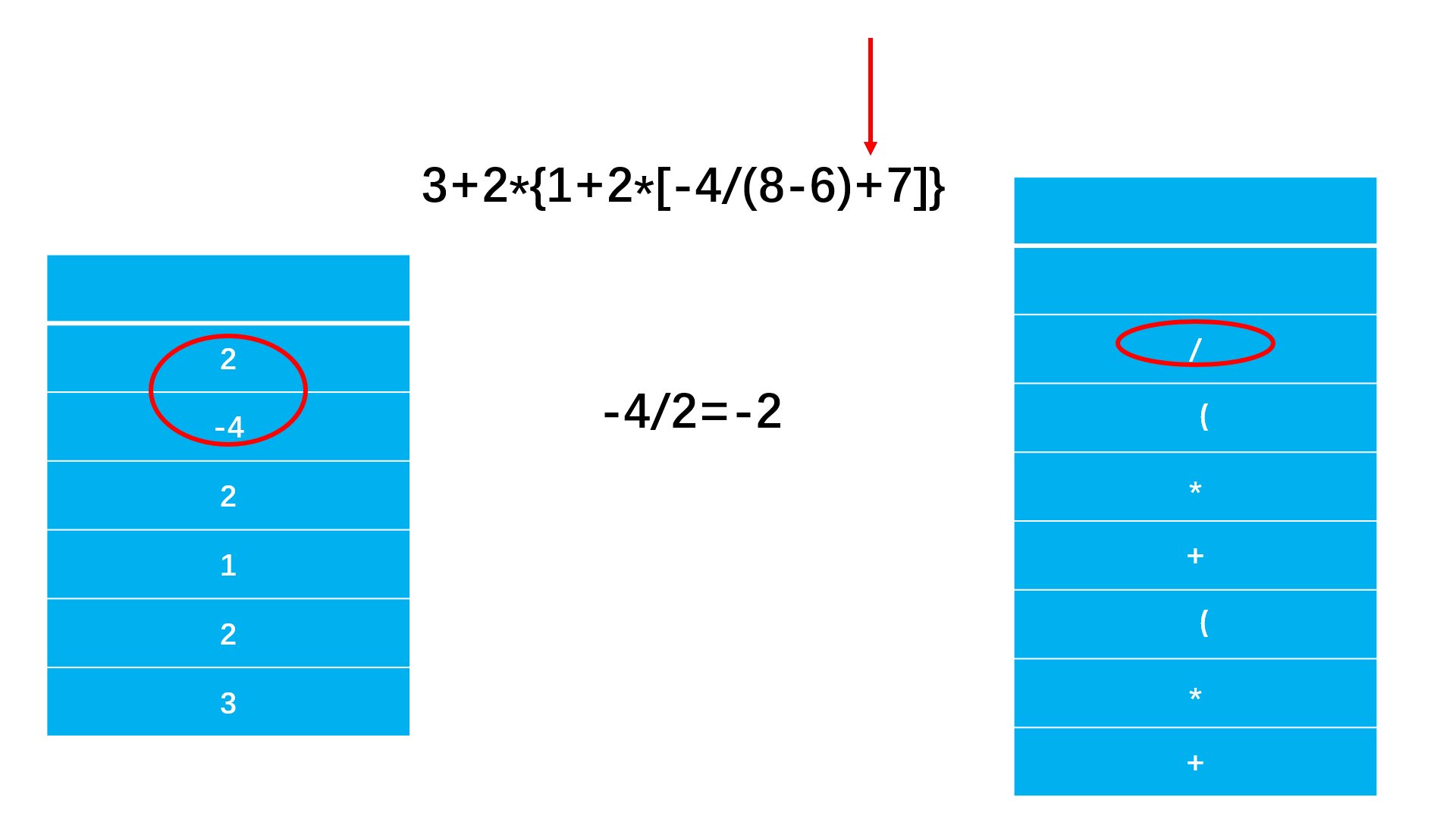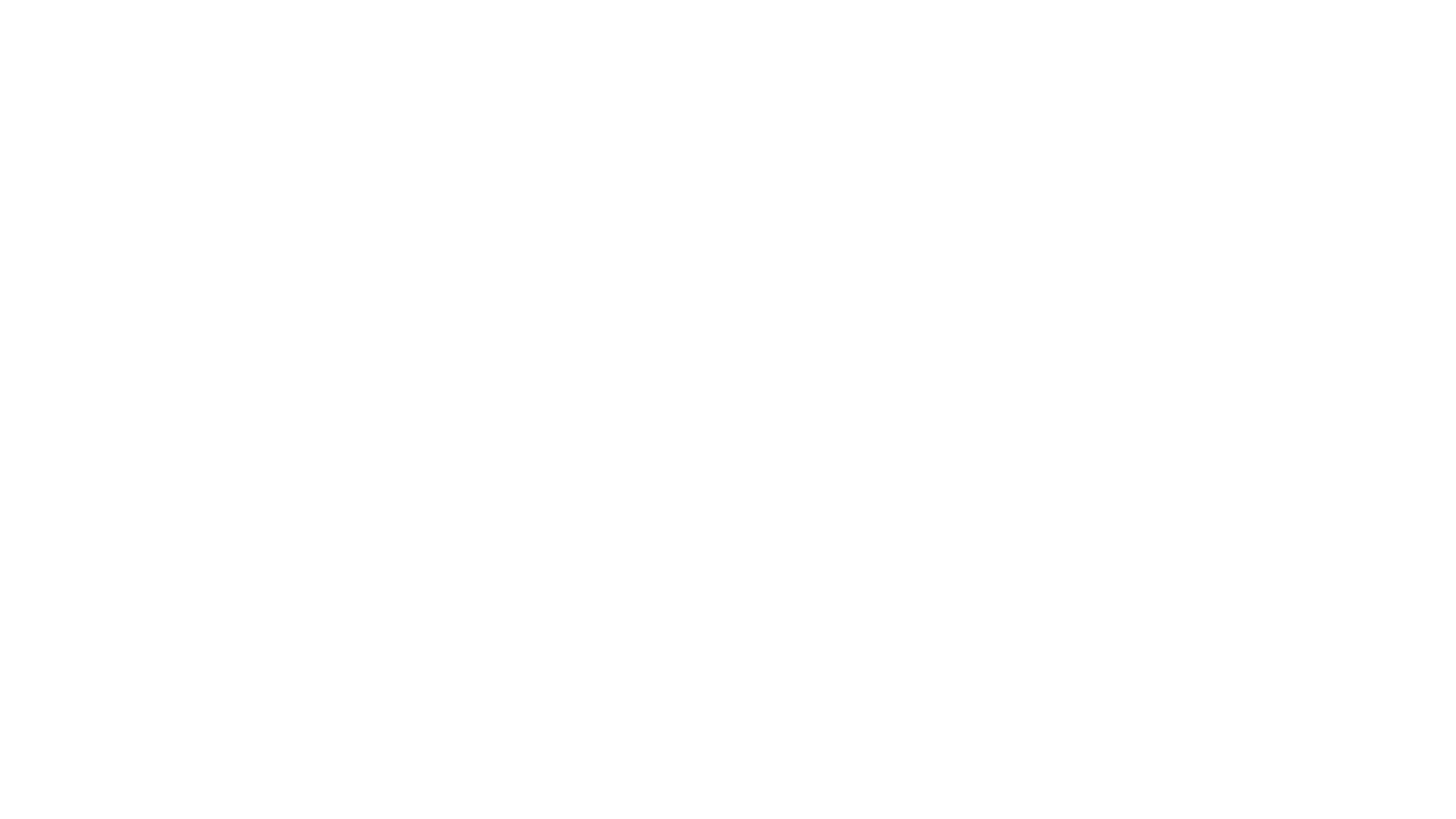
HJ54 表达式求值
描述
给定一个字符串描述的算术表达式,计算出结果值。
输入字符串长度不超过 100 ,合法的字符包括 ”+, -, *, /, (, )” , ”0-9” 。
数据范围:运算过程中和最终结果均满足∣val∣≤2^31−1 ,即只进行整型运算,确保输入的表达式合法
输入描述:
输入算术表达式
输出描述:
计算出结果值
方法一:递归
#include
#include
#include
using namespace std;
int compute(string& s, int left, int right){
char op = '+'; //默认加开始
int num = 0;
vector st;
for(int i = left; i <= right; i++){
if(isdigit(s[i])) //数字
num = num * 10 + s[i] - '0'; //计算该部分数字总和
if(s[i] == '('){ //进入左括号
int layer = 0; //统计左括号层数
int j = i;
while(j <= right){ //遍历到右边
if(s[j] == '(')
layer++; //遇到左括号,层数累加
else if(s[j] == ')'){
layer--; //遇到右括号层数递减
if(layer == 0) //直到层数为0
break;
}
j++;
}
num = compute(s, i + 1, j - 1); //递归计算括号中的部分
i = j + 1;
}
if(!isdigit(s[i]) || i == right){ //遇到运算符或者结尾
switch(op){ //根据运算符开始计算
case '+': st.push_back(num); break; //加减法加入到末尾
case '-': st.push_back(-num); break;
case '*': st.back() *= num; break; //乘除法与末尾计算
case '/': st.back() /= num; break;
}
op = s[i]; //修改为下一次的运算符
num = 0;
}
}
int res = 0;
for(int x : st) //累加和
res += x;
return res;
}
int main(){
string s;
while(cin >> s){
cout << compute(s, 0, s.length() - 1) << endl;
}
return 0;
}
方法二:双栈法
#include
#include
using namespace std;
void compute(stack& st1, stack& st2){ //根据栈顶运算符弹出栈顶两个元素进行运算
int b = st1.top();
st1.pop();
int a = st1.top();
st1.pop();
char op = st2.top(); //栈顶运算符
st2.pop();
if(op == '+') a = a + b; //加
else if(op == '-') a = a - b; //减
else if(op == '*') a = a * b; //乘
else if(op == '/') a = a / b; //除
st1.push(a);
}
bool priority(char m, char n){ //比较运算符优先级
if(m == '(') //括号优先级最高
return false;
else if((m == '+' || m == '-') && (n == '*' || n == '/')) //加减法小于乘除法
return false;
return true;
}
int main(){
string s;
while(cin >> s){
stack st1; //记录运算数字
stack st2; //记录运算符
st2.push('('); //整个运算式添加括号
s += ')';
bool flag = false;
for(int i = 0; i < s.length(); i++){
if(s[i] == '(') //如果是左括号都在运算符栈加入(
st2.push('(');
else if(s[i] == ')'){ //遇到右括号
while(st2.top() != '('){ //弹出开始计算直到遇到左括号
compute(st1, st2);
}
st2.pop(); //弹出左括号
} else if(flag){ //运算符
while(priority(st2.top(), s[i])){ //比较运算优先级
compute(st1, st2); //可以直接计算
}
st2.push(s[i]); //需要将现阶段加入栈中等待运算
flag = false;
} else{ //数字
int j = i; //记录起始
if(s[j] == '-' || s[j] == '+') //正负号
i++;
while(isdigit(s[i])){
i++;
}
string temp = s.substr(j, i - j);
st1.push(stoi(temp)); //截取数字部分,转数字
i--;
flag = true; //数字结束,下一次flag为true就是运算符了
}
}
cout << st1.top() << endl; //输出
}
return 0;
}
HJ55 挑7
描述
输出 1到n之间 的与 7 有关数字的个数。
一个数与7有关是指这个数是 7 的倍数,或者是包含 7 的数字(如 17 ,27 ,37 ... 70 ,71 ,72 ,73...)
数据范围:1≤n≤30000
输入描述:
一个正整数 n 。( n 不大于 30000 )
输出描述:
一个整数,表示1到n之间的与7有关的数字个数。
方法一:连除法判断
#include
using namespace std;
bool select7(int i){
if(i % 7 == 0) //7的倍数
return true;
while(i != 0){ //连除法
if(i % 10 == 7) //数字里包含7
return true;
i /= 10;
}
return false;
}
int main(){
int n;
while(cin >> n){
int count = 0;
for(int i = 1; i <= n; i++) //穷举1到n
if(select7(i)) //查看是否符合要求
count++;
cout << count << endl;
}
return 0;
}
#include
#include
using namespace std;
int main(){
int n;
while(cin >> n){
int count = 0;
for(int i = 7; i <= n; i++) //枚举7到n
if(i % 7 == 0 || to_string(i).find('7', 0) != string::npos) //整除7或者转化字符串后能找到字符7
count++;
cout << count << endl;
}
return 0;
}
HJ56 完全数计算
描述
完全数(Perfect number),又称完美数或完备数,是一些特殊的自然数。
它所有的真因子(即除了自身以外的约数)的和(即因子函数),恰好等于它本身。
例如:28,它有约数1、2、4、7、14、28,除去它本身28外,其余5个数相加,1+2+4+7+14=28。
输入n,请输出n以内(含n)完全数的个数。
数据范围:1≤n≤5×105
输入描述:
输入一个数字n
输出描述:
输出不超过n的完全数的个数
方法一:
大数学家欧拉曾推算出完全数的获得公式:如果p是质数,且2^p-1也是质数,那么(2^p-1)X2^(p-1)便是一个完全数。
例如p=2,是一个质数,2^p-1=3也是质数,(2^p-1)X2^(p-1)=3X2=6,是完全数。
例如p=3,是一个质数,2^p-1=7也是质数,(2^p-1)X2^(p-1)=7X4=28,是完全数。
例如p=5,是一个质数,2^p-1=31也是质数,(2^p-1)X2^(p-1)=31X16=496是完全数。
当2^p-1是质数的时候,称其为梅森素数。到2013年2月6日为止,人类只发现了48个梅森素数,较小的有3、7、31、127等
//C++
#include
#include
using namespace std;
bool is_prime(int p);
// 如果p是质数,且2^p-1也是质数,那么(2^p-1)X2^(p-1)便是一个完全数
int main()
{
int n;
while(cin >> n)
{
int count = 0;
for(int p=2; p0 && perfect_num 方法二:
#include
using namespace std;
int main()
{
int n; //待输入的数
while(cin>>n){
int count=0; //计数器
//遍历从2到n的每一个数,并在下一层for计算是否为完全数
for(int k=2;k<=n;k++)
{
int sum=1; //每个数都包含1这个因数
for(int i=2;i<=k/2;i++) //除以2:根据题干推出的缩小i范围的方法
{
if(k%i==0)
sum=sum+i;
}
if(k==sum)
count++;
}
cout< HJ57 高精度整数加法
描述
输入两个用字符串 str 表示的整数,求它们所表示的数之和。
数据范围: 1≤len(str)≤10000
输入描述:
输入两个字符串。保证字符串只含有'0'~'9'字符
输出描述:
输出求和后的结果
方法一:
#include
#include
#include
#include
using namespace std;
// 将两个字符串扔到两个栈中,逐个斩当头,直到两个栈都空
// 主要是注意进位问题,最后一位的问题
int main() {
string s1, s2;
while (cin >> s1 >> s2) {
string ans;
stack st1;
stack st2;
for (char c : s1) {
st1.push(c);
}
for (char c : s2) {
st2.push(c);
}
int flag = 0;
while (st1.size() != 0 || st2.size() != 0) {
int temp = 0;
if (st1.size() != 0) {
temp += st1.top() - '0';
st1.pop();
}
if (st2.size() != 0) {
temp += st2.top() - '0';
st2.pop();
}
// temp和flag加完后再取余和除以,这是考虑到加完flag后刚好为10的情况
ans += (temp + flag) % 10 + '0';
flag = (temp + flag) / 10;
// 对于两个栈都空之前,判断有没有进位,如果进位则直接加'1'
if (flag == 1 && st1.size() == 0 && st2.size() ==0)
ans += '1';
}
// 记得反转一下再输出
reverse(ans.begin(), ans.end());
cout << ans << endl;
}
return 0;
}
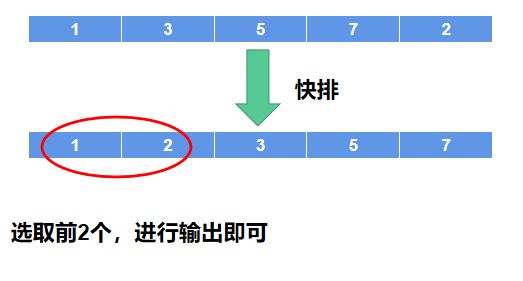
HJ58 输入n个整数,输出其中最小的k个
描述
输入n个整数,找出其中最小的k个整数并按升序输出
本题有多组输入样例
数据范围:1≤n≤1000 ,输入的整数满足 1≤val≤10000
输入描述:
第一行输入两个整数n和k
第二行输入一个整数数组
输出描述:
从小到大输出最小的k个整数,用空格分开
方法一:暴力方法
#include
using namespace std;
int main()
{
int n,k;
while(cin>>n>>k)
{ //输入n和k
vector num;
for(int i=0;i>temp;
num.push_back(temp);
}
sort(num.begin(),num.end());//对n个数进行升序排序
for(int i=0;i 方法二:堆方法
#include
using namespace std;
int main()
{
int n = 0, k = 0;
while(cin >> n >> k)
{
vector vec;
int num = 0;
while(n--)
{
cin >> num;
vec.push_back(num);
}
//建堆k*logk
vector heap(vec.begin(), vec.begin() + k);
make_heap(heap.begin(), heap.end(), less());
//插入(n - k)*logk
for(int i = k; i < vec.size(); i++)
{
if(vec[i] < heap[0])
{
//插入一个更小的
heap.push_back(vec[i]);
push_heap(heap.begin(), heap.end());
//弹出一个最大的
pop_heap(heap.begin(), heap.end());
heap.pop_back();
}
}
//从小到大输出,k*logk + k
sort(heap.begin(), heap.end());
for(int i = 0; i < heap.size(); i++)
{
cout << heap[i];
if(i != heap.size() - 1)
{
cout << " ";
}
}
cout << endl;
}
}
HJ59 找出字符串中第一个只出现一次的字符
描述
找出字符串中第一个只出现一次的字符
数据范围:输入的字符串长度满足1≤n≤1000
输入描述:
输入一个非空字符串
输出描述:
输出第一个只出现一次的字符,如果不存在输出-1
方法一:哈希表统计频率
#include
#include
#include
using namespace std;
int firstNotRepeat(string& str) {
unordered_map mp;
for(int i = 0; i < str.length(); i++) //统计每个字符出现的次数
mp[str[i]]++;
for(int i = 0; i < str.length(); i++) //找到第一个只出现一次的字母
if(mp[str[i]] == 1)
return i;
return -1; //没有找到
}
int main(){
string s;
while(getline(cin, s)){
int pos = firstNotRepeat(s); //找到该该字符的位置
if(pos == -1) //没找到输出-1
cout << -1 << endl;
else
cout << s[pos] << endl; //输出字符
}
return 0;
}
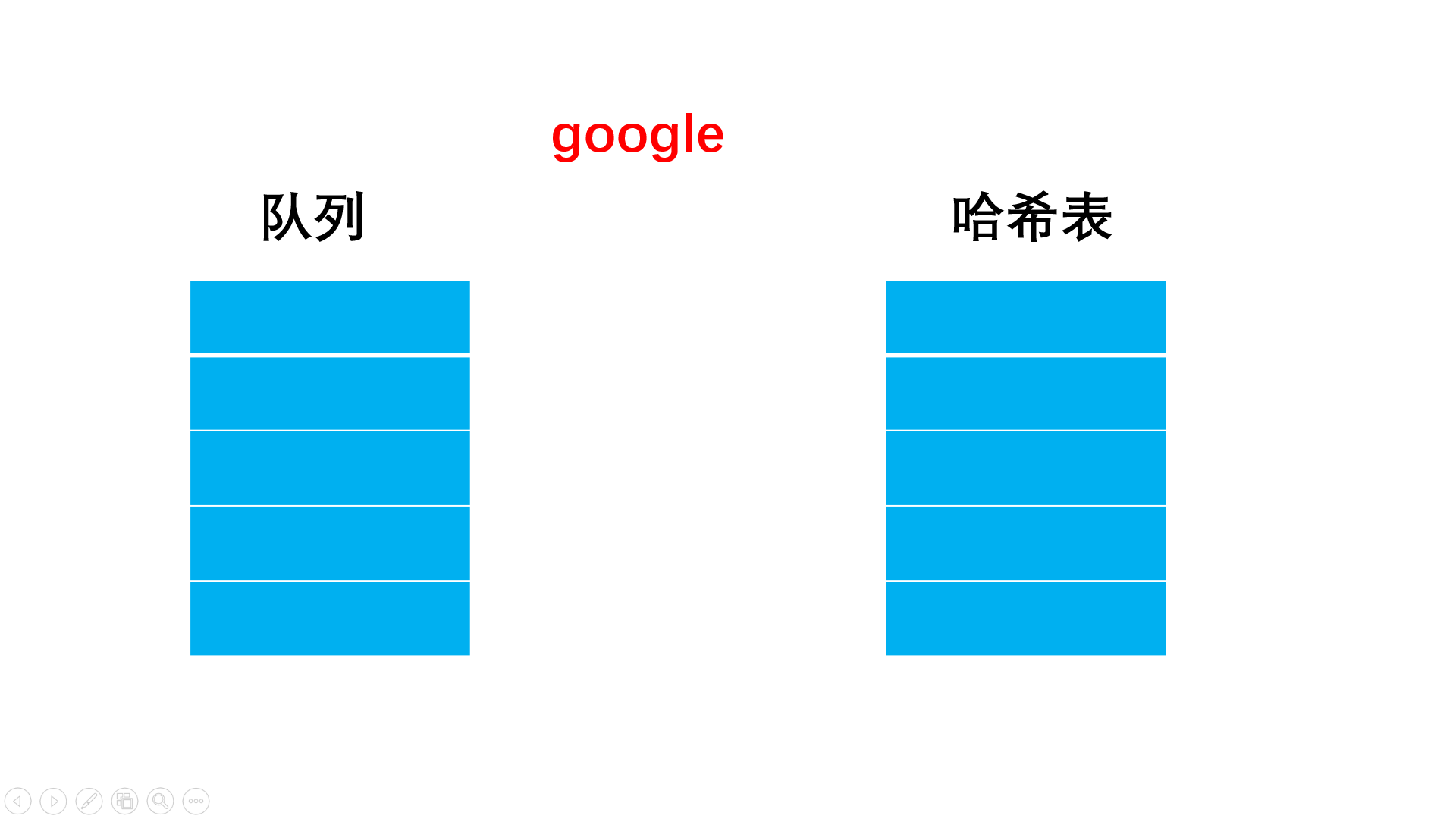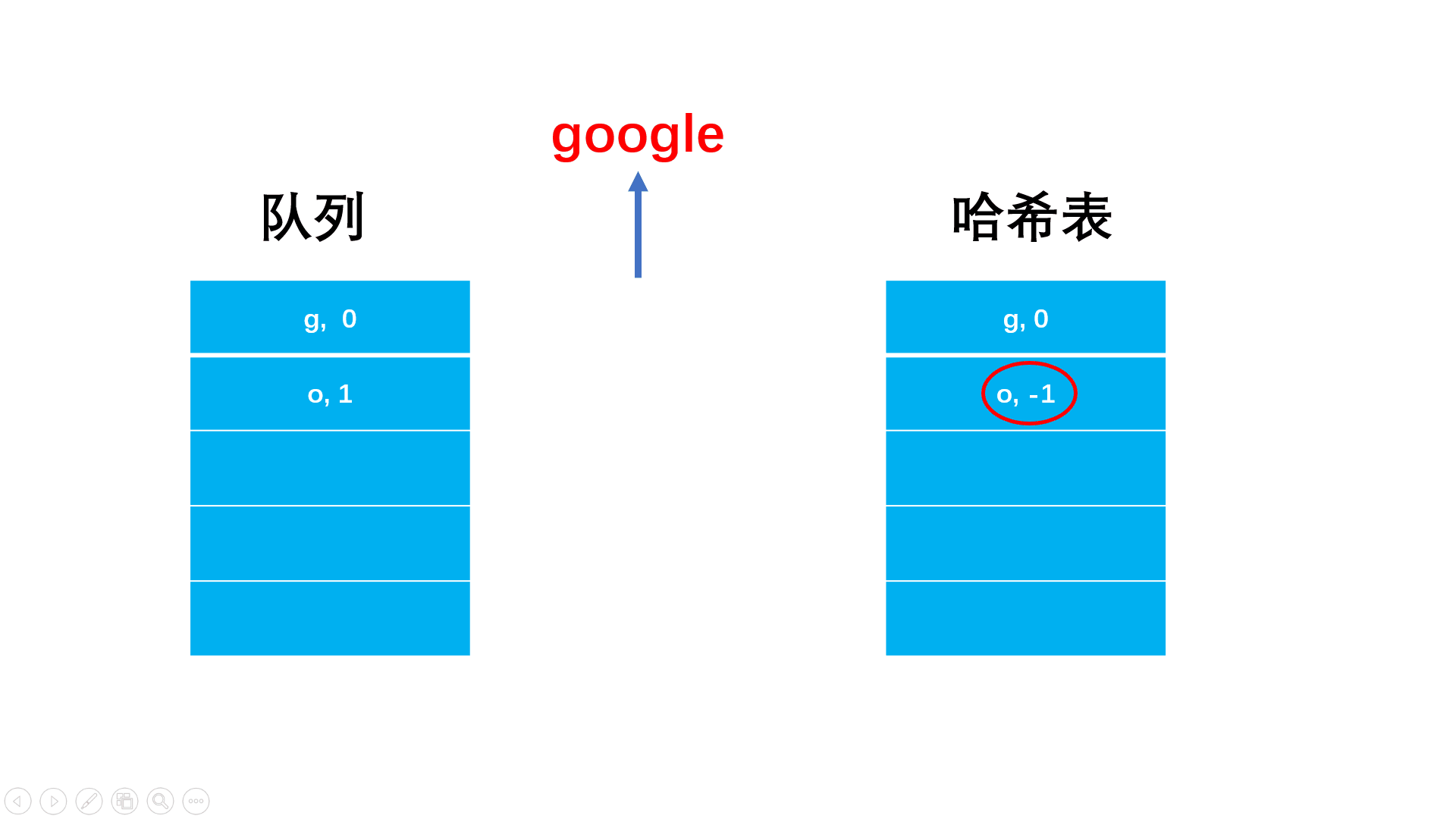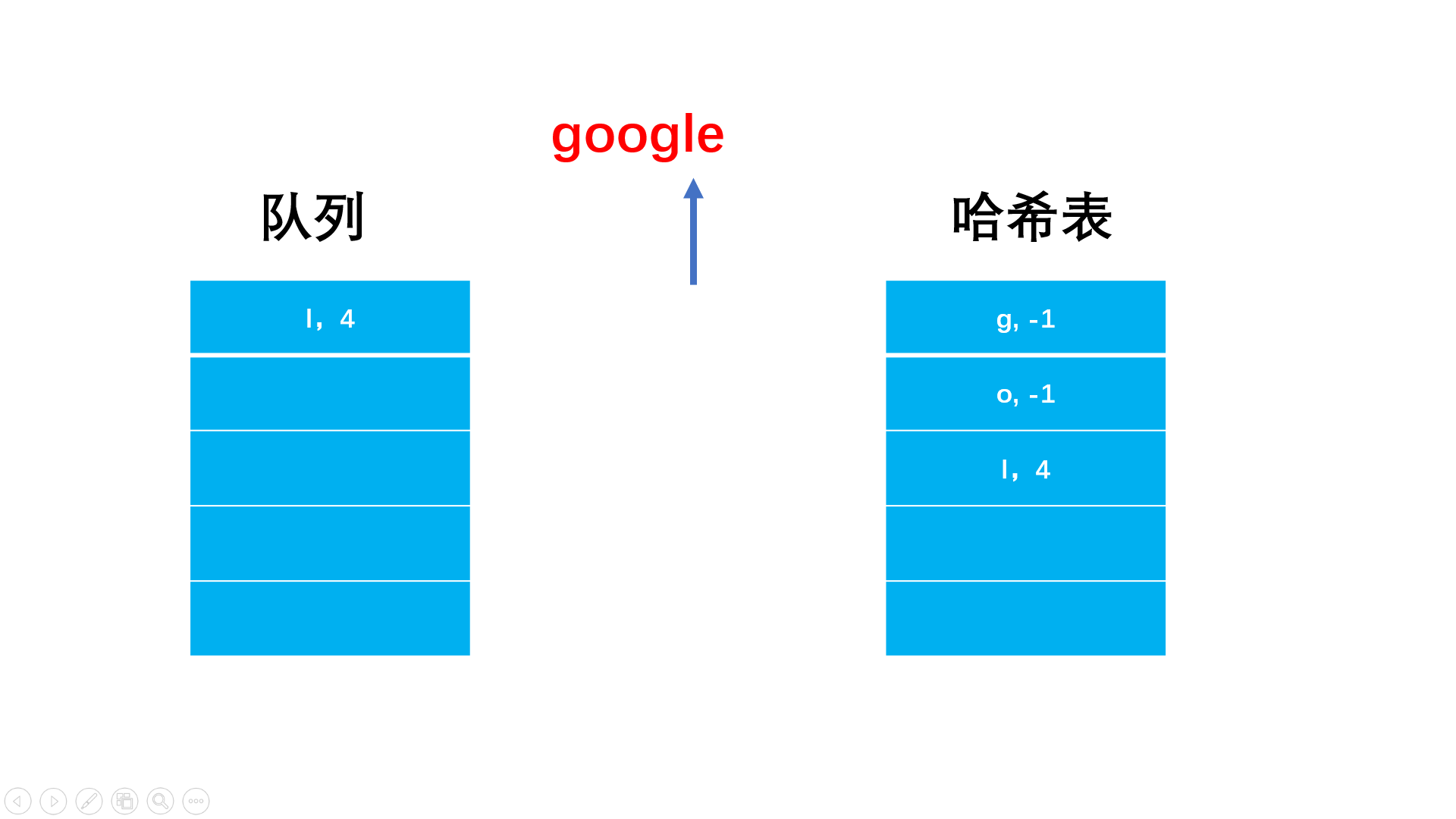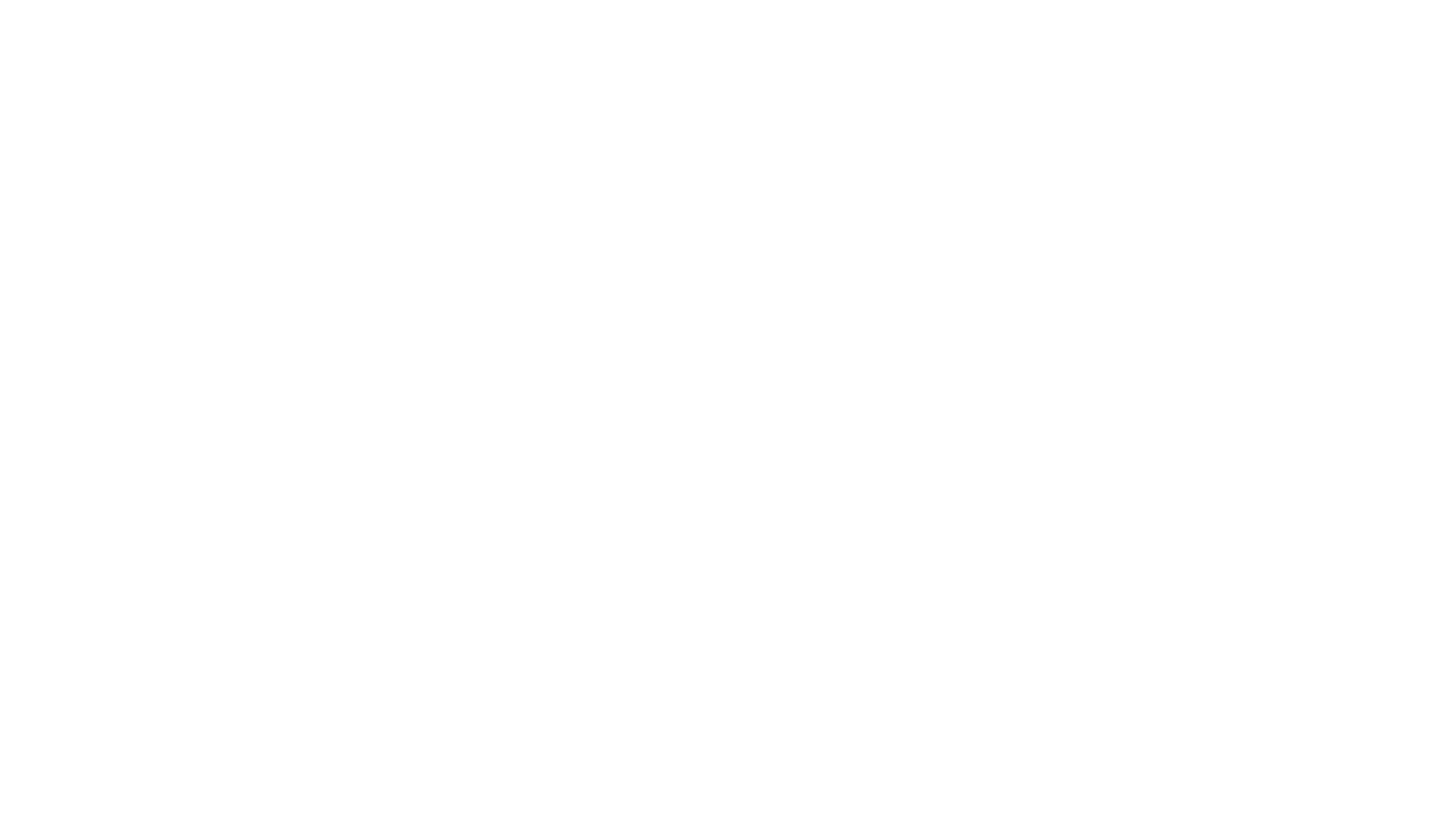
方法二:队列+哈希表统计位置
#include
#include
#include
#include
using namespace std;
int firstNotRepeat(string& str) {
unordered_map mp; //统计字符出现的位置
queue > q;
for(int i = 0; i < str.length(); i++){
if(!mp.count(str[i])){ //没有出现过的字符
mp[str[i]] = i;
q.push(make_pair(str[i], i));
}else{ //找到重复的字符
mp[str[i]] = -1; //位置置为-1
while(!q.empty() && mp[q.front().first] == -1) //弹出前面所有的重复过的字符
q.pop();
}
}
return q.empty() ? -1 : q.front().second;
}
int main(){
string s;
while(getline(cin, s)){
int pos = firstNotRepeat(s); //找到该该字符的位置
if(pos == -1) //没找到输出-1
cout << -1 << endl;
else
cout << s[pos] << endl; //输出字符
}
return 0;
}
方法三:首次末次比较解法
#include
using namespace std;
int main()
{
string str;
while(cin >> str)
{
bool flag = false;//flag用来判断是否存在只出现一次的字符
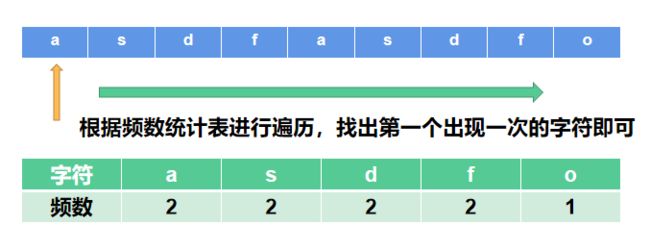
for(int i =0;i 方法四:频数统计方法
#include
using namespace std;
int main()
{
string str;
while(cin>>str)
{
int count[26] = {0};
for(int i = 0; i < str.size(); i++)//统计每个字符出现的频数
{
count[str[i] - 'a']++;
}
bool flag = false;//用户判断是否存在只出现一次的字符
for(int i = 0; i < str.size(); i++)
{
if (count[str[i] - 'a'] == 1)//判断当前字符是否只出现一次
{
cout< HJ60 查找组成一个偶数最接近的两个素数
描述
任意一个偶数(大于2)都可以由2个素数组成,组成偶数的2个素数有很多种情况,本题目要求输出组成指定偶数的两个素数差值最小的素数对。
数据范围:输入的数据满足 4≤n≤1000
输入描述:
输入一个大于2的偶数
输出描述:
从小到大输出两个素数
方法一:穷举
#include
using namespace std;
bool isPrime(int n){ //判断数字n是否是素数
for(int i = 2; i < n; i++){ //遍历到n-1
if(n % i == 0) //如果由因子就不是素数
return false;
}
return true; //遍历完都没有就是素数
}
int main(){
int n;
while(cin >> n){
int mindis = n;
pair res; //记录两个素数
for(int i = 2; i < n; i++){ //遍历2到n找到两个素数
if(isPrime(i) && isPrime(n - i)){ //两个数都是素数的时候
if(abs(n - i - i) < mindis){ //找距离最小
res = {i, n - i}; //更新最小
mindis = abs(n - i - i);
}
}
}
cout << res.first << endl << res.second << endl;
}
return 0;
}
方法二:穷举优化
#include
#include
using namespace std;
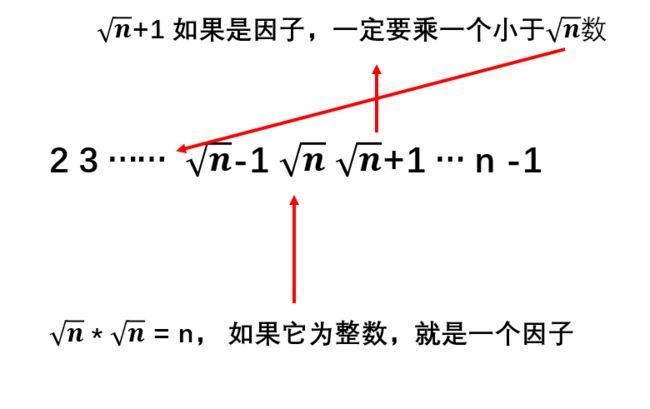
bool isPrime(int n){ //判断数字n是否是素数
for(int i = 2; i * i <= n; i++){ //遍历到根号n
if(n % i == 0)
return false;
}
return true;
}
int main(){
int n;
while(cin >> n){
int mindis = n;
pair res; //记录两个素数
for(int i = n / 2; i > 1; i--){ //从n的中间开始找
if(isPrime(i) && isPrime(n - i)){ //第一次遇见两个数都是素数的时候距离从小
cout << i << endl << n - i << endl;
break;
}
}
}
return 0;
}
HJ61 放苹果
描述
把m个同样的苹果放在n个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?
注意:如果有7个苹果和3个盘子,(5,1,1)和(1,5,1)被视为是同一种分法。
数据范围:0≤m≤10 ,1≤n≤10 。
输入描述:
输入两个int整数
输出描述:
输出结果,int型
解法一:dfs
#include
using namespace std;
int dfs(int m, int n) {
if (m == 0) return 1; // 第一种情况,我们的苹果的数量为 0
if (n == 1) return 1; // 第二种情况,我们只剩下了一个盘子
if (m < n) return dfs(m, m); // 如果我们的苹果数量小于了我们的盘子的数量,我们让盘子数量等于苹果的数量
return (dfs(m - n, n) + dfs(m, n - 1)); // 其他情况的时候,我们要计算少一个盘子,和所有盘子拿走一个苹果的情况,最后就是答案
}
void solve() {
int m, n;
while(cin >> m >> n) { // 多组输入我们的 m 和 n
cout << dfs(m, n) << "\n"; // dfs最后返回的就是我们的答案
}
}
signed main()
{
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
solve();
return 0;
}
解法二:动态规划
#include
#include
using namespace std;
const int N = 20;
int dp[N][N], n, m;
// n个盘子,m个苹果,dp[i][j]代表i个苹果,j个盘子有多少种放的方法
void solve() {
while(cin >> m >> n) {
memset(dp, 0, sizeof dp); // 清空我们的这个二维的dp数组
for (int i = 1; i <= n; i++) dp[0][i] = 1; // 把苹果数量为1的,选法置为1
for (int i = 1; i <= m; i++) dp[i][1] = 1; // 把盘子数置为1的,选法置为1
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (i < j) dp[i][j] = dp[i][i]; // 如果盘子数量大于苹果的数量,那么转移方程
else dp[i][j] = dp[i - j][j] + dp[i][j - 1]; // 如果苹果数量大于等于盘子的数量,我们将他们转移为二者相加
}
}
cout << dp[m][n] << "\n"; // 输出最后的答案
}
}
signed main()
{
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
solve();
return 0;
}