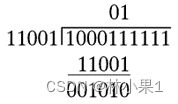计算机算术

计算机算术

数据是什么

数据是各种各样的信息，如数字、文本、计算机程序、音乐、图像、符号等等，实际上，信息可以是能够被计算机存储和处理的任何事物。

位与字节

计算机中存储和处理信息的最小单位是位（Binary digit比特，bit），一个比特的值可以是0或1。

数字计算机将信息以一组或一串比特（称作字）的形式保存在存储器中。如，串01011110表示一个8位的字。

计算机通过高低电压（高低电位）两个电压等级来存储0和1的状态。

计算机通常不会每次只对一个二进制位进行操作，而是对一组二进制位进行操作。

8个二进制位为一个字节（byte），一些计算机制造商用术语“字”表示16位的值，长字表示32位的值，还有一些制造商用字表示32位的值，用半字表示16位的值。

位模式

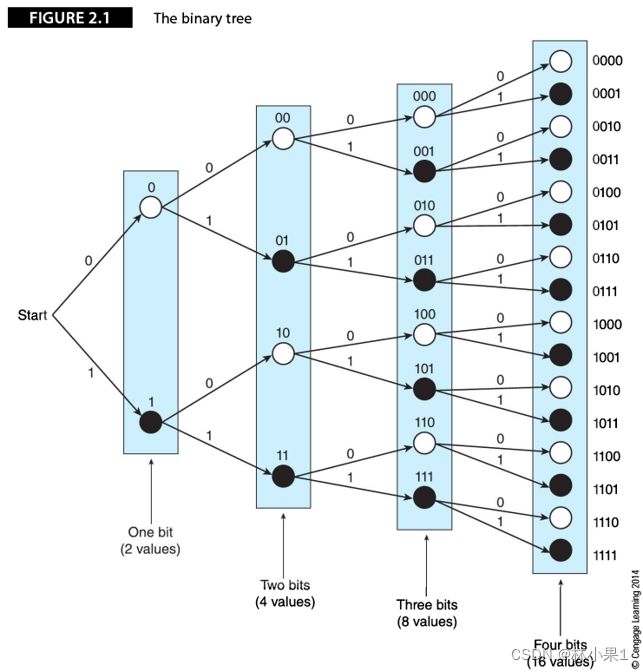
每当数字增加1位，路径的总数将翻一倍。一个n位的字将得到2n条不同路径或位模式。如，一个8位的字节将得到28=256个可能的值。

为了用二进制数表示任何一个拥有最多n个值的量，应找到一个使不等式n<=2m成立的最小位数m。

下图描述了如何用1位、2位、3位和4位得到一个二进制的值序列：

信息表示

一个二进制串可以表示的对象有：

• 指令：

字长为32位或更长的计算机用一个字来表示CPU能够完成的操作（8位或16位计算机用多个字表示一条指令）。指令的二进制编码与其功能之间的关系由计算机设计者决定。如，一台计算机上表示“A加B”的二进制序列可能与另一台计算机上的完全不同。

• 数量：

一个字或多个字都可以用来表示数量。数可以被表示为多种格式，如有符号、无符号二进制整数、二进制浮点数、整数复数等等。

• 字符：

字符是一个叫作“字母表”的集合中元素。拉丁或罗马字母表中的字母、数字字符（A-Z，a-z，0-9）和*、-、+、？等符号都被分配了二进制值，因此可以在计算机内存储和处理。

ASCII码表用7位表示一个字符，一共可以表示27=128个不同的字符。其中96个字符是可打印字符。其余32个是不可打印字符，用于完成回车、退格、换行等特殊功能。

• 图像、声音和视觉：

组成照片的基本单位是像素，每个像素的大小可以是8位（单色）或24位（三基）。

视频作为一串静态图像依次传输，每秒发送60次。

声音通过对波形信号采样。

多媒体信号（如视频、声音）可进行有损压缩。

二进制运算

二进制算术运算规则与十进制基本相同，区别是基数不同。

下面列出了二进制加、减、乘法运算的规则：

两个位相加可能产生进位或借位，和十进制运算规则相同。

下面是4个8位二进制数相加的例子：

当两个二进制数相减时，会从左侧借一位，如：

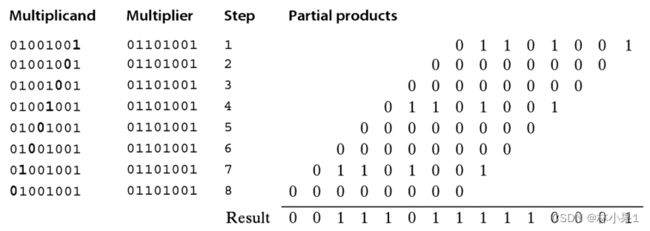
下面描述了01101001（乘数）与01001001（被乘数）相乘的过程，两个n位字相乘将产生一个2n位的积：

有符号整数

负数可以用多种不同的方式表示，计算机设计者选择了3种方法：符号及值表示法、二进制补码表示法、移码表示法，每种方法都有各自的优缺点。

符号及值表示法

一个n位字可以表示从0~2^n-1共2ⁿ个可能的值。如，一个8位的字可以表示0,1，…，254,255。

表示负数的方法是用它的最高位表示符号，通常符号位为0表示正数，符号位为1表示负数。

下面两个8位有符号二进制00001101和10001101的值为：

n位有符号的表示范围为-(2^n-1-1) ~ +(2^n-1-1)。一个8位有符号数的表示-127（11111111）~ +127（01111111）之间的整数。

有人反对该系统的一个原因是它有两个值都表示0：

00000000 = +0 和 10000000 = -0

符号及值表示法没有被用于整数算术运算中，因为它的加、减法运行需要分别用加法器和减法器实现。符号及值表示法用于浮点算术运算中。

二进制补码运算

微处理器用二进制补码系统表示有符号整数，它可以将减法运算转换为对减数的补码的加法运算。

补码的求法：

• 对于正数，其补码就是其本身（其原码）
• 对于负数，其补码是其原码绝对值的二进制表示取反（得到反码）后加1。
• 零的补码只有一种，就是全零。

下面说明了8位二进制数的补码运算过程，将4个数+5、-5、+7、-7转换为补码：

将7与5的补码相加：

结果为9位二进制数100000010。如果忽略最左边一位（进位位），结果为000000102=+2，正是希望得到的结果。

将-7加5：

结果为11111110（进位位为0）。也是希望得到的结果-2，即2⁸-2=100000000-00000010=11111110

用补码运算得出的结果也是补码形式，结果若为正，则无需转换（正数的原码与补码一致），可直接读出结果；若为负，则需将补码转换为原码（原码转换为补码的逆过程），才可读出结果。

补码的特点主要有以下几点：

• 补码的符号位和数值位可以一起参与运算。
• 补码不仅修复了原码和反码的缺陷，而且还可以将加法、减法统一为加法运算，简化了计算机内部的运算电路设计。
• 补码的最大优点是可以直接用于加法运算，使得计算机的硬件实现更为简单。
• 补码的缺点是人们不易直接看出它代表的数值，尤其是对于负数的补码，需要先求出其原码才能知道它代表的实际数值。

乘除法简介

移位运算

进行移位运算时，一个数的所有位都会向左或向右移动一位，如将00101100左移一位，变为01011000，右移一位，变为00010110。有些计算机每次可以移动多位。

移位运算又可以分为逻辑移位和算术移位：

• 逻辑移位：逻辑左移和逻辑右移在移位过程中，都是用0来填充空出的位。逻辑移位只看二进制数值，不考虑其代表的数值的正负，所以逻辑移位适用于无符号数的运算。
• 算术移位：算术左移与逻辑左移没有区别，都是用0填充空出的位。但算术右移在填充空出的位时，会用原来最高位（符号位）的值来填充，即如果原来是正数，那么空出的位就填充0；如果原来是负数，那么空出的位就填充1。算术移位考虑了数值的正负，所以适用于有符号数的运算。

下图描述了算术移位的过程：

a）算术左移：最低位补0，最高位被复制到进位标志中，如11000101左移一位得到10001010。（在不溢出的情况下相当于乘以2）

b）算术右移：最高位补符号位，所有位右移一位。最低位复制到进位标志中，如00100101右移一位得到00010010。11100101右移一位得到11110010。（在不溢出的情况下相当于除以2）

无符号二进制乘法

计算机从乘数的最低位开始，每次检查一位，判断它是否为0，如果乘数的当前位为1则写下被乘数，若该位为0则写下n个0。接下来检查乘数的下一位，这时应从上一位数的左边一位开始写下被乘数或0。被写下的这一组数叫作部分积。得到所有的部分积后，加到一起，得到乘法结果：

乘法结果100000102 = 130是一个8位二进制数。两个二进制数相乘得到一个2n位的积。

但是计算机并没有实现上面的算法，这种算法要求计算机存储n个部分积，然后将它们同时相加。更好的做法是每得到一个部分积就做一次加法。

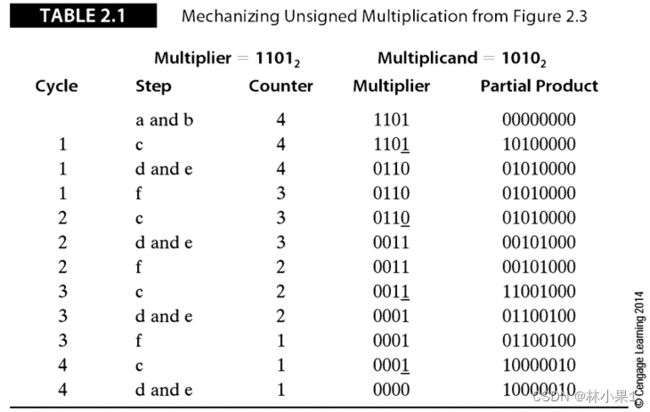
下面给出了一个计算两个n位无符号二进制数相乘的算法：

步骤a：将计数器的值置为n

步骤b：将2n位的部分积寄存器清零

步骤c：检查乘数的最右位（即最低位），将被乘数与部分积的最低位n位相加

步骤d：将部分积右移一位

步骤e：将乘数右移一位（乘数的最右位被丢弃）

步骤f：将计数器的值减1，重复步骤c直到n个周期后计数器的值变为0。部分积寄存器的内容就是乘积结果。

快速乘法

通过移位和加法实现的乘法速度很慢，实际的计算机采用了多种方法加快乘法运算的速度。

快速乘法是一种在计算机科学中用于加速大整数的乘法的算法。这种方法是基于分治策略，把大问题分解成几个相对较小的子问题来解决。

对于两个 n 位的数 a 和 b，我们可以将其分为两个 n/2 位的数，即 a = a1 * 2^(n/2) + a0，b = b1 * 2^(n/2) + b0。那么 a*b = a1*b1*2ⁿ + (a1*b0 + a0*b1)*2^(n/2) + a0*b0。我们需要计算 a1*b1，a1*b0，a0*b1，a0*b0 这四项，然后将结果加起来。但是这样并没有减少计算量，因为我们仍然需要做四次乘法。

然而，通过数学技巧，我们可以将四次乘法减少到三次。这就是所谓的卡拉齐（Karatsuba）算法。该算法是这样进行的：首先计算 a1*b1 和 a0*b0，然后计算 (a1+a0)*(b1+b0)，最后用第三个结果减去前两个结果，得到的就是 a1*b0 + a0*b1。

这样，我们只需要做三次乘法，然后再做一些加法和位移操作，就可以得到结果。

除法

无符号二进制除法的例子：

被除数的前5位比除数小，因此商的最高位为0并将除数与被除数的前6位比较：

被除数的前6位中有一个除数，减法后得到新的部分被除数为001010（1111），将被除数的下一位移下来：

新的部分被除数小于除数，因此商的下一位为0，后续除法过程如下：

除法结果商为10111，余数为0。

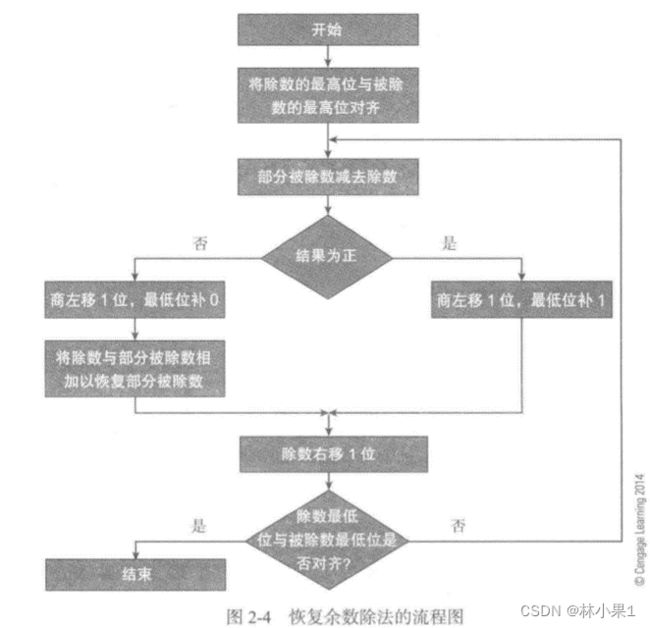
恢复余数除法

刚刚讨论的除法方法，用计算机实现，需要修改的就是除数与部分被除数的比较方法，计算机减去并检测结果的符号位。如果减法的结果为正，则商1，如果结果为负，则商0并将部分被除数与除数相加，将其恢复为原先的值。

恢复余数除法算法：

1）将除数的最高位与被除数的最高位对齐

2）从部分被除数中减去除数，得到新的部分被除数

3）如果新的部分被除数为负数，则商0并用新的部分被除数加上除数，恢复原先的部分被除数

4）如果新的部分被除数为正，则商1

5）判断除法是否结束，如果除数的最低位与部分被除数的最低位对齐，则除法结束，最后的部分被除数就是余数。否则，执行第6步

6）将除数右移一位，从第2步继续执行。

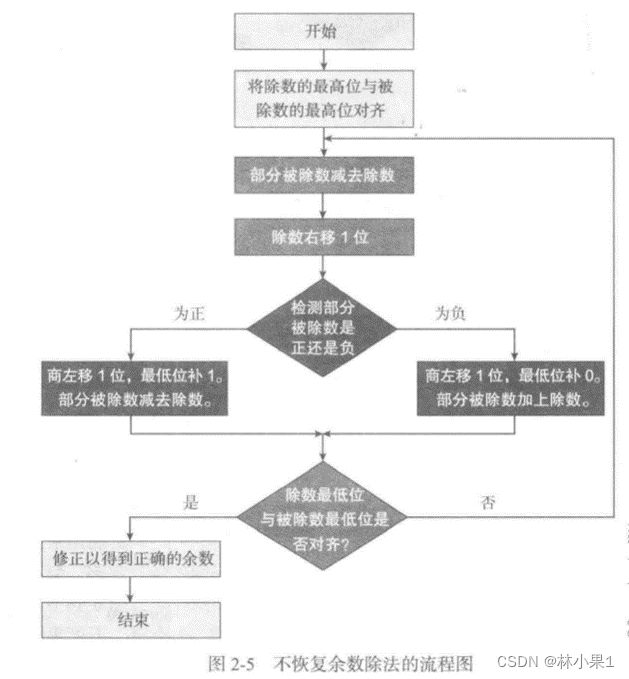
不恢复余数除法

不恢复余数除法是一种在计算机算术中常用的除法方法。这种方法的特点是在每一步中，不需要恢复被除数的余数，而是直接将除法的结果累加到商中。这种方法的优点是计算速度快，效率高，但是需要在开始时就确定除数和被除数的位数。

不恢复余数除法的基本步骤如下：

1. 先将除数左移，使其最高位与被除数的最高位对齐。
2. 然后将对齐后的除数与被除数相减，得到的结果称为“部分余数”。
3. 如果部分余数为正，那么商的当前位就设为1，然后将部分余数左移一位。
4. 如果部分余数为负，那么商的当前位就设为0，然后将被除数（而不是部分余数）左移一位。
5. 重复步骤2-4，直到得到的商的位数等于预定的位数。

这种方法虽然计算速度快，但是如果除数和被除数的位数较大，可能会导致精度损失。因此，在需要高精度计算的场合，可能需要使用其他的除法方法。

浮点数

浮点数即实数，实数是所有有理数和无理数的集合。

之所以叫作浮点数，是因为小数点在数中的位置并不是固定的。一个浮点数值分为两部分存储 ：数值以及小数点在数值中的位置。

计算机中的浮点运算的计算结果一般是不确定的，一块芯片上的浮点计算结果也许与另一块芯片上的不同。

科学计数法：来表示很大或很小的数。

十进制浮点数可以被表示为：尾数x10^指数，如1.2345x10²⁰

二进制浮点数可以被表示为：尾数x2^指数，如1.0111x2⁵

IEEE 754浮点数标准提供3种浮点数表示：32位单精度浮点数、64位双精度浮点数、128位四精度浮点数

规格化浮点数

IEEE 754浮点数的尾数总是规格化的，其范围为1.000…0x2^e到1.111…1x2^e，e为指数。

规格化浮点数的最高位总是1，规格化使尾数的所有位都是有效的，因而尾数精度最高。

如：

0.10…x2^e规格化为1.10…x2^e-1

10.1…2^e规格化为1.01…x2e⁺¹

偏置指数

IEEE 754浮点数的尾数被表示为符号及值的形式，即用一个符号位表示它是正数还是负数。它的指数则用偏置方式表示，即给真正的指数加上一个常数。

假定所用的指数为8位，偏置值为127。如果一个数的指数为0，则被保存为0 + 127=127。如果指数为-2，则被保存为-2 + 127 = 125。

实数1010.1111规格化的结果为+1.010111x2³，指数为+3，将被保存为3+127=130，即130用二进制表示为10000010。

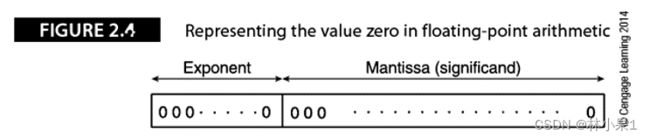
这种用偏置表示指数的方法优点在于，最小的负指数被表示为0，如果不采用这种方法，0的浮点表示为0.0…0x2^{最小负指数}。采用偏置指数，0就可以用尾数0和指数0表示：

IEEE浮点数

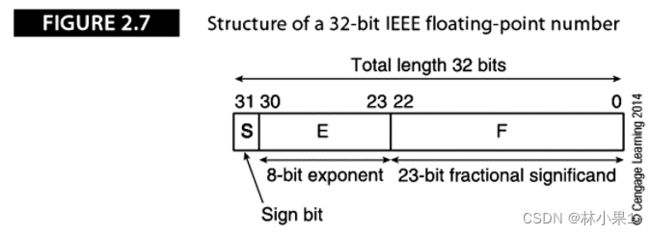
一个32位IEEE 754单精度浮点数可以被表示为下面的二进制串：

S EEEEEEEE 1.MMMMMMMMMMMMMMMMMMMMMMM

S为符号位，指明这个数是正数还是负数

E为8位偏置指数，指出了小数点的位置

M为23位尾数

S位为符号位，决定了数的符号，若S=0，则为正数，若S=1，则为负数。

指数E将浮点数的尾数扩大或缩小2E倍，并且偏置值为127。

如浮点数+1.11001…0x2¹²的指数为12+127=13910=100010112 。

IEEE浮点数的尾数总是规格化的，其值范围在1.0000…00~1.1111…11，除非这个浮点数是0，此时尾数为0.000…00。

由于尾数总是规格化的，且最高位总是为1，因此将尾数存入存储器时没有必要保存最高位的1。所以，一个非0的IEEE 754浮点数可被定义为：

S：符号位

E：偏置量为B的指数

F：尾数的小数部分（实际的尾数为1.F，有个隐含的1）

浮点数0被表示为S=0，E=0，M=0（即浮点数0用全0表示）

考虑下面的例子：

将一个32位IEEE单精度浮点数X=11000001100110011000000000000000解压为一个符号位、一个偏置指数和一个尾数。

解压这3个字段得到：S = 1，E=10000011，F=00110011000000000000000

实际的尾数为1. 00110011000000000000000，因此这个数为：

-1. 00110011000000000000000 x 2^{10000011–01111111}

= -1.00110011000000000000000 x 2⁴

= -10011.0011

IEEE浮点数格式

ANSI/IEEE 745-1985标准定义了基本的和扩展的浮点数格式，以及一组数量有限的算术运算的规则（加、减、乘、除、平方根、求余和比较）。

非数（Not a Number，NaN）是IEEE 754标准提供的一个专门符号，代表IEEE 754标准格式所不能表示的数。

下图，IEEE 754标准定义了3种浮点数格式：

在32位IEEE 754单精度浮点数格式中，最大指数E_max为+127，最小指数E_min为-126，而不是+128~-127。E_min-1（即-127）用来表示浮点0，E_max+1用来表示正/负无穷大或NaN数。

IEEE浮点数的特点

1）浮点数接近0时的特点

下图描述了一个指数为2位，尾数为2位的浮点数系统。浮点数0表示为00 000，下一个规格化的正数表示为00 100（即2^-bx 1.00，b为偏置常量）：

浮点数0附近有一块禁止区，其中的浮点数都是非规格化的，因此无法被表示为IEEE标准格式。这个数的指数和起始位都是0的区域，也可用来表示浮点数。

但是这些数都是非规格化的，其精度比规格化数的进度低，会导致渐进式下溢。

2）IEEE标准规定，缺省的舍入技术应该向最近的值舍入

3）IEEE标准规定了4种比较结果，分别是等于、小于、大于和无序（unordered），无序用于一个操作数是NaN数的情景

4）IEEE标准规定了5种异常：

• 操作数不合法：当程序员使用一些不合法的操作数。如NaN数、与无穷大数相加或相减时、求负数的平方根等
• 除数为0
• 上溢：当结果比最大浮点数还大时。处理上溢的方法有终止计算和饱和运算（用最 大值作为结果）等
• 下溢：当结果比最小浮点数还小时。也就是说，结果小于2Emin。下溢可以通过将 最小浮点数设为0或用一个小于2Emin的非规格化数表示最小浮点数等方式处理
• 结果不准确：当某个操作产生舍入错误时

浮点运算

由于浮点操作数已被表示为规格化形式，在相加时需要对齐指数：

为了对齐指数，计算机必须执行下面步骤：

第1步，找出指数较小的数

第2步，使两个数的指数相同

第3步，尾数相加（或相减）

第4步，如果有必要，将结果规格化

注意：

1）因为指数有时与尾数位于同一个字中，在加法过程开始之前必须将它们分离开（减压缩）

2）如果两个指数的差大于p+1，p为尾数的位数，较小的数由于太小而无法影响较大的数，结果实际就等于较大的数。如，1.1010x2⁶⁰+1.01x2^-12的结果为1.1010x2⁶⁰，因为指数之差为72

3）结果规格化时检查指数范围，以分别检测指数下溢或上溢。指数下溢会导致结果为0，而指数上溢会造成错误。

舍入和截断误差

浮点运算可能引起尾数位数的相加，需要保持尾数位数不变的方法。最简单的技术叫作截断。

如，将0.1101101截断为4位尾数的结果为0.1101。截断会产生诱导误差（即误差是由施加在数上的操作计算所引起的），诱导误差是偏置的，因为截断后的数总比截断前小。

舍入是一种更好的减少数的位数的技术。如果丢弃的位的值大于剩余数最低位的一半，将剩余数的最低位加1。

考虑两个数在小数点后第4位上舍入的例子：

下图描述了舍入机制：

1）最简单的舍入机制是截断或向0舍入。

2）“向最近的数舍入”方法会选择距离该数最近的那个浮点数作为结果。

3）“向正或负无穷大舍入”方法会选择正或负无穷大方向上最近的有效浮点数作为结果。

当要舍入的数位于两个连续浮点数的正中时，IEEE舍入机制选择最低位为0的点（即向偶数舍入）。

浮点运算和程序员

整数操作时精确、可重复的，浮点数操作是不精确的。

考虑表达式z = x²-y²，x、y、z都是实数。可以将表达式视作x²-y²或(x+y)(x-y)计算，整数运算得到相同结果，但浮点数运算可能得到不同结果。(由于舍入机制的存在)

浮点运算中的误差传播

误差传播是指在连续的浮点运算中，前一个操作的误差会影响后续操作的结果。例如，如果你先将两个数字相加，然后将结果乘以第三个数字，那么加法操作的误差就会影响到乘法操作的结果。误差传播可能会放大原始误差，特别是在涉及到大量计算的长公式或算法中。

生成数学函数

生成数学函数，主要是指通过一些特定的数学方法和技术，计算或近似计算出常见的数学函数的值，如三角函数、指数函数、对数函数、幂函数等。

在计算机中，由于硬件的限制，很多数学函数并不能直接进行精确计算，而是需要通过一些特殊的算法进行近似计算。这些算法主要包括以下几种：

1. 直接计算法：对于一些简单的数学函数，如加、减、乘、除等，可以直接通过硬件进行计算。
2. 查表法：对于一些常见的数学函数，如三角函数、指数函数、对数函数等，可以预先计算出一些点的函数值，存储在一个表中，然后通过查表的方式来获取函数值。
3. 泰勒级数展开法：对于一些复杂的数学函数，可以通过泰勒级数展开来进行近似计算。泰勒级数是一种将函数表示为无穷级数的方法，通过计算有限项的和，可以得到函数的近似值。