代码随想录刷题笔记 DAY 22 | 二叉搜索树的最近公共祖先 No.235 | 二叉搜索树中的插入操作 No.701 | 删除二叉搜索树中的节点 No.450
文章目录
-
- Day 22
-
- 01. 二叉搜索树的最近公共祖先(No. 235)
-
- 1.1 题目
- 1.2 笔记
- 1.3 代码
- 02. 二叉搜索树中的插入操作(No. 701)
-
- 2.1 题目
- 2.2 笔记
- 2.3 代码
- 03. 删除二叉搜索树中的节点(No. 450)
-
- 3.1 题目
- 3.2 代码
- 3.3 代码
Day 22
01. 二叉搜索树的最近公共祖先(No. 235)
题目链接
代码随想录题解
1.1 题目
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
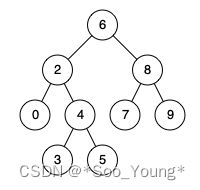
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉搜索树中。
1.2 笔记
二叉搜索树的特点使得二者的公共祖先的节点值一定在所求两点的节点值之间;所以当某一节点的值大于两个节点的时候,所求节点在其左子树(缩小直到在两者之间),反之,所求节点在右子树(增大直到在两者之间)。
比如这个案例,模拟一下遍历的过程
6 > p.val && 6 > q.val2 > p.val && 2 < q.val
由此得出 2 就是要求的结果
看到这里很多朋友会有疑问这个节点一定是结果吗?有没有可能在它的后面呢?
2 > p.val && 2 < q.val 这条语句可以推出 p 在它的左子树, q 在它的右子树,所以如果继续向下遍历的话,得到的就不是公共节点了,所以遍历到的第一个在中间的节点就是所求的节点。
1.3 代码
class Solution {
int pVal;
int qVal;
TreeNode res; // 结果
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
pVal = p.val;
qVal = q.val;
reverse(root);
return res;
}
public void reverse(TreeNode node) {
if (node == null) {
return;
}
if (node.val > pVal && node.val > qVal) {
// 向左查询
reverse(node.left);
} else if (node.val < pVal && node.val < qVal) {
// 向右查询
reverse(node.right);
} else {
//得到结果
res = node;
}
}
}
02. 二叉搜索树中的插入操作(No. 701)
题目链接
代码随想录题解
2.1 题目
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
示例 1:
输入:root = [4,2,7,1,3], val = 5
输出:[4,2,7,1,3,5]
解释:另一个满足题目要求可以通过的树是:
示例 2:
输入:root = [40,20,60,10,30,50,70], val = 25
输出:[40,20,60,10,30,50,70,null,null,25]
示例 3:
输入:root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出:[4,2,7,1,3,5]
提示:
- 树中的节点数将在
[0, 104]的范围内。 -108 <= Node.val <= 108- 所有值
Node.val是 独一无二 的。 -108 <= val <= 108- 保证
val在原始BST中不存在。
2.2 笔记
做本题之前,首先要清楚:
对于任何一个新增的节点都一定能在叶子节点处找到它可以放置的位置
所以这里先确定将这个新增的节点添加到叶子节点就可以减少很多的步骤且更便于理解
确定了方向,先考虑如何 找到所处的位置:从根节点开始遍历,当发现 root.val 大于插入值的时候向 左 遍历,反之则向右遍历,最终一定会遍历到 null 的节点。
而这个位置就是插入的节点所处的位置。
找到这个节点就可以创建一个新的节点并且将其返回,
if (root == null) {
TreeNode node = new TreeNode(val);
return node;
}
在本案例中这个返回值会返回到上一个节点也就是 7 节点的 insertIntoBST(root.left) 中,这时候只需要将 root.left = insertIntoBST(root.left) 就完成了赋值。
本方法的返回值设为 TreeNode,也就是递归的顶层是 root 节点,所以在一层递归中,最终的返回值就是本节点。
梳理一下一层递归中的操作:
- 判断是否为空
- 判断节点值向左或者向右遍历,同时设置节点的
left或right - 将本节点返回
2.3 代码
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
if (root == null) {
TreeNode node = new TreeNode(val);
return node;
}
if (root.val > val) {
root.left = insertIntoBST(root.left, val);
} else if (root.val < val) {
root.right = insertIntoBST(root.right, val);
}
return root;
}
}
03. 删除二叉搜索树中的节点(No. 450)
题目链接
代码随想录题解
3.1 题目
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
- 首先找到需要删除的节点;
- 如果找到了,删除它。
示例 1:
输入:root = [5,3,6,2,4,null,7], key = 3
输出:[5,4,6,2,null,null,7]
解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
示例 3:
输入: root = [], key = 0
输出: []
提示:
- 节点数的范围
[0, 104]. -105 <= Node.val <= 105- 节点值唯一
root是合法的二叉搜索树-105 <= key <= 105
3.2 代码
这道题的难度主要在于考虑全全部可能出现的情况
- 删除节点是非头节点节点的情况
- 删除的是叶子节点
- 删除的是非叶子节点
- 删除节点是头节点的情况
要删除节点首先要找到它,采用搜索二叉树的遍历
if (node.val > ket) {
reverse(node.left);
} else if (node.val < key) {
reverse(node.right);
} else {
// 找到该节点
}
找到该节点后,因为这是要删除的节点,所以上一层应该知道它的 左节点 和 右节点
定义一个全局变量来存储删除节点的左节点和右节点(changeNodeLeft changeNodeRight)
其次,仅仅对于这个的处理只需要 上一层来处理,所以定义一个全局的 boolean 来判断 本层返回后 是否需要删除。
boolean needToChange;
TreeNode changeNodeLeft;
TreeNode changeNodeRight;
这时候当节点返回,以左递归为案例
if (node.val > key) {
reverse(node.left, key);
if (needToChange) {
if (changeNodeLeft == null && changeNodeRight == null) {
// 叶子节点
node.left = null;
} else if (changeNodeLeft == null && changeNodeRight != null) {
node.left = changeNodeRight;
} else if (changeNodeLeft == null && changeNodeRight != null){
node.left = changeNodeLeft;
} else {
node.left = changeNodeLeft;
while (changeNodeLeft.right != null) {
changeNodeLeft = changeNodeLeft.right;
}
changeNodeLeft.right = changeNodeRight;
}
needToChange = false;
}
}
这里要考虑这几种情况
- 左右节点都为空
- 左节点为空但是右节点不为空
- 左节点不为空但是右节点为空
- 左节点和右节点都不为空
对于第一种情况直接将其 node.left 设置为空即可
因为要删除的节点在其左子树,所以要删除的节点的左子树和右子树中的所有节点都一定比本节点小。
这样对于 2 和 3 情况的处理就是将不为空的放到本节点的左子树 node.left
节点的左子树中的所有值一定比右子树中的任何一个值要小
所以如果将左右子树合并的话,右子树一定在左子树的最右边的叶子节点,所以对于情况 4 只需要将右子树置于左子树的最右边的叶子节点,再将左子树的节点放置到 node.left 即可
关系:本节点的值 > 右子树中所有的值 > 左子树中所有的值
由这个关系就可以推断出处理的方法
对于右递归也是同理
else if (node.val < key) {
reverse(node.right, key);
if (needToChange) {
if (changeNodeLeft == null && changeNodeRight == null) {
// 叶子节点
node.right = null;
} else if (changeNodeLeft == null && changeNodeRight != null) {
node.right = changeNodeRight;
} else if (changeNodeLeft == null && changeNodeRight != null){
node.right = changeNodeLeft;
} else {
node.right = changeNodeLeft;
while (changeNodeLeft.right != null) {
changeNodeLeft = changeNodeLeft.right;
}
changeNodeLeft.right = changeNodeRight;
}
needToChange = false;
}
}
然后就是如果头节点是要删除的节点
- 仅有头节点的情况
- 头节点左子树为空,右子树不为空
- 头节点左子树不为,空右子树为空
- 头节点左右子树都不为空
情况 1 直接返回 null
情况 2 和 3 直接返回不为空的子树即可
最后一个情况和上面一样处理,将右子树放到左子树的最右边的节点上,再将左子树返回即可
if (root.val == key) {
TreeNode left = root.left;
TreeNode right = root.right;
if (right == null && left == null) {
return null;
} else if (right != null && left == null) {
return right;
} else if (right == null && left != null) {
return left;
} else {
TreeNode temp = left;
while (temp.right != null) {
temp = temp.right;
}
temp.right = right;
return left;
}
}
3.3 代码
class Solution {
boolean needToChange;
TreeNode changeNodeLeft;
TreeNode changeNodeRight;
public TreeNode deleteNode(TreeNode root, int key) {
if (root == null) {
return null;
}
if (root.val == key) {
TreeNode left = root.left;
TreeNode right = root.right;
if (right == null && left == null) {
return null;
} else if (right != null && left == null) {
return right;
} else if (right == null && left != null) {
return left;
} else {
TreeNode temp = left;
while (temp.right != null) {
temp = temp.right;
}
temp.right = right;
return left;
}
}
reverse(root, key);
return root;
}
public void reverse(TreeNode node, int key) {
if (node == null) {
return;
}
if (node.val > key) {
reverse(node.left, key);
if (needToChange) {
if (changeNodeLeft == null && changeNodeRight == null) {
// 叶子节点
node.left = null;
} else if (changeNodeLeft == null && changeNodeRight != null) {
node.left = changeNodeRight;
} else if (changeNodeLeft == null && changeNodeRight != null){
node.left = changeNodeLeft;
} else {
node.left = changeNodeLeft;
while (changeNodeLeft.right != null) {
changeNodeLeft = changeNodeLeft.right;
}
changeNodeLeft.right = changeNodeRight;
}
needToChange = false;
}
} else if (node.val < key) {
reverse(node.right, key);
if (needToChange) {
if (changeNodeLeft == null && changeNodeRight == null) {
// 叶子节点
node.right = null;
} else if (changeNodeLeft == null && changeNodeRight != null) {
node.right = changeNodeRight;
} else if (changeNodeLeft == null && changeNodeRight != null){
node.right = changeNodeLeft;
} else {
node.right = changeNodeLeft;
while (changeNodeLeft.right != null) {
changeNodeLeft = changeNodeLeft.right;
}
changeNodeLeft.right = changeNodeRight;
}
needToChange = false;
}
} else {
needToChange = true;
changeNodeLeft = node.left;
changeNodeRight = node.right;
}
}
}