【论文精读】EfficientNet
摘要
以往的卷积网络模型通过缩放深度,宽度和图像大小的其中之一或之二来扩大网络以实现更好的结果,但这种思想下经常产生次优的精度和效率的算法。
本文认为通过同时平衡网络宽度、深度、分辨率的缩放倍数来扩大卷积网络,可以达到更好的精度和效率。
框架
优化目标
定义卷积网络层 i i i为:
Y i = F i ( X i ) Y_i=F_i(X_i) Yi=Fi(Xi)
其中 F i F_i Fi是卷积算子, Y i Y_i Yi为输出张量, X i X_i Xi为输入张量。 X i X_i Xi的张量形状为 < H i , W i , C i > l
N = F k ⊙ ⋯ ⊙ F 2 ⊙ F 1 ( X 1 ) = ⊙ j = 1 … k F j ( X 1 ) N=F_k\odot\cdots\odot F_2 \odot F_1(X_1)=\odot_{j=1 \dots k}F_j(X_1) N=Fk⊙⋯⊙F2⊙F1(X1)=⊙j=1…kFj(X1)
ConvNet通常被划分为多个阶段,每个阶段除了第一层卷积执行下采样,其余所有卷积层具有相同的结构,故可将卷积网络定义 s s s阶段网络:
N = ⊙ i = 1 … s F i L i ( X < H i , W i , C i > ) N=\odot_{i=1\dots s}F^{L_i}_i(X_{
其中 F i L i F^{L_i}_i FiLi表示层 F i F_i Fi在 i i i阶段重复 L i L_i Li次, < H i , W i , C i >
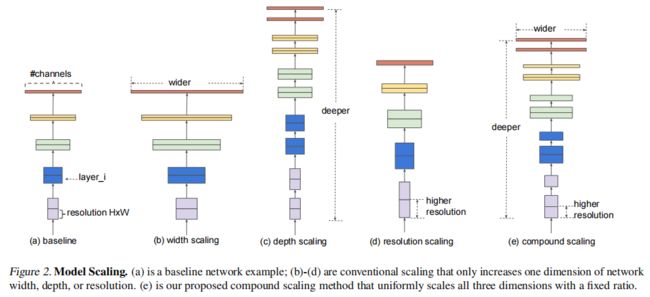
算法目标为找到使网络 N N N最优的深度 L i L_i Li、宽度 C i C_i Ci和分辨率 ( H i , W i ) (H_i,W_i) (Hi,Wi)缩放比,通过在这几个维度缩放网络从而得到最优网络结构,如上图。为了减小搜索空间及节约计算资源,固定 F i F_i Fi,且限制了所有网络层必须以恒定的比例均匀缩放。故优化目标可以定义为对任何给定的资源约束下最大化模型的精度,表述为优化问题为:
max d , w , r A c c u r a c y ( N ( d , w , r ) ) s . t . N ( d , w , r ) = ⊙ i = 1 … s F ˜ i d ⋅ L ˜ i ( X < r ⋅ H ˜ i , r ⋅ W ˜ i , w ⋅ C ˜ i > ) M e m o r y ( N ) ≤ t a r g e t _ m e m o r y F L O P S ( N ) ≤ t a r g e t _ f l o p s \max_{d,w,r} \ Accuracy(N(d,w,r)) \\ s.t. \ \ \ N(d,w,r)=\odot_{i=1\dots s}\~F^{d\cdot \~L_i}_i(X_{
其中 w , d , r w,d,r w,d,r为缩放网络宽/高度、深度、分辨率的系数, F ˜ i , L ˜ i , H ˜ i , W ˜ i , C ˜ i \~F_i,\~L_i,\~H_i,\~W_i,\~C_i F˜i,L˜i,H˜i,W˜i,C˜i为baseline网络的预定义参数,即EfficientNet-B0,具体配置为下图。
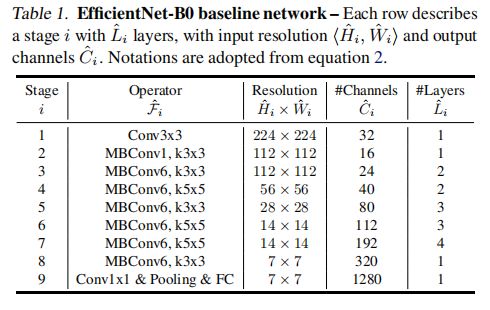
维度缩放
上述优化问题的主要困难在于最优的 w , d , r w,d,r w,d,r相互依赖,且各值在不同的资源约束下都会发生变化,传统的方法主要在其中一个维度上缩放网络,如缩放深度可以使卷积网络捕捉到更丰富、更复杂的特征;缩放宽度可以使卷积网络捕获更细粒度的特征,并且更容易被训练;缩放分辨率可以使卷积网络捕获更细粒度的模式。然而,过深的网络会导致梯度消失问题;过宽但较浅的网络往往难以捕获高层特征;过高的分辨率会导致精度增益降低。
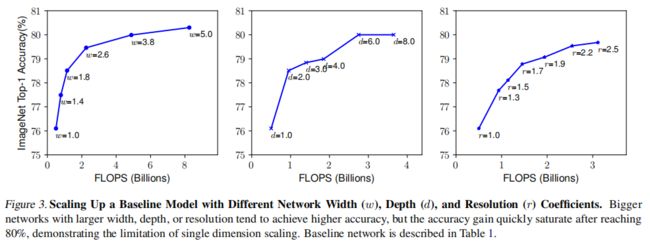
故得出结论,扩展网络宽度、深度或分辨率的任何维度都可以提高精度,但对于较大的模型,精度增益会降低。如上图实验,缩放任一维度都会带来精度提升,但随着倍率的增加,提升会越来越小,直至饱和。
复合缩放

由于不同维度并不独立,故需要协调和平衡不同的缩放维度。上图实验比较了不同网络深度和分辨率下的宽度缩放带来的精度提升。观察到,只扩展网络宽度,精度会迅速饱和。而通过更深的网络和更高的分辨率,宽度扩展在相同的成本下可以获得更好的精度。
故得出结论,为了更高的精度,应当平衡网络宽度、深度和分辨率。定义复合系数 ϕ \phi ϕ平衡网络的宽度、深度和分辨率,则定义:
d e p t h : d = α ϕ w i d t h : w = β ϕ r e s o l u t i o n : r = γ ϕ s . t . α ⋅ β 2 ⋅ γ 2 ≈ 2 α ≥ 1 , β ≥ 1 , γ ≥ 1 depth: \ \ \ d=\alpha^{\phi} \\ width: \ \ \ w=\beta^{\phi} \\ resolution: \ \ \ r=\gamma^{\phi} \\ s.t. \ \ \ \ \alpha \cdot\beta^2 \cdot\gamma^2 \approx 2 \\ \ \ \ \ \ \ \ \ \ \ \alpha \ge 1, \beta \ge 1, \gamma \ge 1 depth: d=αϕwidth: w=βϕresolution: r=γϕs.t. α⋅β2⋅γ2≈2 α≥1,β≥1,γ≥1
其中 α , β , γ α, β, γ α,β,γ是常量,通过网格搜索确定,指定如何将资源分配给网络宽度、深度和分辨率; ϕ \phi ϕ是一个用户指定的系数,控制模型的资源数量。
卷积网络深度加倍时计算量也会加倍,网络宽度或分辨率加倍时计算量会增加四倍,故卷积操作的计算量与 d , w 2 , r 2 d,w^2,r^2 d,w2,r2成正比。由于卷积网络的主要计算成本是卷积运算,故采用上述方程扩展卷积网络将大约增加总计算量(FLOPS) ( α ⋅ β 2 ⋅ γ 2 ) ϕ (\alpha \cdot\beta^2 \cdot\gamma^2)^{\phi} (α⋅β2⋅γ2)ϕ,令 α ⋅ β 2 ⋅ γ 2 ≈ 2 \alpha \cdot\beta^2 \cdot\gamma^2 \approx 2 α⋅β2⋅γ2≈2,则指定混合系数 ϕ \phi ϕ后,网络的计算量大概会是之前的 2 ϕ 2^{\phi} 2ϕ倍。
算法架构
以EfficientNet-B0为baseline,使用 A C C ( m ) × [ F L O P S ( m ) / T ] w ACC(m) \times[FLOPS(m)/T]^w ACC(m)×[FLOPS(m)/T]w作为优化目标,其中 A C C ( m ) ACC(m) ACC(m)和 F L O P S ( m ) FLOPS(m) FLOPS(m)为模型 m m m的精度和计算量, T T T是目标计算量, w = − 0.07 w=-0.07 w=−0.07为控制精度和计算量平衡的超参数。利用多目标神经架构搜索来优化目标,则采用如下复合缩放步骤扩大模型规模:
- 固定 ϕ = 1 ϕ = 1 ϕ=1,假设有两倍以上的可用资源,并根据优化等式2、3对 α , β , γ α, β, γ α,β,γ进行网格搜索。实验发现在 α ⋅ β 2 ⋅ γ 2 ≈ 2 α \cdot β^ 2 \cdot γ^ 2 ≈ 2 α⋅β2⋅γ2≈2的约束下,EfficientNet-B0的最佳值是 α = 1.2 , β = 1.1 , γ = 1.15 α = 1.2, β = 1.1, γ = 1.15 α=1.2,β=1.1,γ=1.15。
- 将 α = 1.2 , β = 1.1 , γ = 1.15 α = 1.2, β = 1.1, γ = 1.15 α=1.2,β=1.1,γ=1.15固定,并利用不同的 ϕ ϕ ϕ及等式3扩展baseline,以获得EfficientNet-B1到B7。
本文方法通过在小的baseline上进行步骤1,然后对所有其他模型使用相同的缩放系数。
实验
对比试验

上图为将EfficientNet应用于MobileNets和的ImageNet的结果,与其他一维缩放方法相比,所提出的复合缩放方法提高了这些模型的精度,表明所提出的方法对一般ConvNets的有效性。

上图实验为从相同的基准EfficientNet-B0扩展的所有EfficientNet模型的性能。EfficientNet在类似精度下比其他ConvNets使用的参数和FLOPS少一个数量级。其中,EfficientNet-B7以66M参数和37B FLOPS实现了84.3%的top1精度,超越了之前最好的GPipe。
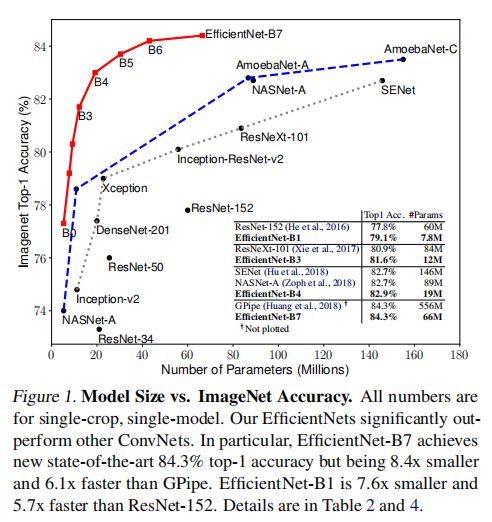
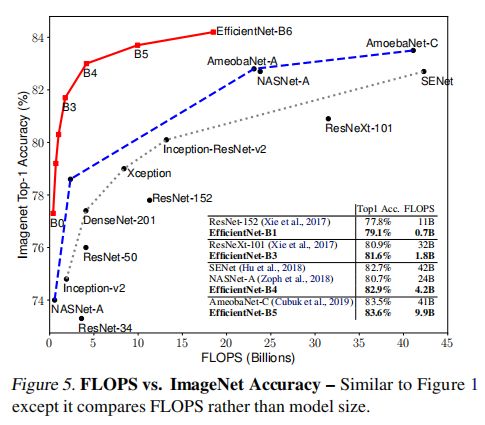
上两图实验了过往最优ConvNets模型的参数/精度和FLOPS/精度曲线,其中EfficientNet比其他ConvNets用更少的参数和FLOPS实现了更好的精度。EfficientNet-B3使用比ResNeXt-101少18倍的FLOPS实现了更高的精度。

上图实验了几个代表性卷积网络在CPU上运行20次的平均推理延迟。EfficientNet-B1比ResNet-152快5.7倍,而EfficientNet-B7比GPipe快6.1倍。这表明EfficientNet具有更快的推理速度。
迁移学习

本实验在常用的迁移学习数据集(详细配置如上图)上实验EfficientNet,所测试的模型在ImageNet预训练checkpoint并在新的数据集上微调。
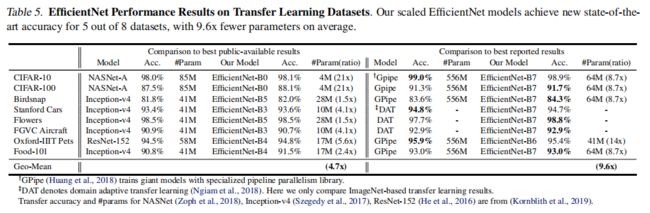
上图显示了迁移学习性能:
- 与NASNet-A等公共模型相比, EfficientNet以减少4.7倍平均(最高21倍)的参数实现了更好的精度
- 与DAT、GPipe等最先进的模型相比,EfficientNet在8个数据集中的5个数据集上超过了它们的精度,但使用的参数少了9.6倍
消融实验

上图比较了各种模型的精度参数曲线。EfficientNets在参数减少了一个数量级的情况下实现了比其他模型更好的精度。

上图比较了不同缩放方法模型的类激活图,所有这些模型都从同一baseline缩放。 观察到,复合缩放的模型倾向于关注更相关、物体细节更多的区域,而其他模型要么缺乏物体细节,要么无法捕捉图像中的所有物体。

上图为不同缩放方法模型的统计数据,对应前面的类激活图。

上图比较了EfficientNet-B0的不同缩放方法在ImageNet训练的模型性能。观察到,所有的缩放方法都以更多的FLOPS为代价来提高精度,但复合缩放方法可以进一步提高精度,比其他一维缩放方法最高可提高2.5%,表明所提出的复合缩放的重要性。
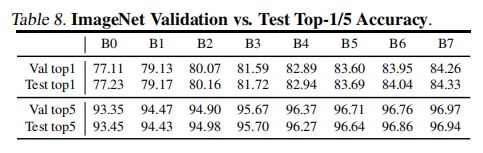
上图实验EfficientNet在ImageNet测试集和验证集上的性能比较,测试集和验证集性能非常接近,证明实验可靠性。
reference
Tan, M. , & Le, Q. V. . (2019). Efficientnet: rethinking model scaling for convolutional neural networks.