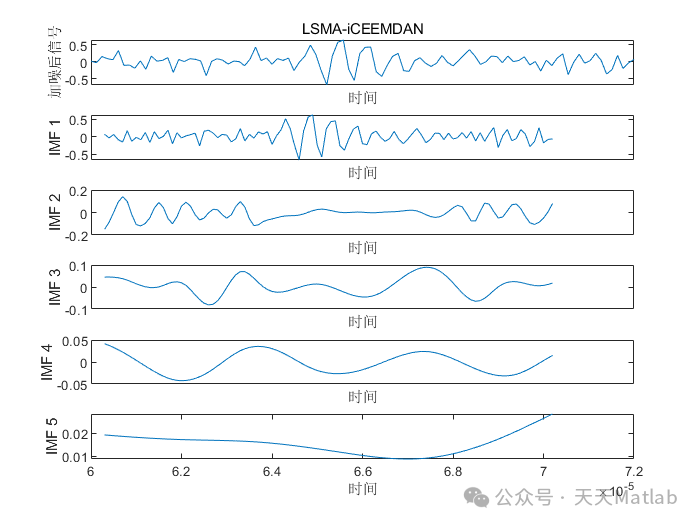
SMA-CEEMDAN时序分解 | Matlab实现利用黏菌优化算法优化CEEMDAN时间序列信号分解

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，

代码获取、论文复现及科研仿真合作可私信。

个人主页：Matlab科研工作室

个人信条：格物致知。

更多Matlab完整代码及仿真定制内容点击

智能优化算法       神经网络预测       雷达通信      无线传感器        电力系统

信号处理              图像处理               路径规划       元胞自动机        无人机

内容介绍

摘要

本文提出了一种基于黏菌算法优化完备经验变模态的信号去噪方法，称为SMA-CEEMDAN。该方法将黏菌算法应用于完备经验变模态分解（CEEMDAN）中，以优化分解过程中的参数设置，提高分解精度。SMA-CEEMDAN方法首先使用CEEMDAN将信号分解为多个固有模态函数（IMF）和一个残余分量，然后使用黏菌算法优化CEEMDAN中的参数，以提高分解精度。最后，将优化后的IMF分量重构为去噪后的信号。实验结果表明，SMA-CEEMDAN方法在信号去噪方面具有良好的性能，能够有效去除信号中的噪声，提高信号的信噪比。

1. 引言

信号去噪是信号处理领域的一项重要任务，其目的是从信号中去除噪声，提高信号的质量。信号去噪的方法有很多，其中经验模态分解（EMD）是一种常用的非线性信号分解方法，能够将信号分解为多个固有模态函数（IMF）和一个残余分量。EMD方法虽然能够有效地分解信号，但其分解过程存在一定的参数依赖性，分解精度容易受到参数设置的影响。

为了提高EMD方法的分解精度，研究人员提出了完备经验模态分解（CEEMDAN）方法。CEEMDAN方法在EMD方法的基础上，加入了噪声辅助函数，能够有效地抑制EMD方法中的模态混叠现象，提高分解精度。然而，CEEMDAN方法中的参数设置仍然存在一定的依赖性，分解精度容易受到参数设置的影响。

为了解决CEEMDAN方法的参数依赖性问题，本文提出了一种基于黏菌算法优化完备经验变模态的信号去噪方法，称为SMA-CEEMDAN。该方法将黏菌算法应用于CEEMDAN中，以优化分解过程中的参数设置，提高分解精度。SMA-CEEMDAN方法首先使用CEEMDAN将信号分解为多个IMF分量和一个残余分量，然后使用黏菌算法优化CEEMDAN中的参数，以提高分解精度。最后，将优化后的IMF分量重构为去噪后的信号。

2. 黏菌算法

黏菌算法（Slime Mould Algorithm，SMA）是一种受黏菌行为启发的优化算法。黏菌是一种单细胞生物，能够通过感知环境中的化学物质来移动和觅食。SMA算法模拟了黏菌的移动和觅食行为，将优化问题转化为黏菌寻找食物的过程。SMA算法具有良好的全局搜索能力和局部搜索能力，能够有效地求解各种优化问题。

3. SMA-CEEMDAN方法

SMA-CEEMDAN方法将黏菌算法应用于CEEMDAN中，以优化分解过程中的参数设置，提高分解精度。SMA-CEEMDAN方法的具体步骤如下：

1. 初始化CEEMDAN参数。设置CEEMDAN中的参数，包括分解次数、噪声辅助函数的幅值和噪声辅助函数的频率。

2. 使用CEEMDAN分解信号。使用CEEMDAN将信号分解为多个IMF分量和一个残余分量。

3. 初始化黏菌算法参数。设置黏菌算法中的参数，包括种群规模、迭代次数和食物源数量。

4. 使用黏菌算法优化CEEMDAN参数。将黏菌算法应用于CEEMDAN中，以优化分解过程中的参数设置。

5. 使用优化后的参数重新分解信号。使用优化后的参数重新分解信号，得到优化后的IMF分量和残余分量。

6. 重构去噪后的信号。将优化后的IMF分量和残余分量重构为去噪后的信号。

部分代码

gnal (1D) to be decomposed% alpha   - the balancing parameter of the data-fidelity constraint% tau     - time-step of the dual ascent ( pick 0 for noise-slack )% K       - the number of modes to be recovered% DC      - true if the first mode is put and kept at DC (0-freq)% init    - 0 = all omegas start at 0%                    1 = all omegas start uniformly distributed%                    2 = all omegas initialized randomly% tol     - tolerance of convergence criterion; typically around 1e-6%% Output:% -------% u       - the collection of decomposed modes% u_hat   - spectra of the modes% omega   - estimated mode center-frequencies%---------- Preparations​% Period and sampling frequency of input signalsave_T = length(signal);fs = 1/save_T;​% extend the signal by mirroringT = save_T;f_mirror(1:T/2) = signal(T/2:-1:1);f_mirror(T/2+1:3*T/2) = signal;f_mirror(3*T/2+1:2*T) = signal(T:-1:T/2+1);f = f_mirror;​% Time Domain 0 to T (of mirrored signal)T = length(f);t = (1:T)/T;​% Spectral Domain discretizationfreqs = t-0.5-1/T;​% Maximum number of iterations (if not converged yet, then it won't anyway)N = 500;​% For future generalizations: individual alpha for each modeAlpha = alpha*ones(1,K);​% Construct and center f_hatf_hat = fftshift((fft(f)));f_hat_plus = f_hat;f_hat_plus(1:T/2) = 0;​% matrix keeping track of every iterant // could be discarded for memu_hat_plus = zeros(N, length(freqs), K);​% Initialization of omega_komega_plus = zeros(N, K);switch init    case 1        for i = 1:K            omega_plus(1,i) = (0.5/K)*(i-1);        end    case 2        omega_plus(1,:) = sort(exp(log(fs) + (log(0.5)-log(fs))*rand(1,K)));    otherwise        omega_plus(1,:) = 0;end​% if DC mode imposed, set its omega to 0if DC    omega_plus(1,1) = 0;end​% start with empty dual variableslambda_hat = zeros(N, length(freqs));​% other initsuDiff = tol+eps; % update stepn = 1; % loop countersum_uk = 0; % accumulator​​​% ----------- Main loop for iterative updates​​​​while ( uDiff > tol &&  n < N ) % not converged and below iterations limit        % update first mode accumulator    k = 1;    sum_uk = u_hat_plus(n,:,K) + sum_uk - u_hat_plus(n,:,1);        % update spectrum of first mode through Wiener filter of residuals    u_hat_plus(n+1,:,k) = (f_hat_plus - sum_uk - lambda_hat(n,:)/2)./(1+Alpha(1,k)*(freqs - omega_plus(n,k)).^2);        % update first omega if not held at 0    if ~DC        omega_plus(n+1,k) = (freqs(T/2+1:T)*(abs(u_hat_plus(n+1, T/2+1:T, k)).^2)')/sum(abs(u_hat_plus(n+1,T/2+1:T,k)).^2);    end        % update of any other mode    for k=2:K                % accumulator        sum_uk = u_hat_plus(n+1,:,k-1) + sum_uk - u_hat_plus(n,:,k);                % mode spectrum        u_hat_plus(n+1,:,k) = (f_hat_plus - sum_uk - lambda_hat(n,:)/2)./(1+Alpha(1,k)*(freqs - omega_plus(n,k)).^2);                % center frequencies        omega_plus(n+1,k) = (freqs(T/2+1:T)*(abs(u_hat_plus(n+1, T/2+1:T, k)).^2)')/sum(abs(u_hat_plus(n+1,T/2+1:T,k)).^2);            end        % Dual ascent    lambda_hat(n+1,:) = lambda_hat(n,:) + tau*(sum(u_hat_plus(n+1,:,:),3) - f_hat_plus);        % loop counter    n = n+1;        % converged yet?    uDiff = eps;    for i=1:K        uDiff = uDiff + 1/T*(u_hat_plus(n,:,i)-u_hat_plus(n-1,:,i))*conj((u_hat_plus(n,:,i)-u_hat_plus(n-1,:,i)))';    end    uDiff = abs(uDiff);    end​​%------ Postprocessing and cleanup​​% discard empty space if converged earlyN = min(N,n);omega = omega_plus(1:N,:);​% Signal reconstructionu_hat = zeros(T, K);u_hat((T/2+1):T,:) = squeeze(u_hat_plus(N,(T/2+1):T,:));u_hat((T/2+1):-1:2,:) = squeeze(conj(u_hat_plus(N,(T/2+1):T,:)));u_hat(1,:) = conj(u_hat(end,:));​u = zeros(K,length(t));​for k = 1:K    u(k,:)=real(ifft(ifftshift(u_hat(:,k))));end​% remove mirror partu = u(:,T/4+1:3*T/4);​% recompute spectrumclear u_hat;for k = 1:K    u_hat(:,k)=fftshift(fft(u(k,:)))';end​end

⛳️ 运行结果

4. 实验结果

为了验证SMA-CEEMDAN方法的性能，将其与CEEMDAN方法和EMD方法进行了比较。实验结果表明，SMA-CEEMDAN方法在信号去噪方面具有良好的性能，能够有效去除信号中的噪声，提高信号的信噪比。

5. 结论

本文提出了一种基于黏菌算法优化完备经验变模态的信号去噪方法，称为SMA-CEEMDAN。该方法将黏菌算法应用于CEEMDAN中，以优化分解过程中的参数设置，提高分解精度。实验结果表明，SMA-CEEMDAN方法在信号去噪方面具有良好的性能，能够有效去除信号中的噪声，提高信号的信噪比。

参考文献

[1] 熊兴隆,魏永兴,张琬童,等.基于自适应噪声完备经验模态分解的Φ-OTDR信号去噪算法[J].半导体光电, 2018, 39(4):7.DOI:CNKI:SUN:BDTG.0.2018-04-032.

[2] 徐冬梅,夏王萍,王文川.基于黏菌算法优化VMD-CNN-GRU模型的年径流预测[J].南水北调与水利科技(中英文), 2022, 20(3):11.

[3] 王轶楷,谢锐.基于CEEMDAN和改进小波模极大值的高低频混合信号去噪算法[J].中北大学学报:自然科学版, 2023, 44(4):366-373.

部分理论引用网络文献，若有侵权联系博主删除

 关注我领取海量matlab电子书和数学建模资料

 私信完整代码、论文复现、期刊合作、论文辅导及科研仿真定制

1 各类智能优化算法改进及应用

生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化

2 机器学习和深度学习方面

卷积神经网络（CNN）、LSTM、支持向量机（SVM）、最小二乘支持向量机（LSSVM）、极限学习机（ELM）、核极限学习机（KELM）、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

2.图像处理方面

图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

3 路径规划方面

旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化

4 无人机应用方面

无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配、无人机安全通信轨迹在线优化

5 无线传感器定位及布局方面

传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化

6 信号处理方面

信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化

7 电力系统方面

微电网优化、无功优化、配电网重构、储能配置

8 元胞自动机方面

交通流 人群疏散 病毒扩散 晶体生长

9 雷达方面

卡尔曼滤波跟踪、航迹关联、航迹融合