嵌入式day10

day9 函数
函数
function //功能 

函数 --- 实现某一个功能的 

函数的定义: //实现函数 

类型标识符 函数名(形式参数)
{
    声明部分
    语句部分
}

(1).类型标识符 (返回值的类型标识符)
   返回值类型 
        返回值 如果没有，返回值类型 一般写成void 
        返回的结果的类型 与 定义返回值类型 不一致 ，以定义的返回值类型为准 
        返回值的类型如果不写，默认为int型 
(2).函数名   --- 一般和函数功能对应 
(3).形式参数 --- 函数接收数据的入口 
    形参 --不是一定要有 
          看函数功能的需要 
          形参没有，一般写成 void 
          
    形参使用时：
    a.个数相同 
    b.类型匹配 
    
    //c.形参 与 实参匹配顺序  -- 在ubunt18.04平台上 顺序是 从 右向左 
     
(4).函数体   --- 完成函数具体功能的代码 

        

函数定义的位置:
1.main函数之前
2.main函数之后
  函数的声明 
  函数头 + 分号 

  函数声明可以放的位置，
  使用之前   
        
        
函数调用的形式:
add(a,b); // 函数调用语句 

int ret;

ret = add(a,b); //函数调用在表达式中 

ret = add(a,b) + 3; //表达式的一部分

//函数调用作为某个函数的实际参数    
printf("sum = %d\n",add(a,b));    

返回值的类型标识符 函数名(形式参数) //函数头 --规定了一下函数的形式   
{
    函数体    //--实现函数具体功能代码 
    
    返回结果 //return 返回结果 
}

strcpy(s1,s2); //实际参数 
    
    
怎么定义函数?

eg:
实现两个数求和?  
a+b  --复用 
1+2     

//功能:
  求和 
  
 准备数据 --> 处理数据 --->输出结果 

y = f(x)  //x --> y
     
 输入数据 -->处理数据 --->带出结果
 
 
  准备数据:
  准备两个数据 --- 形式参数要能接收两个数据 ---本身其实就是变量

  处理数据:
  a+b

  返回结果：
  return 

  
函数名:
  add
  
形式参数:
  int a,b; //形参不能这样写 
  
  数据类型 形参变量名1,数据类型 形参变量名2,...
  
  int a,int b
函数功能:

  a+b
结果:
  return 结果;
  

函数调用:
语法:
  函数名(实际参数);
  
  
练习：
    实现函数，找出两个数中的最大值     
    
    
准备数据:
int a,int b 

处理数据:
 找最大值 
返回结果:
 max 
 
函数名: maxOfTwoNum
形参:  
    int a,int b
函数体:
     a>b
返回值:
    max -- int 返回值的类型 int 

练习:
    找三个数中的最大值 
    
练习:
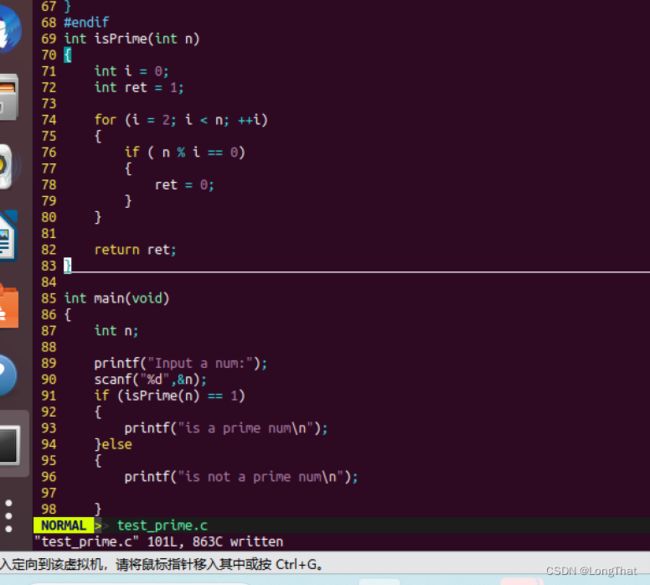
    判断素数?
    
    
    函数功能 --判断 --真 假 
    
    
    
    真 假 
    
    0 ---假 
    1 ---真 //1 
    
main()  //主调函数
{
   add();  //被调函数 
}

练习:
     打印100以内的素数 
    
练习:
    输入月份
    打印月份的天数 
    
    
    printMonthDays()
    {
       if isLeapYear
    }
    
----------------------------

总结:
1.函数实现 
  主要是 代码逻辑 
  
2.流程图 --- 某一个功能块 

3.main函数 
 主逻辑 
 
 针对 每个功能块 画一个流程图 
 
main函数的流程图:
打印月份天数的流程图:
判断闰年的流程图:
4.打印100以内素数 
main -->printPrimeNumIn100-->isPrime  //函数的嵌套调用 

main -->getMonthDays --> isLeapYear   //函数调用的 本质?

栈 --- 数据结构 --先进后出 (FILO) //First In Last out

linux系统上 ，默认情况下 8M ,大小可以调整。

    
栈:
   特点： 
    先进后出 (FILO)
    8M
   主要:
      局部变量 
      
      自动申请 自动释放 
      
      int a; 
堆:
  特点:
    大 
    手动申请，手动释放 
字符串常量区:
  char s[10] = "hello";
  
全局区(静态区)
  全局变量(静态变量)
  
代码区

内存的5个区
   
    
程序 = 代码 + 数据 

函数的嵌套调用：
特殊的嵌套调用 --- 递归 (自己调用自己)
递归 --就是循环

直接递归
间接递归  

while (1)  //死循环 
{
  
}

递归:
 1.
 2.算法 
 
递归的思路，实现代码？

eg:

1+...+100 
int i = 0;
int sum = 0;
while (i <= 100)
{
  sum += i;
}

//1.初始条件
//2.结束条件 
//3.趋于结束的操作 
//4.循环体 

//sum()
递归来实现: //倒着来 

sum(100)
 |--sum(99)+100
     |--sum(98)+99
         |--sum(97)+98
           ...
            |--sum(2)+3
                |--sum(1)+2
                      |--1

   
   
写出代码:
1.递推关系 //重复的 
 第n项 与 第n-1项之间的关系 
2.结束条件 

sum(100) = sum(99)+100
sum(99) = sum(98) + 99

sum(n) = sum(n-1) + n; //

sum(2) = sum(1)+2
sum(1) = 1

sum(2)

sum(n) = 
int sum(int n) //n = 2
{
  if 递归是否结束? (n==1)
  { //结束
    return 1;
  }else // 
  {
    return sum(n-1)+n;
  }
}

1.利用函数找n以内的素数（自己输入n）

2.

利用函数 输入月份输出对应天数 考虑闰年