【初中生讲机器学习】7. 交叉验证是什么?有哪些?怎么实现?来看!
创建时间:2024-02-10
最后编辑时间:2024-02-10
作者:Geeker_LStar
你好呀~这里是 Geeker_LStar 的人工智能学习专栏,很高兴遇见你~
我是 Geeker_LStar,一名初三学生,热爱计算机和数学,我们一起加油~!
⭐(●’◡’●) ⭐ 那就让我们开始吧!
文章目录
- 一、训练集、验证集和测试集
-
- 训练集 Training Set
- 验证集 Validation Set
- 测试集 Test Set
- 三者关系 & 使用方法
- 二、什么是交叉验证
- 三、为什么需要交叉验证
- 四、如何实现交叉验证
-
- 1. Hold-out 交叉验证
-
- 方式
- 优点
- 缺点
- 代码实现
- ⭐2. K 折(K-fold)交叉验证
-
- 方式
- 优点
- 缺点
- 代码实现
- 3. 留一交叉验证
-
- 方式
- 优点
- 缺点
- 代码实现
- 4. 蒙特卡罗交叉验证
-
- 方式
- 代码实现
- 5. 时间序列交叉验证
-
- 方式
- 代码实现
一、训练集、验证集和测试集
emm,看了好几篇文章,貌似这三个概念很容易混淆(尤其是验证集和测试集),所以先在这里讲明白。
一句话:训练集用于训练模型,验证集用于调整模型超参数并选择合适模型,而测试集用于评估模型性能。验证集 ≠ 测试集!
训练集 Training Set
很明显,训练集就是用于训练模型的数据。
拿中考举例,参加中考之前我们要做无数的作业练习,我们就是模型,作业题就是训练集。
一般来讲,训练集在总数据集中占的比例应该在 70% 左右。过多会造成过拟合,过少会造成欠拟合,都不利于模型的泛化。
验证集 Validation Set
验证集是个易被忽视 or 错用的概念。
还是中考的例子,在正式中考之前,我们还要参加零模一模二模三模…这些考试就是在 “验证” 用测试集训练的成果,但是又不是真正的 “测试”。
和模拟考试一样,验证集的目的是在正式用测试集评估模型之前,大致了解模型的性能并调整模型的一些参数(超参数,后面会讲),最终获得(一定范围内)性能最优的模型,进行测试。
测试集 Test Set
中考就是测试集嘛,就是在用训练集训练 & 验证集调参后,对模型性能的最终评估。测试集并不用于调整任何参数或进行任何优化。
想起了一句特别形象的至理名言:除了中高考以外的所有考试都是检测性考试(验证集),寄了没大事,后面还能调整,而中高考是选拔性考试(测试集),寄了就真寄了((
三者关系 & 使用方法
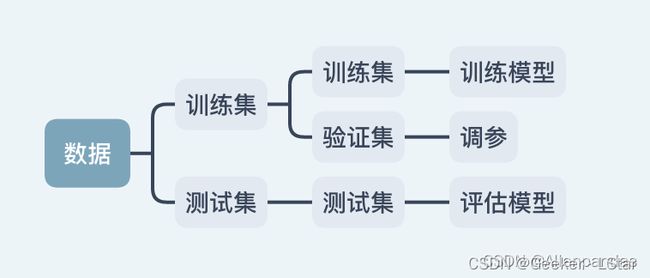
一句话:训练集 -> 模型训练 -> 验证集 -> 超参数调整 -> 最终模型 -> 合并再训练 -> 测试集 -> 最终性能评估。
一般来讲,拿到一个数据集,要先把测试集分出来(大概 10%-20% 左右吧,看数据量有多少了),这部分数据不参与训练 & 验证的过程,从而保证测试数据全部都是未知数据,不会出现模型对某个测试数据特别熟悉的情况,更能看出模型的 “真实水平”(就像中考题永远找不到某某练习册或模拟的原题一样)。
划分完测试集,把剩下数据的 20% 左右(一样,看数据量)再分出来,作为验证集。训练之后先用验证集验证,如果效果不好,可以考虑调整模型的各种超参数。
这个 “调整超参数” 是怎么个事呢?就比如,对于支持向量机,我可以选择不同的核函数(也就是超参数),linear、poly、rbf 之类的,but 我事先并不知道哪种核函数效果最好,于是我可以先选一种,比如 linear,训练一下,再用验证集验证一下效果,发现效果不太好,于是我换一个核函数比如 poly 试试,诶发现效果还是不理想,那我再换用 rbf,发现这次效果好了,就说明最适合这个实例的核函数是径向基函数 rbf。
ok,然后超参数调整好了,找到最合适的模型了,再把训练集和验证集都合并为训练集,进行一次训练,最后用测试集进行测试,评价模型的性能。
概括为下图。
二、什么是交叉验证
一句话:交叉验证是一种评估并有利于提高机器学习模型性能的技术。
交叉验证通常把数据集分为多个子集,一部分用于训练模型(训练集),一部分用于验证 & 调参(验证集,在部分交叉验证方式中可能没有),另一部分用于(测试集)。训练+验证这个过程会重复多次,每次用于训练和验证的数据都不一样,从而得到多个独立的模型性能评估结果。通过这种方式可以优化模型参数,减少过拟合或欠拟合的发生,最终提高模型的泛化能力。
三、为什么需要交叉验证
一句话:交叉验证是为了寻找最适合的超参数,检测并提高模型的泛化能力。
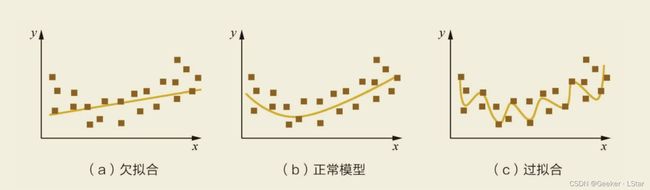
简单来讲,我们现在有很多的训练数据,在不断训练的过程中,模型为了在这些训练数据上获得好的表现,会逐步调整参数来靠近这些训练数据,但这就会导致过拟合的出现,如下图中 “过拟合”。
通过图也能看出来,过拟合并不是什么好事。因为即使模型在训练数据上达到了 100% 的正确,它在新数据上的表现也不会很好,也就是它的泛化能力不强。
but,模型总归还是要用在未知数据上的,所以我们要防止过拟合的情况出现。也就是说,当我们用一批数据训练出了一个模型,必然要用另一批数据来检验一下这个模型的泛化能力,并且最好多次换用不同的数据进行训练 & 验证,最大限度地减少过拟合/欠拟合发生的可能。
同时,很多模型是有超参数的,手动 “试” 这些超参数会非常麻烦,我们可以通过交叉验证的方式,看超参数的不同取值下的模型性能,进而确定超参数要取哪个值。
这就是要进行交叉验证的原因,细节后面会详细讲。
四、如何实现交叉验证
1. Hold-out 交叉验证
方式
Hold-out 交叉验证是最简单的一种方式,它只是把原始数据集随机分成两部分,一般是训练集 70%(+),测试集 30%(-),在训练集上训练过后用测试集进行测试。
严格来讲,Hold-out 验证都不能被称为 “交叉验证”,因为它其实不涉及到数据的 “交叉使用”,它只进行一次训练和一次测试。
下图第二行说明了 Hold-out 训练的形式。
优点
- 训练成本低、速度快
由于 Hold-out 验证只需要进行一次训练+测试,所以它用起来很简单、速度很快,适用于数据量很大的情况。
缺点
- 不太适合用于正负样本不平衡的数据集中。
原因:举一个极端的例子,一个数据集中有 80% 正样本,20% 负样本,如果在随机划分的时候训练集里全是正样本,测试集里全是负样本,这事就很难办了。
这种问题可以通过多次随机划分数据集来解决,但 hold-out 划分只随机划分一次,偶然性高,有可能遇到这种情况。 - 不太适合用于样本量小的数据集中。
原因:样本量不大的时候,每一个样本都很重要。选取 30% 的数据作为测试集(即这部分数据没有被训练到)可能会让模型错过一些重要的特征,出现欠拟合。
代码实现
以鸢尾花数据集和逻辑回归算法为例,实现 hold-out 验证。
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
iris = load_iris()
X = iris.data
Y = iris.target
print("Size of Dataset {}".format(len(X)))
logreg = LogisticRegression()
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.3, random_state=218)
logreg.fit(x_train, y_train)
predict = logreg.predict(x_test)
# 训练集准确率
print("Accuracy score on training set is {}".format(accuracy_score(logreg.predict(x_train),y_train)))
# 测试集准确率
print("Accuracy score on test set is {}".format(accuracy_score(predict,y_test)))
⭐2. K 折(K-fold)交叉验证
一句话:K 折交叉验证主要用于模型超参数的调整,即模型调优。
方式
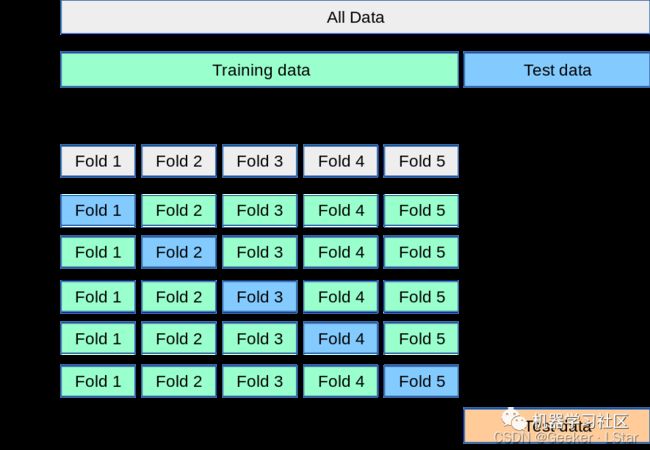
K-fold 交叉验证首先分出测试集,再把剩下的数据随机平均分为 k 组,每一组都是一个 “折叠”(所以叫 K 折嘛)。
在进行训练 & 验证时,k 组中的每一组都会当一次验证集,剩下的 (k-1) 组当训练集,一共会进行 k 次训练 & 验证。k 轮过后再用测试集进行最终评估。
不过有一个要注意的小细节:第 n 折的训练不是在第 n-1 折训练的基础上进行的,相当于每一次训练前都会初始化模型参数。
下图说明了 K-fold 交叉验证的方式。
在实际训练中,一般会分为 10 个折叠,也被称为 10 折交叉验证。
除了防止过拟合,K 折法另一大作用是选择最适合的超参数值(核函数的例子),提高模型性能,过程如下:
选取参数的第一个值 A,进行 k 次训练 & 验证,将 k 次验证的准确率(或其它指标)的平均值作为 A 参数下的模型性能。再取参数的第二个值 B,重复上述过程,得到 B 参数下的模型性能。以此类推,得到同一参数的不同取值(比如核函数中的 linear、poly、rbf)下的模型性能。哪个取值下模型表现好,就用哪个值作为该参数的最终值。
优点
- K 折交叉验证是最常用的交叉验证方式。它可以用于选择最合适的超参数。
- k 次中每次都用不同的数据进行训练 & 测试,可以避免过拟合或欠拟合,提高模型的泛化能力。
- 对于小规模数据,K 折交叉验证相当于反复给它提供不同的验证数据,从一定程度上缓解了样本量不够的问题。
缺点
- 不太适合用于时间序列数据中。
对于时间序列数据,样本顺序很重要,但 K 折交叉验证的样本是随机划分的。 - 训练成本较高,时间较长
很好理解,如果要选择某一个参数的最优值,要进行(取值数 * k)次训练。
代码实现
还是利用鸢尾花数据集 & 逻辑回归算法实现 K-fold 交叉验证。
from sklearn.datasets import load_iris
from sklearn.model_selection import cross_val_score, KFold
from sklearn.linear_model import LogisticRegression
iris = load_iris()
X = iris.data
y = iris.target
logreg = LogisticRegression()
kf = KFold(n_splits = 5) # 划分 5 个折叠
# cross_val_score() 函数负责进行交叉验证并计算交叉验证(5 次)的得分
score = cross_val_score(logreg, X, y, cv=kf)
# 交叉验证准确率
print("Cross Validation Scores are {}".format(score))
# 平均准确率
print("Average Cross Validation score :{}".format(score.mean()))
结果是这样的:
![]()
3. 留一交叉验证
一句话:留一法是验证集只有一个样本的 K 折法。
方式
emmm,其实留一法就是 K 折法的一个特例——让 k 值等于刨除测试集后的数据集中数据的个数,每次用一个样本作为测试集(留一),其它样本作为训练集。就像这样:
优点
- 适合样本量小的数据集
对于样本量小的数据集,每一个数据都很关键,使用留一法可以有效避免模型错过某些重要特征(之前在讲 Hold-out 的缺点时提到过)。
缺点
- 训练成本较高,耗时较长
代码实现
利用鸢尾花数据集和随机森林算法实现留一交叉验证。
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import LeaveOneOut, cross_val_score
iris = load_iris()
X = iris.data
y = iris.target
loo = LeaveOneOut() # 留一法函数
tree = RandomForestClassifier(n_estimators=10, max_depth=5, n_jobs=-1)
score=cross_val_score(tree, X, y, cv=loo)
# 交叉验证准确率
print("Cross Validation Scores are {}".format(score))
# 交叉验证平均准确率
print("Average Cross Validation score :{}".format(score.mean()))
4. 蒙特卡罗交叉验证
emm 这貌似不太常用诶不过还是讲一下吧。
方式
和 K 折或留一法不同,蒙特卡罗交叉验证并不一定要 “随机平均分不同的折”,也不用 “一次一折” 地训练。它允许我们自由决定要用做训练集和验证集的百分比,自由决定训练次数,同时训练集和验证集的百分比加起来不需要是 100%。
比如,我们有 100 个样本,其中 60% 的样本用作训练集,20% 的样本用作验证集,那么剩下的 20% 将不被使用,这种形式重复 n 次。
代码实现
利用鸢尾花数据集和逻辑回归算法实现蒙特卡罗交叉验证。
from sklearn.model_selection import ShuffleSplit,cross_val_score
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression()
shuffle_split = ShuffleSplit(test_size=0.3,train_size=0.5,n_splits=10)
scores=cross_val_score(logreg, iris.data, iris.target, cv=shuffle_split)
print("cross Validation scores:n {}".format(scores))
print("Average Cross Validation score :{}".format(scores.mean()))
5. 时间序列交叉验证
一句话:时间序列交叉验证专门用于处理在不同时间点(时间序列)收集的数据。
方式
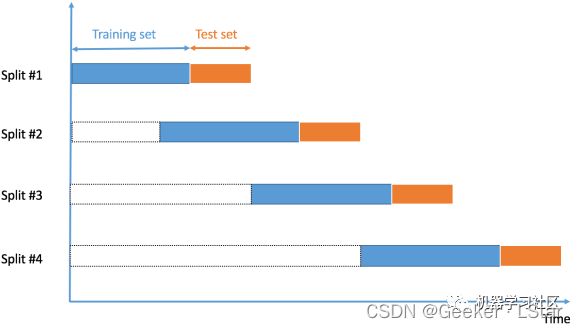
“时间序列数据” 就是在不同时间点收集的数据。由于样本是在相邻时间段收集的,因此样本之间可能存在相关性。在这种情况下,我们不能随机选择样本并将它们分配给训练集或验证集,因为这会破坏样本之间(可能存在)的相关性,同时,使用未来数据的值去预测过去数据的值是没有意义的。
so,这种时候,我们需要根据时间顺序将数据拆分为训练集和验证集,也称为 “前向链” 方法或滚动交叉验证。先用一小部分样本作为训练集,预测稍后的样本的值,检查准确性。再将预测样本作为下一个训练数据集的一部分,对后续样本进行预测,以此类推。
大概是这样的:
代码实现
这个只能自造数据了((
import numpy as np
from sklearn.model_selection import TimeSeriesSplit
X = np.array([[1, 2], [3, 4], [1, 2], [3, 4], [1, 2], [3, 4]])
y = np.array([1, 2, 3, 4, 5, 6])
time_series = TimeSeriesSplit()
print(time_series) # 时间序列
for train_index, test_index in time_series.split(X):
print("TRAIN:", train_index, "TEST:", test_index)
X_train, X_test = X[train_index], X[test_index]
y_train, y_test = y[train_index], y[test_index]
ok!!以上就是机器学习中的各种交叉验证方法,其中 K 折法最常用。
这篇文章讲了机器学习中的各种交叉验证方法(方式+优缺点+代码实现),希望对你有所帮助!⭐
欢迎三连!!一起加油!
——Geeker_LStar