我在代码随想录|写代码Day26 |回溯算法|491.递增子序列 , 46.全排列 , 47.全排列 II

学习目标：

博主介绍: 27dCnc
专题 : 数据结构帮助小白快速入门

☆*: .｡. o(≧▽≦)o .｡.:*☆

---

学习时间：

• 周一至周五晚上 7 点—晚上9点
• 周六上午 9 点-上午 11 点
• 周日下午 3 点-下午 6 点

---

主题: 回溯算法

今日份打卡

• 代码随想录-回溯算法

---

学习内容：

1. 递增子序列
2. 全排列
3. 全排列 II

---

内容详细

491.递增子序列

题目考点: 回溯 回溯算法条件判断

题目思路

这个递增子序列比较像是取有序的子集。而且本题也要求不能有相同的递增子序列。

这又是子集，又是去重，是不是不由自主的想起了刚刚讲过的 90.子集II 。

就是因为太像了，更要注意差别所在，要不就掉坑里了！

在 90.子集II 中我们是通过排序，再加一个标记数组来达到去重的目的。

而本题求自增子序列，是不能对原数组进行排序的，排完序的数组都是自增子序列了。

所以不能使用之前的去重逻辑！

本题给出的示例，还是一个有序数组 [4, 6, 7, 7]，这更容易误导大家按照排序的思路去做了。

为了有鲜明的对比，我用[4, 7, 6, 7]这个数组来举例，抽象为树形结构如图：

通过回溯三部曲分析题目
回溯模版

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

详细请看文章 : 回溯算法基础

最终代码

class Solution {
private:
    vector<int>v;
    vector<vector<int>>result;
public:
    void backtracking(vector<int>&nums,int StratIndex) {
        if(v.size() > 1) {
            result.push_back(v);
        }

        unordered_set<int> uset;
        for (auto i = StratIndex; i< nums.size(); i++) {
            if ((!v.empty() && nums[i] < v.back()) || uset.find(nums[i]) != uset.end()) {
                continue;
            }
            uset.insert(nums[i]);
            v.push_back(nums[i]);
            backtracking(nums,i+1);
            v.pop_back();
        }
    }
public:
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        result.clear(),v.clear();
        backtracking(nums,0);
        return result;
    }
};

对于已经习惯写回溯，看到递归函数上面的 uset.insert(nums[i]);，下面却没有对应的pop之类的操作，很不习惯

这也是需要注意的点，unordered_set uset; 是记录本层元素是否重复使用，新的一层uset都会重新定义（清空），所以要知道uset只负责本层！

46.全排列

题目考点: 全排列 回溯

常规操作

思路

此时我们已经学习了77.组合问题 、 131.分割回文串 和 78.子集问题 ，接下来看一看排列问题。

相信这个排列问题就算是让你用for循环暴力把结果搜索出来，这个暴力也不是很好写。

因为一些问题能暴力搜出来就已经很不错了！

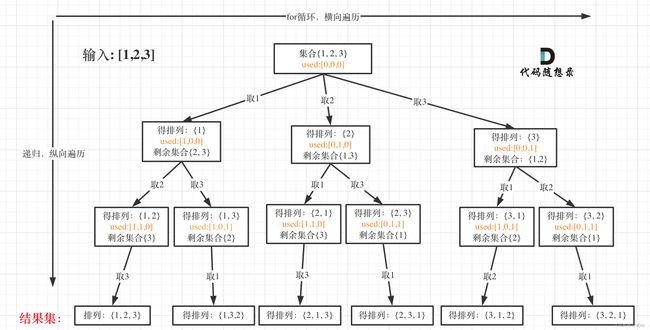
我以[1,2,3]为例，抽象成树形结构如下：

然后就是递归三部曲

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

最终代码

class Solution {
public:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking (vector<int>& nums, vector<bool>& used) {
        // 此时说明找到了一组
        if (path.size() == nums.size()) {
            result.push_back(path);
            return;
        }
        for (int i = 0; i < nums.size(); i++) {
            if (used[i] == true) continue; // path里已经收录的元素，直接跳过
            used[i] = true;
            path.push_back(nums[i]);
            backtracking(nums, used);
            path.pop_back();
            used[i] = false;
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        result.clear();
        path.clear();
        vector<bool> used(nums.size(), false);
        backtracking(nums, used);
        return result;
    }
};

非常规写法

class Solution {
public:
    vector<vector<int>> permute(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        vector<vector<int>>result;
        do {
            result.push_back(nums);
        } while(next_permutation(nums.begin(),nums.end()));
        return result;
    }
};

47.全排列 II

题目考点 : 回溯 全排列

题目图解

然后便是回溯三部曲

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

最终代码

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking (vector<int>& nums, vector<bool>& used) {
        // 此时说明找到了一组
        if (path.size() == nums.size()) {
            result.push_back(path);
            return;
        }
        for (int i = 0; i < nums.size(); i++) {
            // used[i - 1] == true，说明同一树枝nums[i - 1]使用过
            // used[i - 1] == false，说明同一树层nums[i - 1]使用过
            // 如果同一树层nums[i - 1]使用过则直接跳过
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
                continue;
            }
            if (used[i] == false) {
                used[i] = true;
                path.push_back(nums[i]);
                backtracking(nums, used);
                path.pop_back();
                used[i] = false;
            }
        }
    }
public:
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        result.clear();
        path.clear();
        sort(nums.begin(), nums.end()); // 排序
        vector<bool> used(nums.size(), false);
        backtracking(nums, used);
        return result;
    }
};

// 时间复杂度: 最差情况所有元素都是唯一的。复杂度和全排列1都是 O(n! * n) 对于 n 个元素一共有 n! 中排列方案。而对于每一个答案，我们需要 O(n) 去复制最终放到 result 数组
// 空间复杂度: O(n) 回溯树的深度取决于我们有多少个元素

拓展

大家发现，去重最为关键的代码为：

if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
    continue;
}

如果改成 used[i - 1] == true， 也是正确的!，去重代码如下：

if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
    continue;
}

这是为什么呢，就是上面我刚说的，如果要对树层中前一位去重，就用used[i - 1] == false，如果要对树枝前一位去重用used[i - 1] == true。

对于排列问题，树层上去重和树枝上去重，都是可以的，但是树层上去重效率更高！

这么说是不是有点抽象？

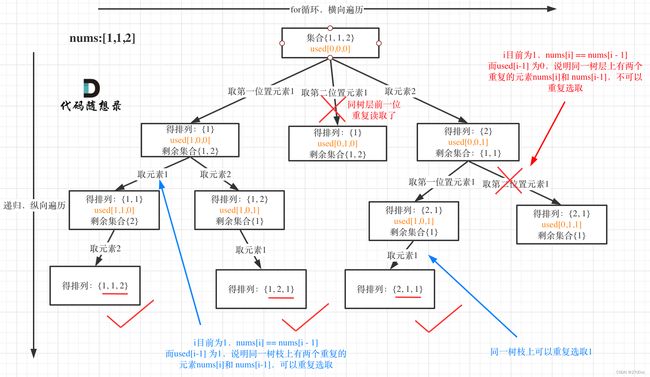
来来来，我就用输入: [1,1,1] 来举一个例子。

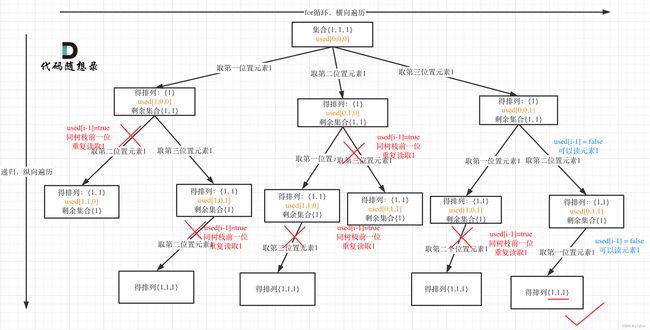
树层上去重(used[i - 1] == false)，的树形结构如下：

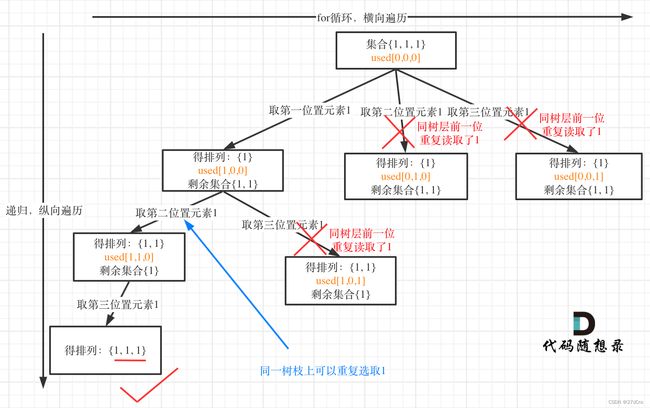
树枝上去重（used[i - 1] == true）的树型结构如下：

大家应该很清晰的看到，树层上对前一位去重非常彻底，效率很高，树枝上对前一位去重虽然最后可以得到答案，但是做了很多无用搜索。

非常规方法

class Solution {
public:
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        vector<vector<int>>result;
        do {
            result.push_back(nums);
        } while(next_permutation(nums.begin(),nums.end()));
        return result;
    }
};

对于非常规方法不理解的可以看我的: STL库 了解函数

其他语言版本

Java

class Solution {
    //存放结果
    List<List<Integer>> result = new ArrayList<>();
    //暂存结果
    List<Integer> path = new ArrayList<>();

    public List<List<Integer>> permuteUnique(int[] nums) {
        boolean[] used = new boolean[nums.length];
        Arrays.fill(used, false);
        Arrays.sort(nums);
        backTrack(nums, used);
        return result;
    }

    private void backTrack(int[] nums, boolean[] used) {
        if (path.size() == nums.length) {
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i < nums.length; i++) {
            // used[i - 1] == true，说明同⼀树⽀nums[i - 1]使⽤过
            // used[i - 1] == false，说明同⼀树层nums[i - 1]使⽤过
            // 如果同⼀树层nums[i - 1]使⽤过则直接跳过
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
                continue;
            }
            //如果同⼀树⽀nums[i]没使⽤过开始处理
            if (used[i] == false) {
                used[i] = true;//标记同⼀树⽀nums[i]使⽤过，防止同一树枝重复使用
                path.add(nums[i]);
                backTrack(nums, used);
                path.remove(path.size() - 1);//回溯，说明同⼀树层nums[i]使⽤过，防止下一树层重复
                used[i] = false;//回溯
            }
        }
    }
}

Python

class Solution:
    def permuteUnique(self, nums):
        nums.sort()  # 排序
        result = []
        self.backtracking(nums, [], [False] * len(nums), result)
        return result

    def backtracking(self, nums, path, used, result):
        if len(path) == len(nums):
            result.append(path[:])
            return
        for i in range(len(nums)):
            if (i > 0 and nums[i] == nums[i - 1] and not used[i - 1]) or used[i]:
                continue
            used[i] = True
            path.append(nums[i])
            self.backtracking(nums, path, used, result)
            path.pop()
            used[i] = False

Go

var (
    res [][]int
    path  []int
    st    []bool   // state的缩写
)
func permuteUnique(nums []int) [][]int {
    res, path = make([][]int, 0), make([]int, 0, len(nums))
    st = make([]bool, len(nums))
    sort.Ints(nums)
    dfs(nums, 0)
    return res
}

func dfs(nums []int, cur int) {
    if cur == len(nums) {
        tmp := make([]int, len(path))
        copy(tmp, path)
        res = append(res, tmp)
    }
    for i := 0; i < len(nums); i++ {
        if i != 0 && nums[i] == nums[i-1] && !st[i-1] {  // 去重，用st来判别是深度还是广度
            continue
        }
        if !st[i] {
            path = append(path, nums[i])
            st[i] = true
            dfs(nums, cur + 1)
            st[i] = false
            path = path[:len(path)-1]
        }
    }
}

---

学习产出：

• 技术笔记 2 遍
• CSDN 技术博客 3 篇
• 习的 vlog 视频 1 个

如果此文对你有帮助的话，欢迎关注、点赞、⭐收藏、✍️评论，支持一下博主~