插值（二）——拉格朗日插值（C++）

问题的提出

假设只有两个插值点：$x_0,x_1;y_0,y_1$，求$P_1(x)=a_0+a_{1}x$使得$P_1(x_0)=y_0,P_1(x_1)=y_1$，由此可以得到$$\begin{array}{rl}{P}_1(x)& =y_0+\frac{y_1-y_0}{x_1-x_0}(x-x_0)\\ & =\frac{x-x_1}{x_0-x_1}{y}_0+\frac{x-x_0}{x_1-x_0}{y}_1\\ & =\sum _{i=0}^1{l}_i{y}_i\end{array}$$
这是对于只有两个插值点的情况，现在对其拓展到任意个插值点。

拉格朗日插值法

对于给出的n个插值坐标：$x_0,x_1\cdots x_n;y_0,y_1\cdots y_n$，构造插值函数$P_n(x)={\sum }_{i=0}^n{l}_i(x)y_i$，显然$P_n(x_i)=y_i$，所以有$$\{\begin{array}{l}{l}_i(x_i)=1\\ l_i(x_j)=0(i\ne j)\end{array}$$
因此构造出$$l_i(x)=\prod _{j=0,j\ne i}^n\frac{x-x_j}{x_i-x_j}$$
代入原式，得到$$L_n(x)=\sum _{i=0}^n{l}_i(x)y_i$$
对应的$l_i(x)$被称为拉格朗日插值基函数。

代码实现

//拉格朗日插值法
#include
#include
//拉格朗日插值法，输入插值点坐标、需要求值的x和插值点数n
double Lagrange(double *xi,double *yi,double x,int n)
{
    double Ln = 0;
    for (int i = 0; i < n;i++)
    {
        double li = 1.0;
        for (int j = 0; j < n;j++)
        {
            if(i!=j)
            {
                li*=((x-xi[j])/(xi[i]-xi[j]));    
            }
        }
        Ln+=yi[i]*li;
    }
    return Ln;
}
double fx(double x)
{
    return sqrt(x + 3);
}
int main()
{
    int n;
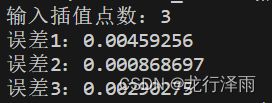
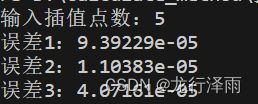
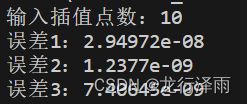
    std::cout << "输入插值点数：";
    std::cin>>n;
    double *x = new double[n];
    double *y = new double[n];
    double error[3]={0.0f,0.0f,0.0f};//误差评价
    double a = 3, b = 10;//插值区间
    for(int i=0;ierror[0])
        {
            error[0] = fabs(y_temp-y_temp2);
            //std::cout<

结果分析

与直接的多项式插值法结果比较，其速度更快，在阶数相同时保持一致的误差，并且随着插值点数的增加，误差还可以进一步减小，对于测试函数$\sqrt{x+3}$其龙格现象没那么明显。

误差分析

为了评估插值函数在计算某个x时的误差，计$R_n(x)=f(x)-L_n(x)$，可以得到$R_n(x)=\frac{f^{(n+1)({\xi }_x)}}{(n+1)!}{\prod }_{i=0}^n(x-x_i)(\min (x_0,x_1,\cdots x_n)\le \xi \le \max (x_0,x_1,\cdots x_n))$，但是用插值函数的时候，意味着原函数在特定的平台较难计算，因此为了方便估计这个误差，使用事后估计法：设$L_n(x)$为$f(x)$以$x_0,x_1,\cdots x_n$为节点的插值多项式，另外取一个节点$x_{n+1}$，记$L_n^{(1)}(x)$为$f(x)$以$x_1,x_2\cdots x_n,x_{n+1}$为节点的插值多项式，则有
$$f(x)-L_n(x)=\frac{f^{(n+1)({\xi }_1)}}{(n+1)!}\prod _{i=0}^n(x-x_i)$$
$$f(x)-L_n^{(1)}(x)=\frac{f^{(n+1)({\xi }_2)}}{(n+1)!}\prod _{i=1}^{n+1}(x-x_i)$$
由于$f^{(n+1)}(x)$在插值区间上变化不大，因此可以认为$$\frac{f(x)-L_n(x)}{f(x)-L_n^{(1)}(x)}\approx \frac{x-x_0}{x-x_{n+1}}$$
转化一下可以得到
$$f(x)-L_n(x)\approx \frac{x-x_0}{x_{n+1}-x_0}(L_n(x)-L_n^{(1)}(x))$$

这个估计误差的方法就被称为时候估计法，当需要计算某次插值的计算误差时，就可以直接使用该方法进行误差估计。